博弈总结及证明
博弈论
博弈论又被称为对策论(Game Theory),既是现代数学的一个新分支,也是运筹学的一个重要学科。 博弈论主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。
——360百科
巴什博弈
在一个风和日丽的下午,甲熊猫头对乙熊猫头说:

乙熊猫头回应:

规则如下:
有一堆石子,假设有n个,二熊猫轮流从这对石子中拿走一定数量的石子(最少1个,最多m个),最后一次操作的玩家获胜。
这个游戏看似杂乱,但是实际蕴含着深刻的数学原理。
由规则可以想到必胜的状态:甲熊猫,拿完石子之后,剩余m+1个石子,那么乙熊猫怎么取都不会获胜,并且在乙熊猫做完这次操作之后,甲熊猫一定能拿走剩余所有的石子,继而获胜。
这样貌似找到了必胜的状态:
总石子的个数n 表示为
(m + 1) * k + r , (k = 1,2,3,4,…., 0 <= r < m + 1)
如果r == 0, 那么先手拿了x个石子,后手只需要拿走m + 1 – x 个石子保证剩余石子是m + 1的倍数,那么就会出现必胜态,从而后手一定能获胜。
如果r != 0,那么先手拿走r个石子,后手拿走x个石子,轮到先手再拿的时候,只需要拿走m + 1 – x个石子,保证剩余石子是m + 1的倍数,就会出现必胜态,从而先手一定能获胜。
威佐夫博弈
规则
有两堆石子,各有n和m块石子,双方轮流取石子,每次操作:
- 从其中一堆石子中取若干(最少1个)
- 从两堆石子取相同个数的若干(最少1个)
最后一次操作的一方获胜。
用(a, b)表示一个操作的状态,显然当一方面临(0,0),此时是必败态。在平面直角坐标系上,首先标出(0,0)是必败态,那么(0,k)(k,0)(k,k)就是必胜态,同时(1,k),(k,2),(1+k,2+k)…均为必胜态,如下图。
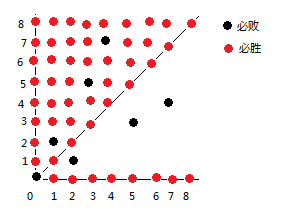
通过上图可以发现必败态为(0,0)(1,2)(3,5)(4,7)(6,10)….,定义此问题中的必败态为“奇异局势”,可以想到的必败态:(0,0)为必败态,第k个必败态的|a – b|必定为k,已知前k个必败态,那么第k+1个必败态的的第一个数为,前k个必败态中没出现过的最小数。
奇异局势的三个性质:
- 任何自然数都包含在一个且仅有一个奇异局势中
- 任意操作都可将奇异局势变为非奇异局势
- 采用适当的方法,可以将非奇异局势变为奇异局势
给定状态,如何判断是否为“奇异局势”?
Beatty定理
设α、β是正无理数且 1/α +1/β =1。记P={ [na] | n为任意的正整数},Q={ [nβ] | n 为任意的正整数},([x]'指的是取x的整数部分)则P与Q是Z+的一个划分,即P∩Q为空集且P∪Q为正整数集合N+。
——360百科
“奇异局势“是贝蒂定理的特例,通过构造“奇异局势”的通项(x, y),继而判断。
设an = [n *α]
bn = [n * b]
贝蒂定理满足“奇异局势”的性质:1.递增,2.任何一个自然数只会在(an, bn)中出现一次。所以只需要构造出|an – bn| = n即可,即a + 1 = b
解方程:
1 / a + 1 / (a +1) = 1 得 a = (sqrt(5) + 1) / 2 = 1.618...(黄金分割数)
结论:当处于“奇异局势”时,先手必败,否则先手必胜。
如何判断是否处于“奇异局势”:当ak=[k(1+sqrt(5))2] 判断bk是否等于ak+k。
尼姆博弈
规则:有三堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
假设有两个人A,B,并且有若干堆物品,A先手,是A必胜,还是B必胜,必胜的策略是什么?
为了更容易的理解,现在考虑一种特殊情况,如果只有两堆物品,如果两堆物品相同的话,A先从一堆中取走x个物品,那么B只需要从另一堆中同样取走x个物品保证两堆物品的数量相同,那么这样就能保证B获得最后的胜利,这样就得到必胜的策略,保证每堆物品的数量是相同的。
这种2-堆的NIM博弈,也可以扩展到k-堆的NIM博弈中,任意一个数都可以表示成n个二进制的加和,例如 57=2^0+2^3+2^4+2^5,我们可以将这堆物品(57个)是有2^0个,2^3个,2^4个,2^5个这些子堆组成的,显然如果最后每种子堆的数量是偶数,那么先手必败,如果是奇数那么先手必胜,这就是如果n堆物品的异或为零,那么每种子堆的数量就是偶数,先手必败,如果不为零,那么每种 子堆的数量就是奇数,先手必胜,到此NIM博弈结论证明完毕。
定理:
设a、b是正无理数且 1/α +1/β =1。记P={ [nα] | n为任意的正整数},Q={ [nβ] | n 为任意的正整数},([x]'指的是取x的整数部分)则P与Q是Z+的一个划分,即P∩Q为空集且P∪Q为正整数集合Z+。
Beatty定理证明:
定理:
设a、b是正无理数且 1/a +1/b =1。记P={ [na] | n为任意的正整数},Q={ [nb] | n 为任意的正整数},([x]'指的是取x的整数部分)则P与Q是Z+的一个划分,即P∩Q为空集且P∪Q为正整数集合Z+。
I.任一个整数至多在集合P或Q中出现一次
因为a、b为正且1/a +1/b=1,则a、b>1,所以对于不同的整数n,[na]各不相同,类似对b有相同的结果。因此任一个整数至多在集合P或Q中出现一次。
II.P∩Q为空集
现证明P∩Q为空集:(反证法)假设k为P∩Q的一个整数,则存在正整数m、n使得[ma]=[nb]=k。即k < ma、nb<k+1,等价地改写不等式为
m/(k+1)< 1/a < m/k及n/(k+1)< 1/b < n/k。相加起来得 (m+n)/(k+1) < 1 < (m+n)/k,即 k < m+n < k+1。这与m、n为整数有矛盾,所以P∩Q为空集。
III.Z+=P∪Q
现证明Z+=P∪Q:已知P∪Q是Z+的子集,剩下来只要证明Z+是P∪Q的子集。(反证法)假设Z+\(P∪Q)有一个元素k,则存在正整数m、n使得[ma]< k <[(m+1)a]、[nb]< k <[(n+1)b]。 由此得ma < k ≦[ (m+1)a]-1<(m+1)a -1(因为a是无理数),类似地有nb < k ≦[ (n+1)b]-1<(n+1)b -1。等价地改写为 m/k < 1/a < (m+1)/(k+1)及n/k < 1/b < (n+1)/(k+1)。两式加起来,得
(m+n)/k < 1 < (m+n+2)/(k+1),即m+n < k < k+1 < m+n+2。这与m, n, k皆为正整数矛盾。





