Surround the Trees（凸包）

Surround the Trees

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 291    Accepted Submission(s): 140

Problem Description

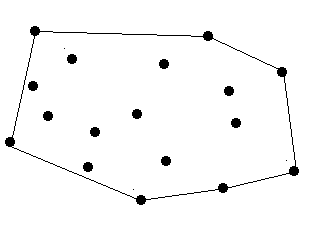
There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him? The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.There are no more than 100 trees.

 

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.

 

Output

            The minimal length of the rope. The precision should be 10^-2.

 

Sample Input

9 
12 7 
24 9 
30 5 
41 9 
80 7 
50 87 
22 9 
45 1 
50 7 
0

 

Sample Output

243.06

 

Source

Asia 1997, Shanghai (Mainland China)

 

Recommend

Ignatius.L

 

 

/*
1,2的时候都需要特判。特别是n==2的时候，是返回1，2之间的距离，而不是返回两倍的距离
*/
#include<bits/stdc++.h>
using namespace std;

const double eps = 1e-8;
const double PI = acos(-1.0);

int sgn(double x)
{
    if(fabs(x) < eps)return 0;
    if(x < 0)return -1;
    else return 1;
}
struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y)
    {
        x = _x;y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    //叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    //点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    void input(){
        scanf("%lf%lf",&x,&y);
    }
};
struct Line { 
    Point s,e; 
    Line(){} 
    Line(Point _s,Point _e) {         
        s = _s; e = _e; 
    }
}; 
//*两点间距离
double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}   
/*
* 求凸包，Graham算法
* 点的编号0~n-1
* 返回凸包结果Stack[0~top-1]为凸包的编号
*/
const int MAXN = 1010;
Point List[MAXN];
int Stack[MAXN],top;
//相对于List[0]的极角排序
bool _cmp(Point p1,Point p2)
{
    double tmp = (p1-List[0])^(p2-List[0]);
    if(sgn(tmp) > 0)
        return true;
    else if(sgn(tmp) == 0 && sgn(dist(p1,List[0]) - dist(p2,List[0])) <= 0)
        return true;
    else 
        return false;
}
void Graham(int n)
{
    Point p0;
    int k = 0;
    p0 = List[0];
    //找最下边的一个点
    for(int i = 1;i < n;i++)
    {
        if( (p0.y > List[i].y) || (p0.y == List[i].y && p0.x > List[i].x) )
        {
            p0 = List[i];
            k = i;
        }
    }
    swap(List[k],List[0]);
    sort(List+1,List+n,_cmp);
    if(n == 1)
    {
        top = 1;
        Stack[0] = 0;
        return;
    }
    if(n == 2)
    {
        top = 2;
        Stack[0] = 0;
        Stack[1] = 1;
        return ;
    }
    Stack[0] = 0;
    Stack[1] = 1;
    top = 2;
    for(int i = 2;i < n;i++)
    {
        while(top > 1 && sgn((List[Stack[top-1]]-List[Stack[top-2]])^(List[i]-List[Stack[top-2]])) <= 0)
            top--;
        Stack[top++] = i;
    }
}   
int n;
int main() {
    //freopen("in.txt","r",stdin);
    while(scanf("%d",&n)!=EOF&&n){
        for(int i=0;i<n;i++){
            List[i].input();
        }
        if(n==1){
            printf("0.00\n");
            continue;
        }else if(n==2){
            printf("%.2lf\n",dist(List[0],List[1]));
            continue;
        }
        Graham(n);
        double cur=0;
        for(int i=0;i<top;i++){
            cur+=dist(List[Stack[i%top]],List[Stack[(i+1)%top]]);
        }
        printf("%.2lf\n",cur);
    }
    return 0;
}