二分匹配总结

二分匹配总结

         首先讲一下什么是二分图，在一个图中，以边为条件，能将两个端点划分为两个集合的图叫做二分图，如下图：

 

       

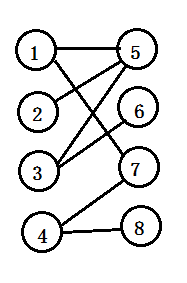
左图为二分图，右图为简化后的二分图。

   

    接着就是二分图的匹配问题，二分图的匹配就是找一个边的集合，每条边的的顶点的度数为1。

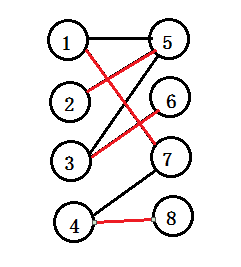
如上图所示，匹配到四条边。

    二分图的完美匹配，就是所有的顶点都有匹配点，这样的叫做完美匹配，上图所示所有的点都有匹配点，所以可以成为完美匹配，并不是所有的图都有完美匹配的。

 

 

讲完了理论部分，那怎么样实现二分图的匹配问题呐，这里就引出了匈牙利算法，匈牙利算法的核心思想就是“能上就上，不能上创造条件也要上”

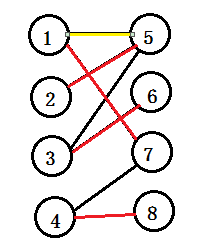
以下图为例：

首先给1号同学找对象，找到了5号；

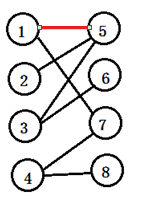
然后再给2号同学找对象，找到了5号，但是5号同学已经有对象了怎么办呐，办法了，只能让5号先跟1号分手，重新给1号找对象，这时候一号的对象就换成了7号，而2号同学就和5号同学在一起了；

接下来就是给3号同学找对象了，找到了5号同学，但是5号同学已经有2号同学了，没办法了，先让2号同学和五号同学分手，刚分手就发现，2号同学除了5号就找不到对象了，所以只能放弃，让3号同学找下一个对象，这样3号同学就找到了，6号同学。

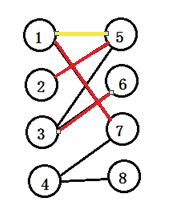
最后就是给4号同学找对象，4号喜欢7号，唉…….这关系我都有点蒙了，多关注一下90后孤独老人，年轻人关系这么复杂……没办法了让7号先和1号分手吧，分手只有又发现问题了，1号又没有对象了，所以还是不能分手，只能让4号重新找对象了，这样4号就找到了8号这样，就完成了，这8个人的匹配问题……

通过代码实现的时候就是利用dfs，给每个人找对象的时候先向上搜索看能不能创造条(fen)件(shou)来进行匹配，如果不能的话只能自己重新找对象了。

/***********************二分匹配模板**************************/
const int MAXN=1000;
int uN,vN;  //u,v数目
int g[MAXN][MAXN];//编号是0~n-1的
int linker[MAXN];//记录匹配点i的匹配点是谁
bool used[MAXN];
bool dfs(int u)//回溯看能不能通过分手来进行匹配
{
    int v;
    for(v=0;v<vN;v++)
        if(g[u][v]&&!used[v])
                  //如果有这条边，并且这条边没有用过
        {
            used[v]=true;
            if(linker[v]==-1||dfs(linker[v]))//如果这个点没有匹配过，并且能找到匹配点，那么就可以以这个边作为匹配点
            {
                linker[v]=u;
                return true;
            }    
        }  
    return false;  
}    
int hungary()//返回最大匹配数
{
    int res=0;
    int u;
    memset(linker,-1,sizeof(linker));
    for(u=0;u<uN;u++)
    {
        memset(used,0,sizeof(used));
        if(dfs(u))//如果这个点有匹配点
                          res++;
    } 
    return res;   
}
/***********************二分匹配模板**************************/