线段树基础详解
线段树是什么?
线段树(Segment Tree)是一种二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
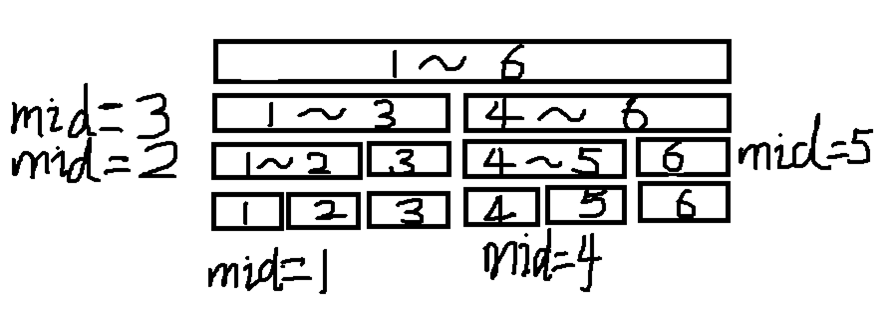
以区间[1,6]的线段树为例
对于每一个非叶子节点区间,取mid=(le+ri)/2;将其分为[le,mid],[mid+1,ri]两个子区间。
如何编号呢?
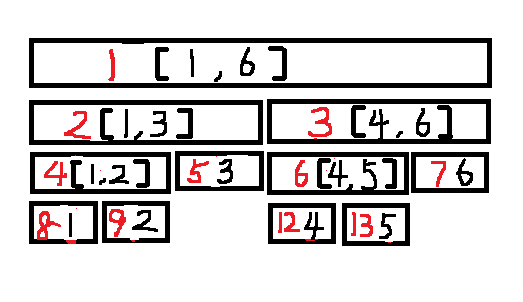
一般根节点可从0或者1开始编号。如果从0开始,则根节点左右子节点的编号分别是1,2.对于某个节点(假设编号为id)
而言,则左右子节点编号分别为id*2+1,id*2+2。如果根节点从1开始,则对于某个节点而言,则左右子节点编号分别为
id*2,id*2+1(我个人喜欢从1开始编号的,从0或1开始都无所谓,注意一下子节点编号就行,我后面所讲都是从1开始编号)。
还是以[1,6]区间编号
线段树有什么用?
线段树特有的性质能够实现快速的查询以及更新等功能( 时间复杂度为O(lg(n)) )。但是线段树不支持删除和插入
(因为一旦多了或少了就会导致整个线段树要重建,那么线段树就没什么用了,还有一种比较高级的数据结构
叫伸展树,既有线段树的优点,还支持插入,删除,翻转等功能,有兴趣自己可以去学)。
以查询区间最大值为例
假设有6个数: 3,1,4,5,7,2. 建立起线段树,区间[1,6],叶子节点分别保存这6个数,非叶子保存它左右儿子中的最大值。
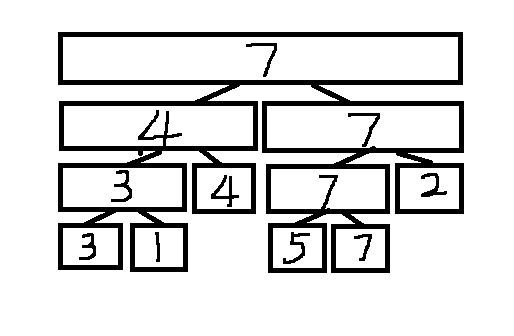
假设我要查询[3,5]的最大值
从根节点开始。根节点区间为[1,6],大了,不完全包含在[3,5]里,所以分成[1,3]和[4,6],[1,3]区间还是大了,
[4,6]同理。再继续分,[1,3]分成[1,2]和[3],[1,2]就不用管了,[3]在区间内,可查询,[4,6]分成[4,5]和[6],
[4,5]在区间内,所以可查询,此时就没必要再分了。[6]不用管。
如何实现呢?
首先是建树(每个人的写法不一样,我给出我的写法,我比较喜欢用结构体把信息封装在一起)
#define e tree[id] //定义成宏,方便 #define lson tree[id*2] #define rson tree[id*2+1] const int maxn=10005; int A[maxn]; struct Tree { int le,ri,v; //左,右,值 }tree[4*maxn]; void pushup(int id){ e.v=max(lson.v,rson.v); } //取左右子节点的最大值 void Build_tree(int id,int le,int ri) { e.le=le,e.ri=ri; if(le==ri){ e.v=A[le]; return; } //区间长度为1 int mid=(le+ri)/2; Build_tree(id*2,le,mid); //左建树 Build_tree(id*2+1,mid+1,ri); //右建树 pushup(id); }
然后就是如何查询
int Query(int id,int x,int y) { int le=e.le,ri=e.ri; if(x<=le&&ri<=y) return e.v; //在区间内,直接返回 int mid=(le+ri)/2; int ret=-INF;// INF是一个非常大的值,自己定义 if(x<=mid) ret=max(ret,Query(id*2,x,y)); //左边可查询 if(y>mid) ret=max(ret,Query(id*2+1,x,y));//右边可查询 return ret; }
单点更新
假如现在我把某个数改变了,那么再查询的时候结果可能就不一样了。如何修改呢?
void Update(int id,int k,int v) //k是修改的位置 { //v是要修改成的值 int le=e.le,ri=e.ri; if(le==ri){ e.v=v; return; } //找到了位置,修改 int mid=(le+ri)/2; if(k<=mid) Update(id*2,k,v); //修改左边 else Update(id*2+1,k,v); //修改右边 pushup(id); //修改过后要记得更新 }
成段更新
前面讲的只是单点更新,如果要更新的是一段区间呢?如果我对这段区间每个点都单点更新一次,貌似可行,
但是时间上肯定爆了。此时你可能会想一个问题,每次成段更新时我还是把那么多个节点都访问了一次,
时间上怎么说都爆了?那么现在就需要一个技巧,延迟更新,这也是线段树这种数据结构特别巧妙的地方。
还是以刚才的例子,不过更新某个值变成给某段区间都加上一个值。此时我还需要在结构体中添加一个变量,
就记为d,代表这段区间需要加上的值(可能现在这样说还是很难理解),d在建树的时候置为0.
void pushdown(int id) { if(e.d!=0&&e.le!=e.ri) //不为0且不是叶子节点需要更新 { //它的左右儿子 lson.v+=e.d; lson.d+=d; rson.v+=e.d; rson.d+=d; e.d=0; //更新完后要置为0,不然以后会重复更新 } } void Update(int id,int x,int y,int d) { int le=e.le,ri=e.ri; if(x<=le&&ri<=y){ e.v+=d; e.d+=d; return; } //在范围内 pushdown(id); //这里就是延迟更新的关键地方 int mid=(le+ri)/2; if(x<=mid) Update(id*2,x,y,d); //左边 if(y>mid) Update(id*2+1,x,y,d);//右边 pushup(id); //每次都需要pushup,因为更新会改变保存的信息 } //在Query时每到一个节点就需要pushdown和pushup(pushup有时可不必, //但pushdown需要,不然查询可能会出错)
给个例题
Poj3468
题意:给出N个数,有两种操作,一种是给一段区间加上一个值,另一种操作是查询一段区间的和。
解析:裸的成段更新的题。详见代码实现。

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<sstream> #include<algorithm> #include<utility> #include<vector> #include<set> #include<map> #include<queue> #include<cmath> #include<iterator> #include<stack> using namespace std; #define e tree[id] #define lson tree[id*2] #define rson tree[id*2+1] typedef __int64 LL; const int INF=1e9+7; const double eps=1e-7; const int maxn=100005; LL A[maxn]; struct Tree { int le,ri; LL sum,d; }tree[4*maxn]; void pushup(int id){ e.sum=lson.sum+rson.sum; }//取其和 void pushdown(int id) //延迟更新 { if(e.d!=0&&e.le!=e.ri) //d不为0且不是叶子节点 { lson.sum+=(lson.ri-lson.le+1)*e.d; //左右儿子的和要加上他们自身的长度乘以d rson.sum+=(rson.ri-rson.le+1)*e.d; lson.d+=e.d; //推到下一层,因为子树还没更新 rson.d+=e.d; e.d=0; //更新完了得置为0,不然会重复更新 } } void Build_tree(int id,int le,int ri) //建树 { e.le=le,e.ri=ri,e.d=0; if(le==ri){ e.sum=A[le]; return; } int mid=(le+ri)/2; Build_tree(id*2,le,mid); Build_tree(id*2+1,mid+1,ri); pushup(id); } void Update(int id,int x,int y,int d) //更新 { int le=e.le,ri=e.ri; if(x<=le&&ri<=y){ e.sum+=(ri-le+1)*d; e.d+=(LL)d; return; } pushdown(id); //推下去 int mid=(le+ri)/2; if(x<=mid) Update(id*2,x,y,d); //更新左边 if(y>mid) Update(id*2+1,x,y,d); //更新右边 pushup(id); //推上去 return; } LL Query(int id,int x,int y) { int le=e.le,ri=e.ri; if(x<=le&&ri<=y) return e.sum; pushdown(id); //这个一定要,不然查询结果会出错 int mid=(le+ri)/2; LL ret=0; if(x<=mid) ret+=Query(id*2,x,y); if(y>mid) ret+=Query(id*2+1,x,y); return ret; } int main() { int N,Q,x,y,d; char op[2]; scanf("%d%d",&N,&Q); for(int i=1;i<=N;i++) scanf("%I64d",&A[i]); Build_tree(1,1,N); while(Q--) { scanf("%s",op); if(op[0]=='C') { scanf("%d%d%d",&x,&y,&d); Update(1,x,y,d); } else { scanf("%d%d",&x,&y); printf("%I64d\n",Query(1,x,y)); } } return 0; }
前面的内容是基础的东西。后面要讲的是加深的内容。
区间覆盖(poj2528)
题意:在一张很大的墙上(长度为10000000),人们在上面贴海报(海报的高度是一样的,长度不一样),会给出每张
海报贴的起始位置和终末位置(注意它给的区间不是像尺子上的刻度),然后问有多少张海报能被看见(有的海报可能被遮住了)。
解析:遇到这类题目,容易想到线段树,但是长度太长,直接开这么大直接爆了,不过N很小,不如先离散化一下。
(有的题目需要离散化后再乘以2,不过这个题目不需要,如果题目给的左右端点是类似刻度那样的就需要,比如有
两段区间[2,4]和[5,100],如果我不乘以2的话[2,100]都会被覆盖,其实[4,5]是空白的),然后就是更新了,每次
更新时把在范围内的全部都改为对应海报的编号,最后整个都查询一遍,可以用set记录有多少种不同的海报编号,
输出答案即可。(详见代码实现,能自己写最好,不过你可以对比一下我的写法)

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<sstream> #include<algorithm> #include<utility> #include<vector> #include<set> #include<map> #include<queue> #include<cmath> #include<iterator> #include<stack> using namespace std; #define e tree[id] #define lson tree[id*2] #define rson tree[id*2+1] const int maxn=10005; int N,L[maxn],R[maxn],A[2*maxn]; struct Tree { int le,ri,d,lazy; }tree[2*4*maxn]; //N有10000,左右两个点,再乘上4倍 void Build_tree(int id,int le,int ri)//建树 { e.le=le,e.ri=ri,e.d=e.lazy=0; //d置为0代表为空白 if(le==ri) return; int mid=(le+ri)/2; Build_tree(id*2,le,mid); Build_tree(id*2+1,mid+1,ri); } void pushdown(int id) { if(e.lazy!=0) //延迟更新 { lson.d=lson.lazy=e.lazy; rson.d=rson.lazy=e.lazy; e.lazy=0; } } void Update(int id,int x,int y,int d) { int le=e.le,ri=e.ri; if(x<=le&&ri<=y){ e.d=e.lazy=d; return; } pushdown(id); int mid=(le+ri)/2; if(x<=mid) Update(id*2,x,y,d); if(y>mid) Update(id*2+1,x,y,d); } int Query(int id,int k) { int le=e.le,ri=e.ri; if(le==ri) return e.d; pushdown(id); int mid=(le+ri)/2; if(k<=mid) return Query(id*2,k); else return Query(id*2+1,k); } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d",&N); int k=0; for(int i=1;i<=N;i++) { scanf("%d%d",&L[i],&R[i]); A[++k]=L[i]; A[++k]=R[i]; } sort(A+1,A+k+1); int Size=1; for(int i=2;i<=k;i++) if(A[i]!=A[Size]) A[++Size]=A[i];//离散化 Build_tree(1,1,Size); //建树 for(int i=1;i<=N;i++) { int x=lower_bound(A+1,A+Size+1,L[i])-A; //找到对应的下标 int y=lower_bound(A+1,A+Size+1,R[i])-A; Update(1,x,y,i); //把[x,y]区间更新为i } set<int> se; for(int i=1;i<=Size;i++) { int x=Query(1,i); if(x!=0) se.insert(x); //不为0代表被覆盖了用集合计算有多少种不同的海报 } printf("%d\n",(int)se.size()); } return 0; }
区间染色(poj1436)
题意:给出N条互斥的垂直x轴的线段。若两个线段之间存在没有其他线段挡着的地方,则称两个线段为可见的。
若3条线段两两互为可见,称为一组,求N条线段中有多少组。
解析:刚开始很难想到用线段树解,这是区间染色问题。先对x坐标排序,每次增加一条边(成段更新) 就和之前的颜色标记起来。
mark[i][j]代表这两条边可见,插入完了之后就是三重循环暴力找,但其实并没有这么多。还有这题的y坐标就需要扩大2倍,
因为是边界问题。(详见代码实现,最好看一下我pushup的写法)

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<sstream> #include<algorithm> #include<utility> #include<vector> #include<set> #include<map> #include<queue> #include<cmath> #include<iterator> #include<stack> using namespace std; #define e tree[id] #define lson tree[id*2] #define rson tree[id*2+1] const int maxn=8002; int N; bool mark[maxn][maxn];//标记i,j两条线段是否能看到 struct Line { int y1,y2,x; //保存一条线段 Line(int y1=0,int y2=0,int x=0):y1(y1),y2(y2),x(x){} bool operator < (const Line& t) const { return x<t.x; } //以x坐标排序 }L[maxn]; struct Tree { int le,ri,c; //c代表被染色的编号 }tree[2*4*maxn]; void Build_tree(int id,int le,int ri) { e.le=le,e.ri=ri,e.c=0; if(le==ri) return; int mid=(le+ri)/2; Build_tree(id*2,le,mid); Build_tree(id*2+1,mid+1,ri); } void pushdown(int id){ if(e.c>0) lson.c=rson.c=e.c; } //左右儿子都被标记为c void pushup(int id) //这种写法是一个技巧,只有当它所包含的整个区间都是 { //同一种颜色时才标记为c,否则为-1 if(lson.c==-1||rson.c==-1) e.c=-1; else if(lson.c!=rson.c) e.c=-1; //左边不等于右边 else e.c=lson.c; } void Query(int id,int x,int y,int c) { int le=e.le,ri=e.ri; if(e.c!=-1) { mark[e.c][c]=mark[c][e.c]=true; return; } pushdown(id); int mid=(le+ri)/2; if(x<=mid) Query(id*2,x,y,c); if(y>mid) Query(id*2+1,x,y,c); pushup(id); } void Update(int id,int x,int y,int c) { int le=e.le,ri=e.ri; if(x<=le&&ri<=y) { e.c=c; return; } pushdown(id); int mid=(le+ri)/2; if(x<=mid) Update(id*2,x,y,c); if(y>mid) Update(id*2+1,x,y,c); pushup(id); } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d",&N); Build_tree(1,1,maxn*2); memset(mark,false,sizeof(mark)); int y1,y2,x; for(int i=1;i<=N;i++) { scanf("%d%d%d",&y1,&y2,&x); L[i]=Line(y1*2,y2*2,x); //扩大两倍 } sort(L+1,L+N+1); for(int i=1;i<=N;i++) { Line& t=L[i]; int y1=t.y1,y2=t.y2; Query(1,y1,y2,i); //先查询有多少条边能看见 Update(1,y1,y2,i); //再插入这条边 } int ans=0; for(int i=1;i<=N;i++) //找3条相互能看见的边 { for(int j=i+1;j<=N;j++) if(mark[i][j]) for(int k=j+1;k<=N;k++) if(mark[i][k]&&mark[j][k]) ans++; } printf("%d\n",ans); } return 0; }
区间合并(poj3667)
题意:有一间旅馆,房间排在一条线上,给出M个操作,有两种操作:
解析:一道经典的线段树区间合并的题目,对于每一个节点,我额外增加4个量:len(该区间长度),
lelen(该区间左边连续的空房间个数),rilen(该区间右边连续的空房间个数),maxlen(该区间最大连续的空房间个数)。
在合并的过程中,如果e.lelen==lson.lelen,则e.lelen+=rson.lelen(说明可以延伸到右边去),
如果e.rilen==rson.len,则e.rilen+=lson.rilen(可以延伸到左边去),
maxlen取lson.maxlen,rson.maxlen,e.lelen,e.rilen以及lson.rilen+rson.lelen中的最大值。
有了这些,不知你是否已经知道如何写了。剩下的我不多说,详见代码实现(仔细想想我pushdown和pushup的写法)。

#include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<iostream> using namespace std; #define e tree[id] #define lson tree[id*2] #define rson tree[id*2+1] const int maxn=50005; int N,M; struct Tree { int le,ri,len; int maxlen,lelen,rilen; void init(int a) { maxlen=a*len; lelen=rilen=maxlen; } }tree[4*maxn]; void build_tree(int le,int ri,int id) { e.le=le; e.ri=ri; e.len=ri-le+1; e.init(1); //刚开始都没有被占 if(le==ri) return; int mid=(le+ri)/2; build_tree(le,mid,id*2); build_tree(mid+1,ri,id*2+1); return; } void pushdown(int id) { if(e.maxlen==e.len||e.maxlen==0) //整个区间要么全空要么全被占 { int a=(e.maxlen==e.len); lson.init(a); rson.init(a); } } void pushup(int id) { e.lelen=lson.lelen; if(e.lelen==lson.len) e.lelen+=rson.lelen; //可以延伸到右边去 e.rilen=rson.rilen; if(e.rilen==rson.len) e.rilen+=lson.rilen; //可以延伸到左边去 e.maxlen=max(lson.maxlen,rson.maxlen); //更新maxlen的值 e.maxlen=max(e.maxlen,max(e.lelen,e.rilen)); e.maxlen=max(e.maxlen,lson.rilen+rson.lelen); } int query(int id,int need) { if(e.maxlen<need) return 0; //最大区间连续长度都小于need,就是无解 if(e.lelen>=need) return e.le; //左边的可行 if(lson.maxlen>=need) return query(id*2,need); //左边的最大连续长度大于等于need if(lson.rilen+rson.lelen>=need) return lson.ri-lson.rilen+1; //两段中间的部分可行 return query(id*2+1,need); //查找右边 } void update(int x,int y,int id,int a) { int le=e.le,ri=e.ri; if(x<=le&&ri<=y){ e.init(a); return; } //更新 pushdown(id); int mid=(le+ri)/2; if(x<=mid) update(x,y,id*2,a); //左边 if(y>mid) update(x,y,id*2+1,a);//右边 pushup(id); } void solve1() { int start; scanf("%d",&start); int ans=query(1,start); //找到有连续房间的最左边的下标 printf("%d\n",ans); if(ans) update(ans,ans+start-1,1,0); //ans不等于0才更新 } void solve2() { int start,skip; scanf("%d%d",&start,&skip); update(start,start+skip-1,1,1); } int main() { cin>>N>>M; build_tree(1,N,1); for(int i=1;i<=M;i++) { int type; scanf("%d",&type); if(type==1) solve1(); else solve2(); } return 0; }







