CodeForces 225C Barcode DP

也是一道dp ,想到了就会觉得很巧妙

矩阵中只有白块和黑块，要求repaint后满足下述条件：

1. 每列一种颜色
2. 根据输入范围x, y 要求条纹宽度在[x, y] 之间

数据范围： n, m, x and y (1 ≤ n, m, x, y ≤ 1000; x ≤ y). 

求：满足条件最少repaint的次数

自己在YY的时候觉得这么大的数据范围肯定没得暴力，估计就dp 了= = 

是可以想出这么个dp 公式: cur[][] = Sigma(x ~ y) Min( former[][] + Sum[] )

不过细节没有想全

看了Tutorial 后顿时明白了

题中只有两种颜色Black 和 White ，先作一个预处理使得可以求出任意posX 到 posY 之间White 和 Black 块的数目

然后就可以开始状态转移了~

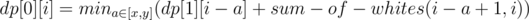
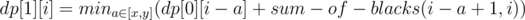
最后的答案就是min(dp[0][m], dp[1][m]).

 

Source Code:

//#pragma comment(linker, "/STACK:16777216") //for c++ Compiler
#include <stdio.h>
#include <iostream>
#include <fstream>
#include <cstring>
#include <cmath>
#include <stack>
#include <string>
#include <map>
#include <set>
#include <list>
#include <queue>
#include <vector>
#include <algorithm>
#define Max(a,b) (((a) > (b)) ? (a) : (b))
#define Min(a,b) (((a) < (b)) ? (a) : (b))
#define Abs(x) (((x) > 0) ? (x) : (-(x)))
#define MOD 1000000007
#define pi acos(-1.0)

using namespace std;

typedef long long           ll      ;
typedef unsigned long long  ull     ;
typedef unsigned int        uint    ;
typedef unsigned char       uchar   ;

template<class T> inline void checkmin(T &a,T b){if(a>b) a=b;}
template<class T> inline void checkmax(T &a,T b){if(a<b) a=b;}

const double eps = 1e-7      ;
const int N = 1              ;
const int M = 200000         ;
const ll P = 10000000097ll   ;
const int INF = 0x3f3f3f3f   ;

char a[1100][1100];
int v1[1100][2], v2[1100][2];
int dp[2][1100];

int main(){
    int i, j, k, t, n, m, numCase = 0;
    int x, y;
    while(cin >> n >> m >> x >> y){
        memset(v1, 0, sizeof(v1));
        for(i = 1; i <= n; ++i){
            for(j = 1; j <= m; ++j){
                cin >> a[i][j];
                if('#' == a[i][j])  ++v1[j][1];
                else    ++v1[j][0];
            }
        }
        v2[1][0] = v1[1][0];
        v2[1][1] = v1[1][1];
        for(i = 2; i <= m; ++i){
            v2[i][0] = v2[i - 1][0] + v1[i][0];
            v2[i][1] = v2[i - 1][1] + v1[i][1];
        }
        memset(dp, 0x3f, sizeof(dp));
        dp[0][0] = dp[1][0] = 0;
        for(j = 1; j <= m; ++j){
            for(int a = x; a <= y; ++a){
                if(j - a < 0)   break;
                checkmin(dp[0][j], dp[1][j - a] + v2[j][0] - v2[j - a][0]);
                checkmin(dp[1][j], dp[0][j - a] + v2[j][1] - v2[j - a][1]);
            }
        }
        cout << Min(dp[0][m], dp[1][m]) << endl;

    }

    return 0;
}