树链剖分
树链剖分是一种对树进行划分的算法,将树分为多条链子,保证每个点只属于一条链,然后再通过数据结构(数组数组,BST,SPLAY,线段树等)来维护每一条链。
一般解决如下问题:
1.将树从x到y结点最短路径上所有的结点的数值都加上c
2.求树从x到y结点最短路径上所有节点的值之和
3.将以x为根节点的子树内所有节点值都加上z
4.求以x为根节点的子树内所有节点值之和
主要概念:
重儿子:在该节点的儿子中,子数数量最多的节点(如果存在多个最大的,选其一即可)(叶子节点无重儿子)
轻儿子:在该节点的儿子中,除重儿子之外的节点
重边:节点和其重儿子连成的边
轻边:节点和其轻儿子连成的边
重链:多条重边连成的路径
轻链:多条轻边连成的路径
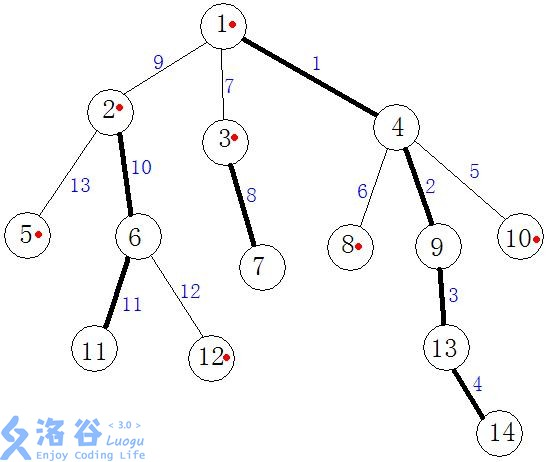
如上图,1的重儿子是4,因为4有三棵子树。而2的重儿子是6。
而上图粗体黑线就是重链或者重边了。
基本的操作方法
1.在把所有的点连成树后我们先计算出每个点的父亲节点,深度,子树的数量,重儿子
2.完成第一步后我们将节点及其重儿子,重儿子的重儿子(重重儿子)等等连接成一条重链。通过这样的操作将树分成一条一条的重链
3.在重链上或者重链与重链之间进行具体的操作
1,2两步可以用两个dfs来完成
第一个dfs求出节点的子树数量(size),节点在树中的深度(deep),节点的父亲节点(fa),节点的重儿子(son)
int size[maxn],deep[maxn],fa[maxn],son[maxn];
void dfs1(int u,int f,int dep){ // u代表节点,f代表父亲,dep代表深度
size[u]=1;
deep[u]=dep;
fa[u]=f;
for(int i=head[u];i;i=tree[i].next){
int v=tree[i].to; //u的儿子
if(v==fa[u]) continue;
dfs1(v,u,dep+1); //遍历儿子,遍历完之后就可以得到v的子树数量
size[u]+=size[tree[i].to];
if(size[tree[i].to]>size[son[u]]) //如果v的子树数量大于u原来重儿子的子树数量,v就是u的重儿子
son[u]=tree[i].to;
}
}
第一次dfs之后的节点情况如图

而第二次dfs则是求出每个节点所在的重链上的起始重儿子是谁,节点是第几次被dfs到的(dfs序),dfs序所对应的节点。
int tim,top[maxn],tid[maxn],rank[maxn];
//top 节点所在重链上的起始重儿子
//tid 节点的dfs序列
//rank dfs序对应的节点
void dfs2(int u,int t){ // u代表节点 ,t代表u所在重链的根部
top[u]=t;
tid[u]=++tim;
rank[tim]=u;
if(son[u]==-1) return ;
else dfs2(son[u],t); //将该点的重儿子,重重儿子,重重重儿子等等连成一条重链
for(int i=head[u];i;i=tree[i].next){
int c=tree[i].to;
if(v!=fa[u]&&v!=son[u]) //如果v不是u的重儿子,就构造新的重链
dfs2(v,v);
}
}
第二个dfs之后每个节点的情况
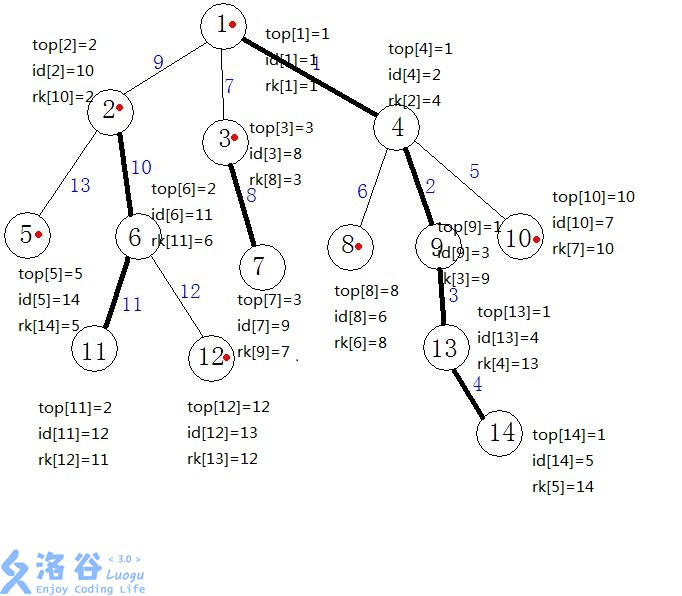
两次dfs之后根据第二次dfs求出的新编号建立线段树
void build(int l,int r,int rt){
lazy[rt]=0;
if(l==r){
sum[rt]=a[rank[l]]; //根据dfs序来建树而不是 sum[rt]=a[l];
return ;
}
int mid=(l+r)<<1;
build(ls);
build(rs);
pushup(rt);
}
求解题目:
给定一棵树,改变x到y最短路径上的所有值。
思路:我们只需将两个节点移动到同一重链上并更新每次移动,在每次移动中都是移动起始重儿子深度更深的节点。

将x到节点y最短路径上所有节点的值增加z
假设x=7,y=13
先比较deep[top[7]]与deep[top[13]]的大小,7的更大,所以先更新区间(tid[top[7]],tid[7]),再令x=fa[top[7]],这时x就是节点1.
这时x=1,y=13,x和y便处于同一重链,最后再进行一次更新,更新区间(tid[1],tid[13])。
void update1(int x,int y,int c){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y); //深度大的先修改
update(tid[top[x]],tid[x],c,1,N,1);
x=fa[top[x]];
}
if(deep[x]<deep[y]) swap(x,y);
update(tid[y],tid[x],c,1,n,1);
}
而对于更新子树的操作,由第二次dfs可知以x为根节点的子树中,所有节点的dfs序是连续的,所以对子树的修改只需修改区间(tid[x],tid[x]+size[x]-1) 的值,也就是
update(tid[x],tid[x]+size[x]-1,c,1,n,1);
树链剖分有两个性质:
1.轻边(U,V),size(V)<=size(U)/2。
2.从根到某一点的路径上,不超过logN条轻边,不超过logN条重路径。
时间复杂度是O(nlog²n)。
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
说明
时空限制:1s,128M
数据规模:
对于30%的数据: N \leq 10, M \leq 10N≤10,M≤10
对于70%的数据: N \leq {10}^3, M \leq {10}^3N≤103,M≤103
对于100%的数据: N \leq {10}^5, M \leq {10}^5N≤105,M≤105
模板
#include<iostream>
#include<algorithm>
#include<cstring>
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
#define ll long long int
#define ls l,mid,rt<<1
#define rs mid+1,r,rt<<1|1
int N,M,R,P,cnt,head[maxn<<1];
using namespace std;
struct edge{
int to,next;
}e[maxn<<1];
void add(int x,int y){
e[++cnt].to=y;
e[cnt].next=head[x];
head[x]=cnt;
}
int size[maxn],deep[maxn],fa[maxn],son[maxn];
void dfs1(int u,int f,int dep){
size[u]=1;
deep[u]=dep;
fa[u]=f;
for(int i=head[u];i;i=e[i].next){
if(e[i].to==fa[u]) continue;
dfs1(e[i].to,u,dep+1);
size[u]+=size[e[i].to];
if(size[e[i].to]>size[son[u]])
son[u]=e[i].to;
}
}
int tim,top[maxn],tid[maxn],rank[maxn];
void dfs2(int u,int t){
top[u]=t;
tid[u]=++tim;
rank[tim]=u;
if(son[u]==-1) return ;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].next){
if(e[i].to!=fa[u]&&e[i].to!=son[u])
dfs2(e[i].to,e[i].to);
}
}
ll sum[maxn<<2],lazy[maxn<<2],a[maxn];
void pushup(int rt){
sum[rt]=(sum[rt<<1]+sum[rt<<1|1])%P;
}
void build(int l,int r,int rt){
if(l==r){
sum[rt]=a[rank[l]]%P;
return ;
}
int mid=(l+r)/2;
build(ls);
build(rs);
pushup(rt);
}
void pushdown(int rt,int ln,int rn){
if(lazy[rt]){
lazy[rt<<1]=(lazy[rt<<1]+lazy[rt])%P;
lazy[rt<<1|1]=(lazy[rt<<1|1]+lazy[rt])%P;
sum[rt<<1]=(sum[rt<<1]+lazy[rt]*ln%P)%P;
sum[rt<<1|1]=(sum[rt<<1|1]+lazy[rt]*rn%P)%P;
lazy[rt]=0;
}
}
void update(int L,int R,int c,int l,int r,int rt){
if(L<=l&&R>=r){
sum[rt]+=c*(r-l+1);
lazy[rt]+=c;
return ;
}
int mid=(l+r)/2;
pushdown(rt,mid-l+1,r-mid);
if(L<=mid) update(L,R,c,l,mid,rt<<1);
if(R>mid) update(L,R,c,mid+1,r,rt<<1|1);
pushup(rt);
}
ll query(int L,int R,int l,int r,int rt){
if(L<=l&R>=r) return sum[rt];
int mid=(l+r)/2;
pushdown(rt,mid-l+1,r-mid);
ll ans=0;
if(L<=mid) ans=(ans+query(L,R,ls)%P)%P;
if(R>mid) ans=(ans+query(L,R,rs)%P)%P;
return ans%P;
}
void update1(int x,int y,int c){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
update(tid[top[x]],tid[x],c,1,N,1);
x=fa[top[x]];
}
if(deep[x]<deep[y]) swap(x,y);
update(tid[y],tid[x],c,1,N,1);
}
ll query1(int x,int y){
ll ans=0;
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]) swap(x,y);
ans=(ans+query(tid[top[x]],tid[x],1,N,1)%P)%P;
x=fa[top[x]];
}
if(deep[x]<deep[y]) swap(x,y);
ans+=query(tid[y],tid[x],1,N,1)%P;
return ans%P;
}
int main(){
cin>>N>>M>>R>>P;
for(int i=0;i<=N;i++){
son[i]=-1;
}
for(int i=1;i<=N;i++)
cin>>a[i];
int x,y;
for(int i=1;i<N;i++){
cin>>x>>y;
add(x,y);
add(y,x);
}
dfs1(R,0,1);
dfs2(R,R);
build(1,N,1);
int op,z;
for(int i=1;i<=M;i++){
cin>>op;
if(op==1){
cin>>x>>y>>z;
update1(x,y,z);
}
if(op==2){
cin>>x>>y;
cout<<query1(x,y)<<endl;
}
if(op==3){
cin>>x>>z;
update(tid[x],tid[x]+size[x]-1,z,1,N,1);
}
if(op==4){
cin>>x;
cout<<query(tid[x],tid[x]+size[x]-1,1,N,1)%P<<endl;
}
}
return 0;
}


