数学基础-概率论04(统计推断-参数假设检验)
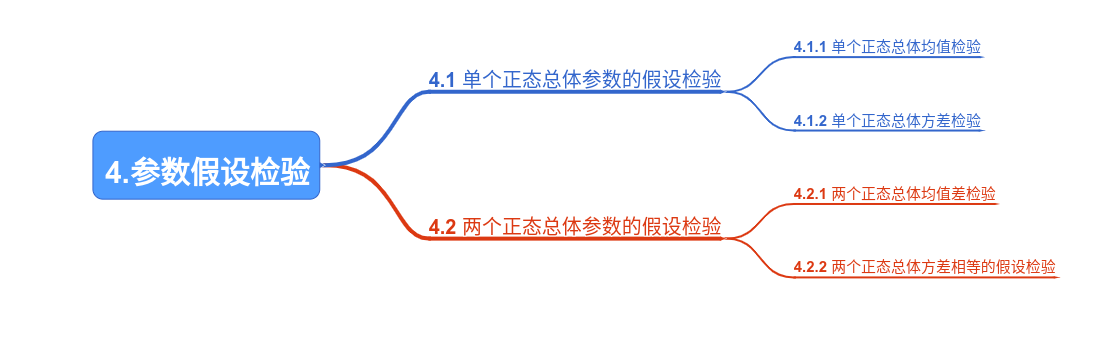
4.参数假设检验
统计推断的另一类重要的问题是假设检验,所谓假设检验就是对总体分布中的某个参数或者分布的形式作出某种假设,利用抽取样本提供的信息,构造适合的统计量,再根据小概率事件进行检验,以作出统计推断。
常用的假设检验方法有U检验法,t检验法,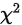 检验法,F检验法
检验法,F检验法
名词解释:
原假设与备择假设:把检验的假设称为原假设;把原假设的对立面称为备择假设
显著性检验与显著性水平:假设检验有两类错误,分别是: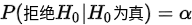 和
和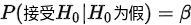 ,通常显示
,通常显示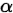 的最大上界而不考虑
的最大上界而不考虑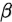 的问题称为假设检验,并将
的问题称为假设检验,并将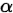 的最大上界称为假设检验的显著性水平。
的最大上界称为假设检验的显著性水平。
双侧边假设检验与单侧边假设检验:针对原假设的假设形式而言,具体查资料,不详细说明。
拒绝域与临界点:拒绝域是统计量的范围,临界点是拒绝域的边界。
假设检验一般步骤:
(1)提出假设:提出原假设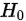 和备择假设
和备择假设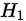
(2)建立合适的统计量,选择检验统计量并确定其分布
(3)确定拒绝域:现给定的显著性水平下,确定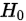 关于统计量的拒绝域
关于统计量的拒绝域
(4)计算:计算样本点对于统计量的值
(5)判断:若统计量落在拒绝域内,则拒绝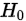 ,否则接受
,否则接受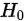
假设检验原理图示:
先来看看前一章参数估计的套路:
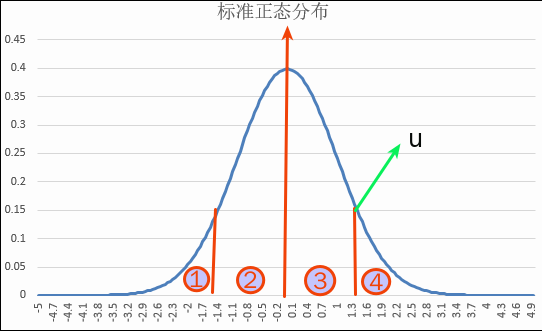
对于给定的置信度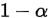 ,我们算得统计量
,我们算得统计量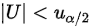 ,并由此得出未知参数的置信区间。图中的2加3为置信区间。
,并由此得出未知参数的置信区间。图中的2加3为置信区间。
对于假设检验,给定显著性水平(即为置信区间中的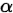 ),构造统计量后,代入具体一次抽样的数据和
),构造统计量后,代入具体一次抽样的数据和假设条件,如果统计量的值在图中2加3的区域下,说明该次抽样是发生在大概率的条件下,则接受假设条件,否则统计量落在3加4的区域内,拒绝假设条件。通常3加4区域为拒绝域,1加2为接受域,依据统计量落的范围决定接受/拒绝假设条件。
4.1 单个正态总体参数的假设检验
4.1.1 单个正态总体均值检验
(1)方差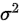 已知
已知
当方差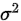 已知,给定显著性水平
已知,给定显著性水平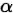 ,假设
,假设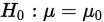 ,其拒绝域为:
,其拒绝域为:
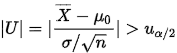
其中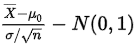 ,
,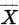 和
和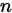 来自样本,
来自样本,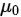 是假设。
是假设。
所以说,上面统计量在某个抽样和假设下的值是可以算出来的,如果该值满足上面的式子(即落在拒绝域内),则拒绝假设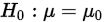
例子:
检验牛奶是否加水,牛奶冰点温度近似满足正态分布,加水会导致该冰点温度升高,其均值方差分别为-0.545和0.008,现抽样5批牛奶,得到均值为-0.534,问这批牛奶是否加水,取显著性水平为0.05.
首先提出假设:
已知统计量为:
已知拒绝域为:
依据抽样数据和假设条件可算得统计量值,即统计量落在拒绝域内,所以拒绝
,即认为牛奶加水了。
注:这种利用标准正态分布的统计量进行检验的方法称为:U检验法
(2)方差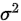 未知
未知
在方差未知的情况下,使用样本的方差进行分析,可构造其统计量为:
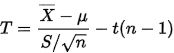
拒绝域为:
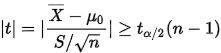
例子
工业废水中,某有害物质含量不超过0.5,现抽样5次,其结果为:0.53,0.542,0.51,0.495,0.515,问抽样结果能说明该废水该有害物质含量是否超标,取显著性水平为0.1
首先提出假设:
已知统计量为:
已知拒绝域为:如果是双边假设检验是:,但是该问题是单边的假设检验,只需要考虑正值的一边,查t分布可知,在正值一边的临界点是
依据抽样数据和假设条件可算得统计量值,即统计量落在拒绝域内,所以拒绝
,即认为有害物质超标。
注:这种利用t分布的统计量进行检验的方法称为:t检验法
4.1.2 单个正态总体方差检验
设X-N(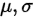 ),抽样一组数据,得到其均值和方差为
),抽样一组数据,得到其均值和方差为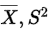 ,有以下假设:
,有以下假设:
$$
原假设: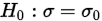 ; 备择假设:
; 备择假设: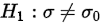 ,其中
,其中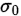 为已知常数。
为已知常数。
可知:
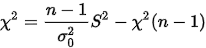
给定显著性水平\alpha,得到以下拒绝域:
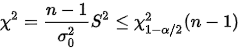
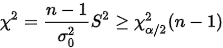
例子:
已知纺纱厂的支数满足正态分布,某种细纱的标准差为1.2,现抽样16个样本,测的其中的标准差为2.1,问该批次细纱较平时均匀度有无变化?取显著性水平为0.05
解:
提出假设: 原假设:; 备择假设:
拒绝域为:或
样本的统计量值为:>样本统计量值在拒绝域内,即拒绝原假设,认为
该批次细纱较平时均匀度有显著性变化。
4.2 两个正态总体参数的假设检验
4.2.1 两个正态总体均值差检验
(1)方差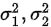 已知
已知
提出假设: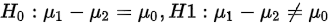 ,其中
,其中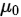 已知
已知
当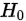 为真时:
为真时:
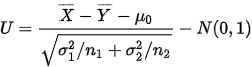
给定显著性水平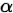 ,拒绝域为:
,拒绝域为:
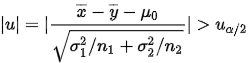
(2)方差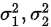 已知,并且
已知,并且
提出假设: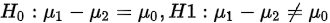 ,其中
,其中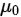 已知
已知
当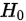 为真时:
为真时:
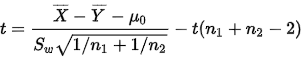
给定显著性水平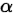 ,拒绝域为:
,拒绝域为:
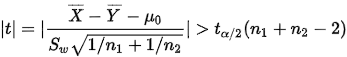
4.2.2 两个正态总体方差相等的假设检验
假设有 两个正态分布,从其中各抽样一次,算得样本方差为
两个正态分布,从其中各抽样一次,算得样本方差为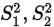
提出假设: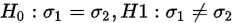
当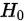 为真时:
为真时:
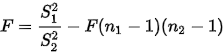
给定显著性水平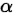 ,拒绝域为:
,拒绝域为:
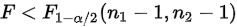 或
或 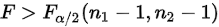
说明
本教程是在学习书籍新编概率论与数理统计-孙淑娥基础上所写的。

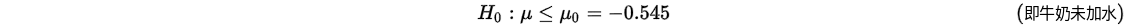
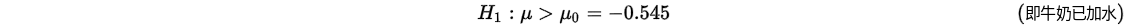
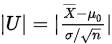
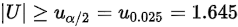
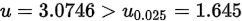
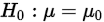
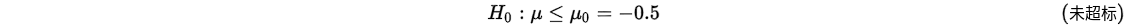
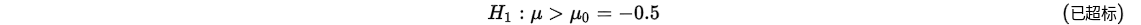
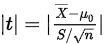
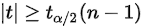
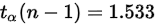
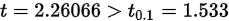
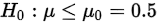
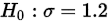
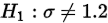
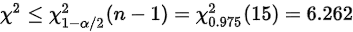
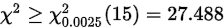
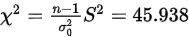

 浙公网安备 33010602011771号
浙公网安备 33010602011771号