数学基础-概率论03(统计推断-参数估计)
目录:

统计推断是通过样本推断总体的分布或者分布的数字特征。
3.参数估计
已知一个总体的分布类型,但是对分布里面的参数不清楚,如泊松分布P( ),正态分布的N(
),正态分布的N(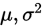 ),这时候需要对这些未知参数进行估计。
),这时候需要对这些未知参数进行估计。
3.1 点估计
点估计:以某个适当的统计量的估测值作为未知参数的估计值
3.1.1 矩估计
矩估计法是用样本n阶矩去估计总体n阶矩,n的大小由未知参数决定,在估计的过程中,解得未知参数。
例子:
1.泊松分布矩估计:已知总体X~P( )[泊松分布],现有样本
)[泊松分布],现有样本 ,求
,求 的矩估计量。
的矩估计量。
首先只有一个未知参数,一阶矩(期望)可以解决,泊松分布的一阶矩为:
其次样本的一阶矩是
令总体的一阶矩等于样本的一阶矩,即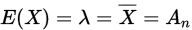 ,解得
,解得 估计量(记为
估计量(记为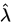 )为:
)为:
2.正态分布矩估计:已知总体X~N(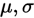 )[正态分布],现有样本
)[正态分布],现有样本 ,求
,求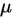 和
和 的矩估计量。
的矩估计量。
两个未知参数,用一阶原点矩和二阶原点矩解决。并使总体的相应矩等于样本矩,建立其方程组后,解出两个参数。
解得: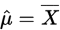 和
和
特点:
1.矩估计的方法依赖于抽取的样本,不同的样本对应不同的参数估计值,所以具有一定随意性
2.使用矩估计要求总体存在原点矩,有些随机变量(如柯西分布)的原点矩不存在,因此无法使用矩估计
3.1.2 极大似然估计
极大似然估计始于高斯误差理论,直观的想法是目前为止所观测到的事件是最有可能出现的事件。比如你和职业车手比赛,有一人赢了,我们总是倾向于是职业车手赢得比赛。
设总体含有待估计参数 ,他可以取很多值,在这很多值值中取出 使得样本出现 的概率最大的那些值,称这些值
,他可以取很多值,在这很多值值中取出 使得样本出现 的概率最大的那些值,称这些值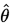 为
为 的极大似然估计。
的极大似然估计。
例子:
1.泊松分布极大似然估计:已知总体X~P( )[泊松分布],现有样本
)[泊松分布],现有样本 ,求
,求 的极大似然估计值。
的极大似然估计值。
已知泊松分布的分布律为:
首先得到似然方程,该批次观测值出现的概率为所以事件的概率乘积,即

取对数得:

由于L和lnL在同一个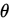 有极值,因此为了求L的极值,可以对lnL使用极限的思想进行分析。
有极值,因此为了求L的极值,可以对lnL使用极限的思想进行分析。
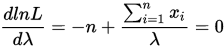
解得 的极大是然估计值(记为
的极大是然估计值(记为 ):
):

特点:
1.不要求总体原点矩存在
2.需要求解似然方程
3.1.3 估计量的评选标准
1.无偏性
假设每次抽样,对参数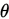 均有一个估计值,记为
均有一个估计值,记为 ,若取所有估计值的期望是对参数的
,若取所有估计值的期望是对参数的 正确无偏估计,即
正确无偏估计,即 ,则
,则 为
为 的无偏估计量。
的无偏估计量。
2.有效性
多次抽样,使用不同的方法计算得到多组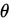 的估计量,这两组中较稳定的(即方差小)较其他组更为有效的估计。方差反映估计值在真实值附近更为“集中”。
的估计量,这两组中较稳定的(即方差小)较其他组更为有效的估计。方差反映估计值在真实值附近更为“集中”。
3.一致性(相合性)
毫无疑问,抽取样本的容量越大,对未知参数的估计越接近真实值,估计量的这种性质称为一致性(相合性)
相合估计量:
设 为未知参数
为未知参数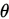 的估计量,若
的估计量,若 依概率收敛于
依概率收敛于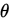 ,则对任意
,则对任意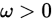 ,有
,有

此时,称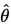 为
为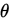 (弱)相合估计量。
(弱)相合估计量。
注:
1.一般而言,三个估计量评选标准只要满足前面两个标准就不错了,因为使用一致性要求样本容量足够大
3.2 区间估计
区间估计:用两个统计量的观测值确定的区间来估计未知参数的大致范围,并给出未知参数落在此区间的概率。
定义
对于事先指定的概率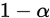 ,若有对未知参数
,若有对未知参数 的统计量
的统计量 和
和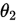 ,使得:
,使得:

那么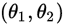 为
为 置信水平为
置信水平为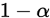 的置信区间,在
的置信区间,在 和
和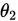 为置信上下限,在
为置信上下限,在 为置信区间长度。
为置信区间长度。
3.2.1 单正态总体参数的区间估计
均值区间估计
(1)总体方差已知,求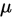 的区间估计
的区间估计
总体服从正态分布且方差 已知时,或者总体不是正态分布但是为大样本时,样本的均值
已知时,或者总体不是正态分布但是为大样本时,样本的均值 的抽样分布均为正态分布,其数学期望为总体的均值
的抽样分布均为正态分布,其数学期望为总体的均值 ,方差为
,方差为 .样本均值经过标准化后的随机变量则服从标准正态分布,即:
.样本均值经过标准化后的随机变量则服从标准正态分布,即:

根据标准正态分布性质,概率密度关于y轴对称,可得到以下式子:
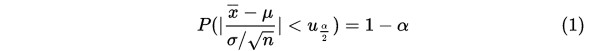
解释如下:
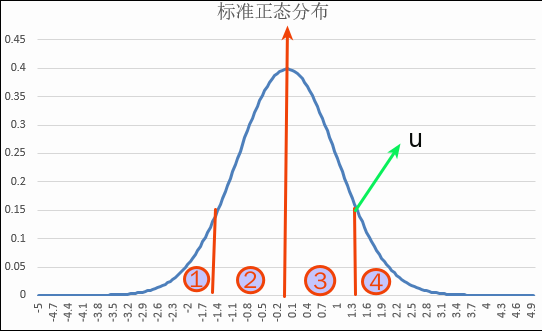
已知概率密度函数下的面积为该变量出现的概率,假设区域2,3的面积和为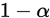 ,则区域1,4的面积和为
,则区域1,4的面积和为 。由于对称关系,1,4各为
。由于对称关系,1,4各为 ,
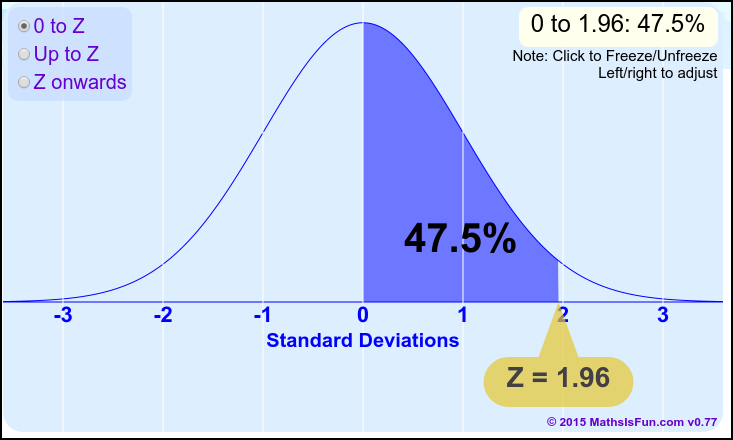
, 为置信度,会提前告知,所以现在是已知概率,要求得随机变量上(即x轴)上对应的位置,如上图的u竖线与x轴的相交点位置。这个只需去查正态分布表。如
为置信度,会提前告知,所以现在是已知概率,要求得随机变量上(即x轴)上对应的位置,如上图的u竖线与x轴的相交点位置。这个只需去查正态分布表。如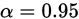 时,
时,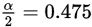 ,去该表中查得总体在(0,
,去该表中查得总体在(0,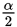 )之间对于的随机变量位置为1.96.
)之间对于的随机变量位置为1.96.
所以,对于公式1, 是根据置信水平
是根据置信水平 确定的,解出不等式为:
确定的,解出不等式为:

所以,置信度为 的总体正态分布的置信区间为
的总体正态分布的置信区间为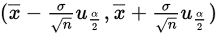
例子:假设随机事件总体满足正态分布N(
,0.05),一次抽样个数n=5,均值为
,求其置信度为98%的置信区间?
解:,查表得
,代入式子得置信区间为
-->表示总体的分布中,未知参数有98%的概率落在区间
.
(2)总体方差未知,求 的区间估计
的区间估计
总体的方差 未知,样本的方差
未知,样本的方差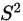 可以作为
可以作为 的无偏估计,构造估计量:
的无偏估计,构造估计量:
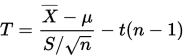
参考连续型概率分布的T分布分析可知:T的概率密度函数的形状类似于均值为0方差为1的正态分布,但更低更宽。所以对于置信度为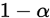 的置信区间为:
的置信区间为:
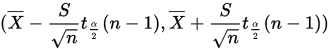
其中 根据n和
根据n和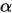 查T分布的临界值表可知。
查T分布的临界值表可知。
3.2.1 双正态总体参数的区间估计
多因素引发质量指标X的变化,若X服从正态分布,则需要对两个正态分布的总体的均值差或方差比给出区间估计。
3.2.1.1 双正态总体均值差的区间估计
a.已知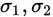
构造统计量:

给定置信水平 ,得以下式子:
,得以下式子:
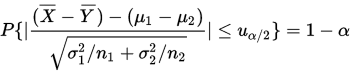
得置信区间为:
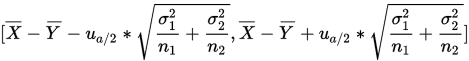
例子:
假设有两批抽样的玩具,其重量如下:
3 6 3 4 5 4
5 6 4 7 8 6
假设这两批样本分别满足正态分布N(,3),N(
,7),求两批样本置信水平为98%的总体重量均值差的区间估计。
解: 由两个样本可知,
,代入置信区间计算式,得置信区间为:
a.未知 ,但是假设
,但是假设
构造统计量:
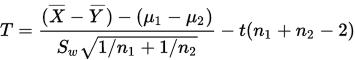
同单总正态参数估计一样,根据t分布的对称性,给出置信水平为 的置信区间为:
的置信区间为:

3.2.1.2 双正态总体方差比的区间估计
构造统计量:

给定置信水平1-\alpha,得:
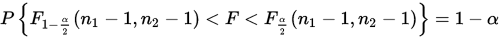
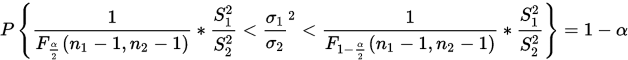
解出区间为:
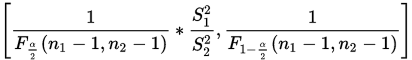
该公式的大部分参数可以通过统计两次抽样得到,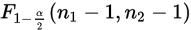 等值查F分布临界值表得到。
等值查F分布临界值表得到。
3.3 (0-1)分布参数的区间估计
设有容量n>50的大样本,它来自(0-1)分布的总体X,Y的分布律为:
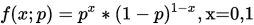
其中p是未知参数,现在求p的置信水平为 的置信区间。
的置信区间。
由于样本量很大,根据中心极限定理得:
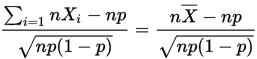
近似满足N(0,1)分布,有式子:

不写具体推导过程了(可参考百度文库),直接写区间估计结果:

其中
例子:
设有一批产品有100个,其中良品60个,求这批产品中置信区间为95%的良品率区间估计。
解: 可知:n=100,
计算得:a=103.84,b=-123.84,c=36,代入式子2,得到:
置信95%的良品率置信区间为**[0.50,0.69]**
说明
本教程是在学习书籍新编概率论与数理统计-孙淑娥基础上所写的。


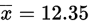






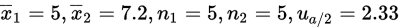

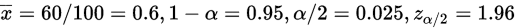

 浙公网安备 33010602011771号
浙公网安备 33010602011771号