数学基础-概率论01(离散型分布)
目录:

1.离散型
1.1 单点分布
单点分布(one-point distribution)亦称一点分布,或称退化分布,是一种最简单的离散型分布。假如随机变量X仅取数值a,即P{X=a}=1,则称随机变量X服从单点分布或退化分布。单点分布的均值E(x)=a,方差Var(x)=0。如果随机变量X有有限均值和零方差,则随机变量X服从单点分布。
概率函数:
$$P(x)= \begin{cases} {1}, & \text {x=a} \\ 0, & \text{x!=a} \end{cases}$$期望值$E(X)=a$;方差 $Var(X)=0$
特点:
该分布下数据衡等于a
1.2 两点分布
两点分布( two-point distribution)即“伯努利分布”或者0-1分布,是一个离散型概率分布。在一次试验中,事件A出现的概率为P,事件A不出现的概率为q=1-p
概率函数:
$$P(x)= \begin{cases} p, & \text {x=a} \\ q, & \text{x=b} \end{cases}$$两点分布的均值$E(X)=pa+qb$,方差$V(X)=pq(a-b)^2$。
特点:
该分布下数据仅有两个可取值,且任意一次随机,取a或b的概率不变
1.3 均匀分布
离散型均匀分布是一个离散型概率分布,其中有限个数值拥有相同的概率,典型的如抛硬币,掷色子
概率密度函数:
$$f(x)= \begin{cases} {\frac 1 {b-a}}, & \text {a< x < b } \\ 0, & \text{else}\end{cases}$$期望:$E(X)=\int_{-\infty}^{\infty} xf(x) dx=\int_{a}^{b} \frac{x}{b-a}dx=\frac{b-a} {2}$
方差:$V(X)=\frac {(b-a)^2} {12}$
特点:
均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值
1.4 二项分布
二项分布就是重复n次独立的伯努利试验,在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。
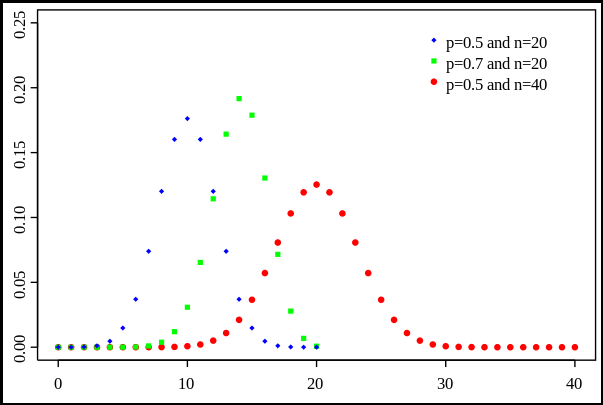
概率函数:
$$P(n,k,p)=C^k_n*p^k(1-p)^{n-k}$$某二项分布。其中p称为成功概率。记作ξ~B(n,p)
期望:$E\xi=np$
方差:$D\xi=np(1-p)$
特点:
1.当p=q时图形是对称的
2.当p≠q时,直方图呈偏态,p<q与p>q的偏斜方向相反。如果n很大,即使p≠q,偏态逐渐降低,最终成正态分布,二项分布的极限分布为正态分布。故当n很大时,二项分布的概率可用正态分布的概率作为近似值。何谓n很大呢?一般规定:当p<q且np≥5,或p>q且nq≥5,这时的n就被认为很大,可以用正态分布的概率作为近似值了
1.5 负二项分布
负二项分布是统计学上一种描述在一系列独立同分布的伯努利试验中,失败次数到达指定次数(记为r)时成功的次数。比如,如果我们定义掷骰子随机变量x值为x=1时为失败,所有x≠1为成功,这时我们反复掷骰子直到1出现3次(失败次数r=3),此时非1数字出现次数的概率分布即为负二项分布。若随机变量X服从参数为r和p的负二项分布,则记为X~NB(r,p).
当r是整数时,负二项分布又称帕斯卡分布(巴斯卡分布)
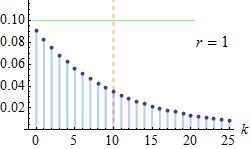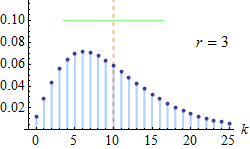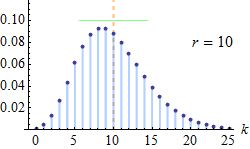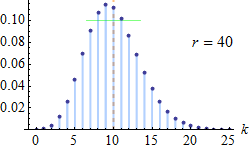
概率密度函数:
$$f(k;r,p)=Pr(x=k)= \begin{pmatrix} k+r-1 \\ k \\ \end{pmatrix}p^k(1-p)^r, \text {k=0,1,2...}$$其中:
$$\begin{pmatrix} k+r-1 \\ k \\ \end{pmatrix}=\frac{(k+r-1)!}{k!(r-1)!}$$期望:$E(X)=\frac{r(1-p)}{p}$
方差:$D(X)=\frac{r(1-p)}{p^2}$
特点:
“负二项分布”与“二项分布”的区别在于:“二项分布”是固定试验总次数N的独立试验中,成功次数k的分布;而“负二项分布”是所有到失败r次时即终止的独立试验中,成功次数k的分布。
1.6 正态分布
又名高斯分布(英语:Gaussian distribution),是一个非常常见的连续概率分布。正态分布在统计学上十分重要,经常用在自然和社会科学来代表一个不明的随机变量。
若随机变量 X 服从一个位置参数为 μ、尺度参数为 σ 的正态分布,记为: $X-N(μ,σ^2)$
概率密度函数:
$$f(x)=\frac{1}{σ \sqrt {2\pi} }e^{- \frac{(x-μ)^2}{2σ^2}}$$期望:$μ$
方差:$σ^2$
说明:
正态分布的数学期望值或期望值 μ 等于位置参数,决定了分布的位置;其方差
$σ^2$的开平方或标准差 σ 等于尺度参数,μ 决定了分布的幅度。
通常所说的标准正态分布是位置参数 μ =0,尺度参数$σ^2$= 1的正态分布.
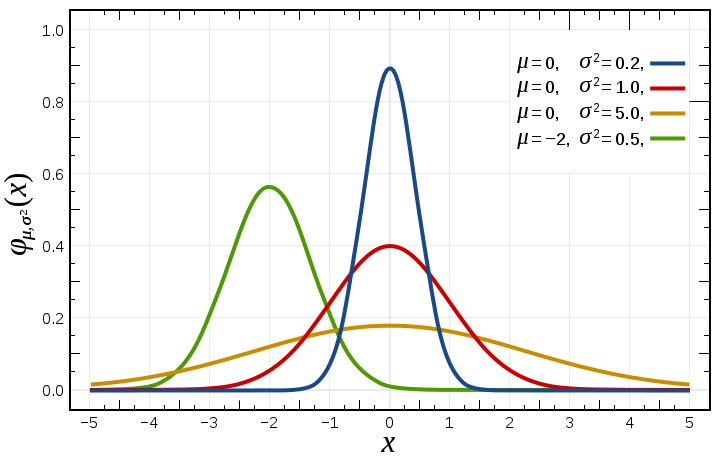
特点:
1.在特定条件下,大量统计独立的随机变量的平均值的分布趋于正态分布,这就是中心极限定理。
2.约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。
1.7 几何分布
几何分布(英语:Geometric distribution)指的是以下两种离散型概率分布中的一种:
在伯努利试验中,得到一次成功所需要的试验次数X。X的值域是{ 1, 2, 3, ... }
在得到第一次成功之前所经历的失败次数Y = X − 1。Y的值域是{ 0, 1, 2, 3, ... }
实际使用中指的是哪一个取决于惯例和使用方便。
如果每次试验的成功概率是p,那么k次试验中,第k次才得到成功的概率是:
$$Pr(X=k)=(1-p)^{k-1}p \tag {k=1,2,3....}$$上式描述的是取得一次成功所需要的试验次数。而另一种形式,也就是第一次成功之前所失败的次数,可以写为:
$$Pr(Y=k)=(1-p)^{k}p \tag {k=0,1,2,3....}$$假设不停地掷骰子,直到得到1。投掷次数是随机分布的,取值范围是无穷集合{ 1, 2, 3, ... },并且是一个p = 1/6的几何分布。
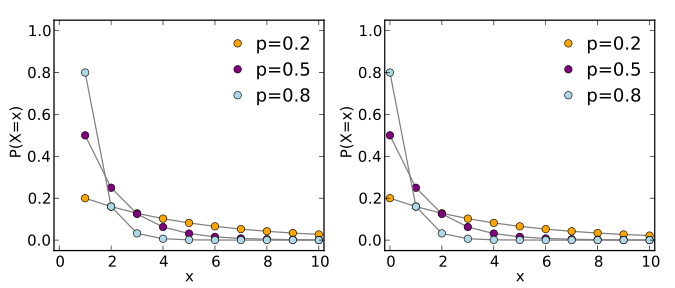
期望与方差:两种不同写法有不同的期望和方差,不在此详细描述,具体可看:
http://www.wikiwand.com/zh-sg/幾何分佈
1.8 超几何分布
超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出n个物件,成功抽出指定种类的物件的个数(不归还 (without replacement)),例如在有N个样本,其中m个是不及格的。超几何分布描述了在该N个样本中抽出n个,其中k个是不及格的机率:
$$f(k;n,m,N)=\frac{C_m^k C_{N-m}^{n-k}}{C_N^n}$$上式可如此理解: $C_N^n$表示所有在N个样本中抽出n个的方法数目。$C_m^k$表示在m个样本中,抽出k个的方法数目,即组合数,又称二项式系数。剩下来的样本都是及格的,而及格的样本有N-m个,剩下的抽法便有$C_{N-m}^{n-k}$种
若n=1,超几何分布还原为伯努利分布,和二项分布不同的是,在超几何分布中,特别强调的是抽出的样品在下一次抽取前不再放回去,但是如果抽取的次数 n和总共样品数 N 相比很小(大约 n / N < 0.05,这时在计算上二项分布和超几何分布相互间则没有主要的区别,此时人们更愿意采用二项分布的方法,因为在数学计算上二项分布要简单一些。
容器中一共10个球,其中6个黑色,4个白色,一共抽5次(抽出的球不放回去),在这5个球中有3个黑球的概率是:
$$f(k=3)=\frac{C_6^3 C_{10-6}^{5-3}}{C_{10}^5}=0.476$$期望:$\frac {nm} N$
方差:$\frac{n(m/N)(1-\frac mN)(N-n)}{N-1}$
1.9 泊松分布
泊松近似是二项分布的一种极限形式。其强调如下的试验前提:一次抽样的概率值 p 相对很小,而抽取次数 n 值又相对很大。因此泊松分布又被称之为罕有事件分布。泊松分布指出,如果随机一次试验出现的概率为 p,那么在 n 次试验中出现 k 次满足泊松分布。
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等.
概率质量函数:
$$P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}$$期望:$\lambda$
方差:$\lambda$
例如,某工厂在生产零件时,每200个成品中会有1个次品,那么在100个零件中最多出现2个次品的概率按照泊松分布应该是:
$$f(100,0,\frac{1}{200})+f(100,1,\frac{1}{200})+f(100,2,\frac{1}{200})=0.986$$参考
https://blog.csdn.net/yan456jie/article/details/52166864
https://wenku.baidu.com/view/4eabd1d180eb6294dd886cbe.html
注:维基百科,百度百科的引用不列举,关键字搜索即可找到。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号