Codeforces Round 917 (Div. 2)

https://codeforces.com/contest/1917

A. Least Product *800

给定整数数组，可以把数组中的数 $a_i$ 改为 $0\sim a_i$ 中的任意整数，最小化所有数的乘积，在此基础上使操作次数最少

讨论一下负数的个数和 $0$ 的个数

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

void sol() {
    int n;
    cin >> n;
    bool zero = 0, neg = 0;
    while (n--) {
        int x; cin >> x;
        if (x < 0) neg ^= 1;
        if (x == 0) zero = true;
    }
    if (zero || neg) cout << "0\n";
    else cout << "1\n1 0\n";
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T; while (T--)
        sol();
}

B. Erase First or Second Letter *1100 还行的思维题

给定字符串，可以删除首字符（即第一个字符）和删除第二个字符任意次，问能得到的本质不同串个数。 $n\le 10^5$

删除后的串长这样（剩下6个字符）：xxxxxx??????

或者这样：xxxxx?xxxxxxxx?????

也就是说长度相同的串只可能在第一个字符处不同

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

void sol() {
    int n;
    string s;
    cin >> n >> s;
    
    int ans = n;
    vector<int> cnt(26);
    for (char c : s) {
        for (int i = 0; i < 26; i++) {
            if (cnt[i] && c - 'a' != i) //前面的一个字符与当前字符不同
                ans++;
        }
        cnt[c - 'a']++;
    }
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T; while (T--)
        sol();
}

C. Watering an Array *1600 比较无聊

有一个长度为$n$的整数数组 $a$，无限循环数组 $b$（$b=[v_1,v_2,\ldots,v_k,v_1,v_2,\ldots,v_k,\ldots]$）。

第 $i$ 次操作你可以执行以下两种操作之一：

• 将数组 $a$ 的前 $b_i$ 个元素的值都加 $1$；
• 计算使 $a_j=j$ 成立的元素个数为 $c$。将 $c$ 加到你的得分上，并将整个数组 $a$ 的所有元素都置为 $0$

求 $d$ 次操作后能获得的最大得分。

$n\le 2000,k\le 10^5, k\le d\le 10^9, 1\le v_i\le n$

我好像非常不擅长这种题。。。居然卡了很久

首次把数组清零后，不管怎么操作数组中的数都单调不增的，所以 $c$ 至多为 $1$。

所以首次把数组清零后，理想的方案是交替进行两种操作，每两次操作使答案 $+1$。

枚举首次清零的时间即可。但是枚举到 $n$ 是不够的！（wa了两发）

可以这样考虑：若交替进行两种操作，则答案增加的速度是 $0.5$。而如果在第 $2n$ 次以后才进行首次操作二，最好的情况是使答案 $+n$，答案增加的平均速度 $<n/2n=0.5$，还不如早点开始交替。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
ll n, k, d, a[N], v[N];
void sol() {
    cin >> n >> k >> d;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= k; i++) cin >> v[i % k];
    
    ll ans = 0;
    for (int i = 1; i <= min(d, n + n); i++) {
        ll res = 0;
        for (int j = 1; j <= n; j++) res += a[j] == j;
        ans = max(ans, res + (d - i) / 2);
        for (int j = 1; j <= v[i % k]; j++) a[j]++;
    }
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T; while (T--)
        sol();
}

D. Yet Another Inversions Problem *2300 挺好的题

给定 $1\sim 2n-1$ 中所有奇数的排列 $p[]$ 和 $0\sim k-1$ 的排列 $q[]$，数组 $a[]$ 定义为：$a_{ik+j}=p_i\cdot 2^{q_j}$，求 $a[]$ 的逆序对数。

$n,k\le 2e5$

$p2^{q_0},p2^{q_1},\cdots ,p2^{q_k}$ 的逆序对数就是排列 $q[]$ 的逆序对数，下文不考虑这种情况。

对于一个数 $p2^{q}$，考虑位置在它之后的哪些数小于它：

• $x2^0,x2^1, \cdots, x2^{q-1}$ $, x\in (p,2p)$
• $x2^0,x2^1, \cdots, x2^{q-2}$ $, x\in (2p,4p)$
• $x2^0,x2^1, \cdots, x2^{q-3}$ $, x\in (4p,8p)$
• $\cdots$

同样还有

• $x2^{0},x2^{1}, \cdots, x2^{q+1}$ $, x\in (p/2,p)$
• $\cdots$

这样复杂度有点高。改为考虑某个 $x\in (p,2p)$ 的贡献：

• $p2^{1}$ 与 $x2^0$ 形成 $1$ 个逆序对
• $p2^{2}$ 与 $x2^0,x2^1$ 形成 $2$ 个逆序对

这样完全可做，但可能不太好写。考虑枚举指数的差：

• 形如 $\{p2^q,x2^{q}\}$ 的逆序对，$x\in(0,p)$，$q$ 有 $k$ 种取值
• 形如 $\{p2^q,x2^{q-1}\}$ 的逆序对，$x\in(0,2p)$，$q$ 有 $k-1$ 种取值
• 形如 $\{p2^q,x2^{q+1}\}$ 的逆序对，$x\in(0,p/2)$，$q$ 有 $k-1$ 种取值

这样好像好写一点点。树状数组维护一下

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int P = 998244353;

struct BIT {
    int n; vector<int> tr;
    BIT(int n): n(n), tr(n + 1) {}
    int lowbit(int x) { return x & -x; }
    void add(int p, int x) { for (; p <= n; p += lowbit(p)) tr[p] += x; }
    int ask(int p) { int s = 0; for (; p > 0; p -= lowbit(p)) s += tr[p]; return s; }
};

void sol() {
    int n, k;
    cin >> n >> k;
    vector<int> p(n), q(k);
    for (int &x : p) cin >> x;
    for (int &x : q) cin >> x;

    ll ans = 0;
    
    //行内逆序对
    BIT row(k);
    for (int i = k - 1; ~i; i--) {
        ans += row.ask(q[i] + 1);
        row.add(q[i] + 1, 1);
    }
    (ans *= n) %= P;
    
    //行间逆序对
    BIT tr(2 * n - 1);
    for (int i = n - 1; ~i; i--) {
        for (ll _k = k, _p = p[i]; _k; _k--, _p *= 2) {
            if (_p >= 2 * n - 1) { //越界了，直接等差数列
                (ans += _k * (_k + 1) / 2 % P * tr.ask(2 * n - 1) % P) %= P;
                break;
            }
            (ans += _k * tr.ask(_p)) %= P;
        }
        for (ll _k = k - 1, _p = p[i] / 2; _k > 0 && _p > 0; _k--, _p /= 2)
            (ans += _k * tr.ask(_p)) %= P;
        tr.add(p[i], 1);
    }
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T; while (T--)
        sol();
}

E. Construct Matrix *2500 构造构造

给定偶数 $n$ 和整数 $k$，构造 $01$ 矩阵，满足：共有 $k$ 个 $1$、每行异或和相等、每列异或和相等。

若无法构造，输出 No

$0\le k \le n^2$

因为每行异或和相等且 $n$ 为偶数，故所有数异或和为 $0$，所以 $k$ 为奇数时无解。下面讨论 $k$ 为偶数的情况：

只有两个 $1$ 或只有两个 $0$，

• $k=2$ 或 $k=n^2-2$，仅当 $n=2$ 时有解

其他情况，

• $k=0,4,8,12,\cdots$，在任意空白处不断填 $2\times 2$ 的全 $1$ 矩阵，每行/列异或和始终是 $0$

• $k=6$，

  1 1 0 0
  1 0 1 0
  0 1 1 0
  0 0 0 0
  

• $k=10,14,18,\cdots$，先把上面的矩阵取反，

  0 0 1 1
  0 1 0 1
  1 0 0 1
  1 1 1 1
  

  然后在旁边加 $2\times 2$ 的全 $1$ 矩阵，即可扩展到 $n$ 为 $\ge k$ 的任意偶数的情况，

  0 0 1 1 1 1
  0 1 0 1 1 1
  1 0 0 1 1 1
  1 1 1 1 1 1
  1 1 1 1 1 1
  

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void sol() {
    int n, k;
    cin >> n >> k;    
    
    bool ok = true;
    vector<vector<int>> a(n + 1, vector<int>(n + 1));
    
    if (k % 2) {
        ok = false;
    } else if (k == 2 || n * n - k == 2) {
        if (n == 2) a[1][1] = a[2][2] = 1;
        else ok = false;
    } else if (k % 4 == 0) {
        for (int i = 1; i <= n; i += 2)
            for (int j = 1; j <= n && k; j += 2)
                a[i][j] = a[i + 1][j] = a[i][j + 1] = a[i + 1][j + 1] = 1, k -= 4;
    } else if (k == 6) {
        for (int i = 1; i <= 3; i++)
            for (int j = 1; j <= 3; j++)
                if (i + j != 4) a[i][j] = 1;
    } else {
        for (int i = 1; i <= 4; i++)
            for (int j = 1; j <= 4; j++)
                if (i + j == 4 || i == 4 || j == 4) a[i][j] = 1;
        k -= 10;
        for (int i = 1; i <= n; i += 2)
            for (int j = 1; j <= n && k; j += 2)
                if (i > 4 || j > 4)
                    a[i][j] = a[i + 1][j] = a[i][j + 1] = a[i + 1][j + 1] = 1, k -= 4;
    }
    
    if (!ok) cout << "No\n";
    else {
        cout << "Yes\n";
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                cout << a[i][j] << " \n"[j == n];
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T; while (T--)
        sol();
}

F. Construct Tree *2500 bitset优化01背包

给定 $n$ 条边的边权，用全部边构造一棵树，要求直径为 $d$

$n\le 2000,d\le 2000$

这种题目一般都是先弄出直径来，然后把其他边挂到某点上。

所有边按从小到大排序，记为 $l_1,l_2,\cdots, l_n$

如果能找出若干条边，边权之和为 $d$，且包含 $l_n$ 在内，那就把它们作为直径，$l_n$ 放在一端，其他的边这样接：

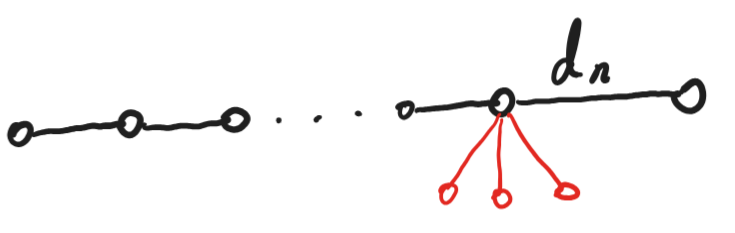
如果 $l_n$ 与某条红边构成直径则无解。实际上，若 $l_n+l_{n-1}> d$ 则无解，因为肯定存在过他们俩的边，使直径 $>d$。

否则如下图这样构造，绿边的边权和小于等于 $l_n$，蓝边的边权和也小于等于 $l_n$，且绿边的边权和加上蓝边的边权和等于 $d$。

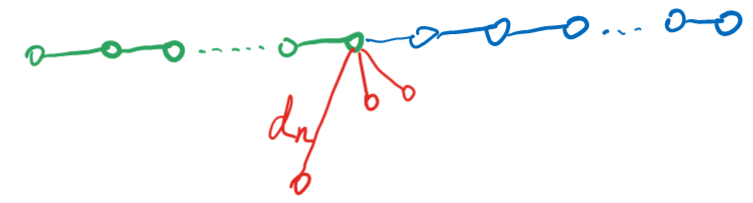
背包，$g[i][j][k]=True/False$ 表示在前 $i$ 条边中选，蓝边的边权和为 $j$，绿边的边权和为 $k$ 是否合法。复杂度 $O(nd^2)$。绝望之中想起bitset优化，复杂度除以 $32$，能过。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2010;
void sol() {
    int n, d;
    cin >> n >> d;
    vector<int> l(n);
    for (int &x : l) cin >> x;
    sort(l.begin(), l.end());
    
    if (l[n - 1] + l[n - 2] > d) return cout << "No\n", void();
    
    bitset<N> f;
    f[0] = 1;
    for (int i = 0; i < n - 1; i++)
        f |= f << l[i];
    if (f[d - l[n - 1]]) return cout << "Yes\n", void();
    
    vector<bitset<N>> g(d + 1);
    g[0][0] = 1;
    for (int i = 0; i < n; i++) {
        for (int j = d; ~j; j--) {
            if (j >= l[i]) g[j] |= g[j - l[i]] | (g[j] << l[i]);
            else g[j] |= g[j] << l[i];
        }
    }
    for (int i = l[n - 1]; d - i >= l[n - 1]; i++) {
        if (g[i][d - i]) return cout << "Yes\n", void();
    }
    cout << "No\n";
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T; while (T--)
        sol();
}