最大m子段和

 

最大m子段和

定义一串子段s1,s2,s3 ... sn-1,sn

求m段不交叉最大子段和

解：
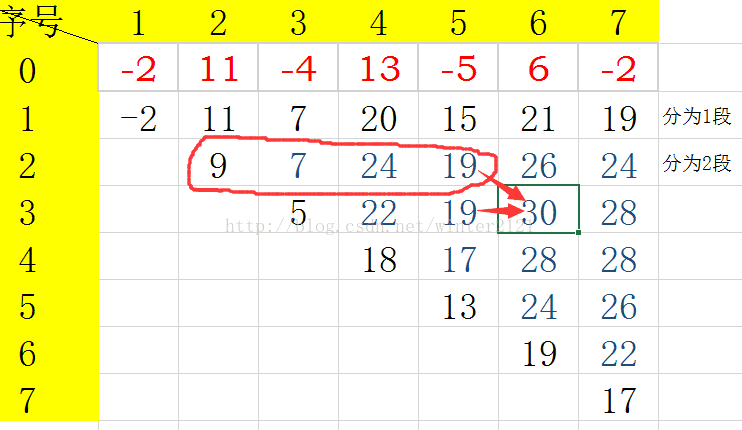
设dp[i][j]代表前j个数分成i段的最大和（包括a[j]）

状态转移方程：

dp[i][j]=Max(dp[i][j-1]+a[j],dp[i-1][t]+a[j]) (i-1=<t<j)

解释两种状态的最优解：
①.a[j]恰好在下一次最优解末项之后，将a[j]融入a[j-1]的子段中，总段数i不变，+a[j]
②.a[j]不在最优解末项之后，而是单独成一段，那么下一次递归对象总段数-1（i-1），末项为
k,i-1=<t<j，k如果小于i-1负溢出。+a[j]

 

 

 

#include<cstdio>
using namespace std;
int main()
{
    int n, num, cnt, ans;
    while(scanf("%d", &n)!=EOF)
    {
        cnt = 0;
        for(int i=0; i<n; i++)
        {
            scanf("%d", &num);
            if(cnt==0)
            {
                ans = num;
                cnt++;
            }
            else
            {
                if(num==ans)
                    cnt++;
                else
                    cnt--;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}