《孙子算经》之"物不知数"题：中国剩余定理

1、《孙子算经》之"物不知数"题

    今有物不知其数，三三数之剩二，五五数之剩七，七七数之剩二，问物几何？

 

2、中国剩余定理

定义：

    设 a,b,m 都是整数.  如果 m|(a-b),  则称 a 和 b 模 m 同余, 记为

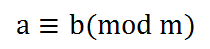
    m 称为这个同余式的模.

定理(中国剩余定理):

    设 m₁,m₂,...,m_r 是两两互素的正整数. 设 a₁,a₂,...,a_r 是整数, 则同余方程组

    模 M = m₁m₂...m_r 有唯一解

 

3、C语言源代码

#include<stdio.h>

//////////////////////////////////////////
// 作者：落枫飘飘
// 时间：2016、04、21
// 博客：http://www.cnblogs.com/wuqianling/p/5415758.html 
//////////////////////////////////////////
// 《孙子算经》之"物不知数"题：
// 今有物不知其数，三三数之剩二，五五数之剩七，七七数之剩二，问物几何？ 
//////////////////////////////////////////
// 根据题意我们有如下同余方程组:
// x=2%3   ---> x=3*k+2
// x=3%5
// x=2%7
//////////////////////////////////////////


// 分析法求解 
int analytical(float m1, float m2, float m3, float a1, float a2, float a3)
{
    float x=0.0, k1=0.0, k2=0.0, k3=0.0;
    
    for(k1 = 0; ; k1++)
    { 
        x = m1*k1 + a1;       // ---> x=3*k1+2
        k2 = (x-a2) / m2;     // ---> k2=(x-2)/3
        if(k2 == (int)k2)     // 判断k2是否为整数 
        {
            k3 = (x-a3) / m3;
            if(k3 == (int)k3) // 判断k3是否为整数
                break; 
        }
    }
    return (int)x;
}


// 中国剩余定理求解 
int chineseRemainderTheorem(int m1, int m2, int m3, int a1, int a2, int a3)
{
    int i, x; 
    int M, M1, M2, M3;
    int y1, y2, y3;
    
    M  = m1 * m2 * m3;
    M1 = m2 * m3;   // M1=M/m1=m2*m3
    M2 = m1 * m3;
    M3 = m1 * m2;
    y1 = M1 % m1;
    y2 = M2 % m2;
    y3 = M3 % m3;
    x  = (a1*M1*y1 + a2*M2*y2 + a3*M3*y3) % M;
    
    return x;
}


int main()
{
    // x=2%3  即 x=a1%m1
    // x=3%5  即 x=a2%m2
    // x=2%7  即 x=a3%m3
    int m1=3, m2=5, m3=7;
    int a1=2, a2=3, a3=2;
    printf("分析法:\nx=%d \n\n", analytical(m1,m2,m3,a1,a2,a3)); 
    printf("中国剩余定理:\nx=%d \n\n", chineseRemainderTheorem(m1,m2,m3,a1,a2,a3));
    return 0;
}