搜索算法初步总结
搜索算法总结
BFS
广度优先搜索一层一层地进行遍历,每层遍历都以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
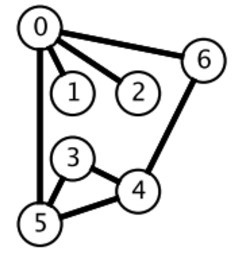
第一层:
- 0 ->
第二层:
- 6 ->
- 2 -> {}
- 1 -> {}
- 5 ->
第三层:
- 4 -> {}
- 3 -> {}
每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离,推导出一个结论:对于先遍历的节点 i 与后遍历的节点 j,有 di <= dj。利用这个结论,可以求解最短路径等 最优解 问题:第一次遍历到目的节点,其所经过的路径为最短路径。应该注意的是,使用 BFS 只能求解无权图的最短路径,无权图是指从一个节点到另一个节点的代价都记为 1。
在程序实现 BFS 时需要考虑以下问题:
- 队列:用来存储每一轮遍历得到的节点;
- 标记:对于遍历过的节点,应该将它标记,防止重复遍历。
BFS模板
之前一直没有总结BFS的模板,就在这简单记录一下,可以加快做题速度
创建队列;
创建访问情况记录数组(数据结构);
while(队列不为空){
poll一个元素;
标记已访问;//已访问情况标记位置比较灵活,也可以在邻域搜索遍历时标记,可以具体问题具体分析
邻域搜索{
if(不合法||已访问)
continue;
if(找到最优解)
返回
入队;
}
}
也可以选择在while循环中再写一个while循环,根据queue.size一次最外层循环遍历一层的元素
创建队列;
创建访问情况记录数组(数据结构);
while(队列不为空){
layer计算当前层数
记录当前queue.size,即当前层元素个数
while (!queue.isEmpty()){
邻域搜索{
if(不合法||已访问)
continue;
if(找到最优解)
返回
入队;
置已访问//个人更习惯在这置已访问
}
}
}
实例如下
public int numSquares_improved(int n) {
int layer = 0;
Queue<Integer> queue = new LinkedList<>();//创建队列
boolean[] visited = new boolean[n + 1];//标记访问情况数组
queue.add(n);
while (!queue.isEmpty()){
layer++;//记录层数
int len = queue.size();//当前层元素个数
for(int i = 0;i < len;i++){//邻域搜索
int current = queue.poll();
for(int j = 1;j * j <= current;j++){
int temp = current - j * j;
if(temp == 0)//找到最优解
return layer;
if(visited[temp])//访问情况以及合法性判断
continue;
queue.add(temp);//入队
visited[temp] = true;//标记已访问
}
}
}
return n;
}
DFS
从一个节点出发,使用 DFS 对一个图进行遍历时,能够遍历到的节点都是从初始节点可达的,DFS 常用来求解这种可达性 问题。
在程序实现 DFS 时需要考虑以下问题:
栈:用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
标记:和 BFS 一样同样需要对已经遍历过的节点进行标记。
DFS模板
回溯法
Backtracking(回溯)属于 DFS。
Backtracking 主要用于求解 排列组合 问题,例如有 { 'a','b','c' } 三个字符,求解所有由这三个字符排列得到的字符串,这种问题在执行到特定的位置返回之后还会继续执行求解过程。
因此在完成程序时需要通过标记操作来完成回溯操作。
在访问一个新元素进入新的递归调用时,将新元素标记为已经访问,这样在继续递归调用时不用重复访问该元素;
但是在递归返回时,需要将元素标记为未访问,因为只需要保证在一个递归链中不同时访问一个元素,可以访问已经访问过但是不在当前递归链中的元素。这就是完成回溯的关键操作。回溯法模板
总结
| 方法 | 适用问题 |
|---|---|
| DFS | 可达性 |
| 回溯法 | 排列组合问题 |
| BFS | 最优解 |


