现实中“二向箔” -----透视投影变换及其投影矩阵
有没有想过这样的问题,计算机是如何把3维的模型显示到2维的屏幕上?照相机又是如何把3维的世界记录成2维的照片的?
发现了吗?世界被降维了!而投影矩阵( Projection Matrix )就是进行这步降维的关键,它就像是一张二向箔,将3维的世界变成一幅幅壮丽的二维画卷.......
有多种类型的投影,比如说正交投影(Orthographic Projection)、透视投影等(Perspective Projection) 。
人的眼睛使用的是透视投影,在这种投影下,同样大小的物体放在近处就会显得比放在远处大。
在这里使用OpenGL里对透视投影矩阵的定义来介绍。
透视投影矩阵要解决一个问题:一个三维坐标上的点,它在一个二维平面(像平面)上的坐标是多少?
相机是小孔成像模型,所有被采集到的光线都要通过光心这一点,于是光心(红点)和原始三维点(蓝点)的连线所交于像平面(蓝线)的点(黄点)就是最终要成像的点。像平面距离光心的距离为n。如下图,假设相机是朝Z轴的负方向看的,并且Z轴穿过光心和像平面的中心。

哎,有读者嫌弃我画的图太丑,其实我也是这么觉得的,没那么多时间画图(好像有时间就能画好似的....)。下面就用参考资料里的图吧。
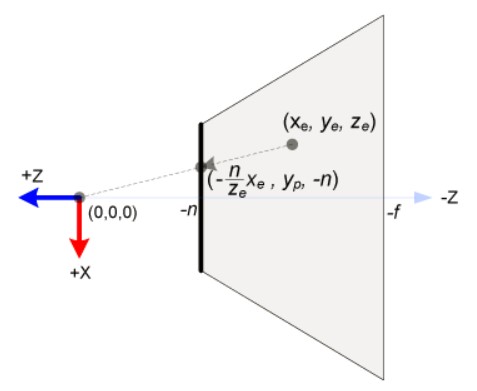
细心的读者会发现图中多个一个平面,距离光心得距离是f,这个平面的意义在于z的值小于-f的点都不会投射到像平面上。至于为什么要多这个far平面嘛.....大家看到最后就会明白了。<( ̄︶ ̄)>
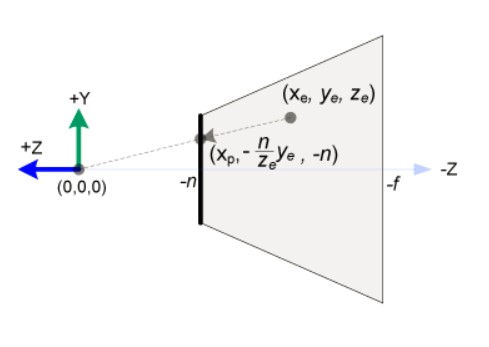
好了,如图所示,根据相似三角形原理,就可以求出一个三维点(xe,ye,ze)在像平面上的坐标(xp,yp)。
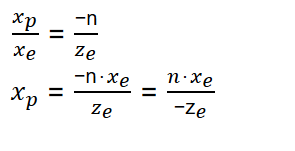
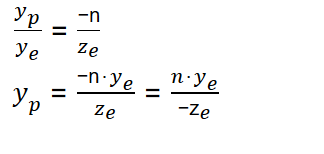
另外,根据opengl的实现,需要将坐标转化成 NDC(normalized device coordinates) ,简单来说,就是定义一定范围的坐标范围,这个范围形成一个类似锥型的区域(frustum),将这个区域内的坐标按照3个坐标轴的方向映射成[-1,1]的值,最终形成一个立方体。
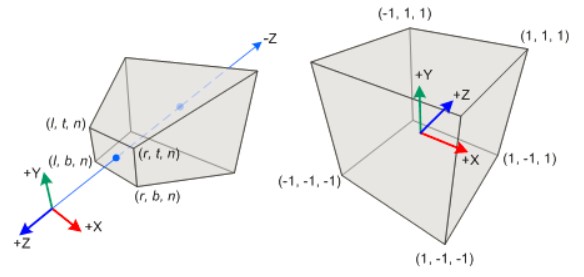
如图所示,例如z=-n的平面被映射成z=-1,z=-f的平面被映射成z=1。
原先的x坐标从[l,r] 被映射成x坐标为[-1,1]
原先的y坐标从[b,t] 被映射成y坐标为[-1,1]。
现在我们需要把这些坐标的变化写成矩阵的形式,写成矩阵 Mprojection。
但是像平面上的坐标(xp,yp)的计算公式中是有除法的,这样的话就没办法写成线性的矩阵运算的形式了。没关系,我们可以使用3维点的齐次坐标(Homogeneous Coordinates) 来运算。
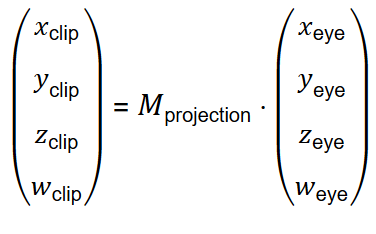
最终就可以获得NDC坐标(发现没?除法出现了!):
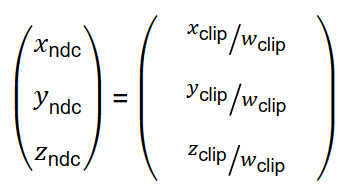
需要构造出Mprojection
因为最后需要除的数是-Ze, 所以需要保证Wclip的值为-Ze, 于是 M矩阵的最后一行应该为[0 0 -1 0].。
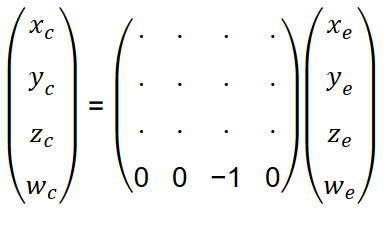
其次,要保证除x和y要被线性映射成[-1,1]。

先设计一个线性方程:
当xp = r 时 xn=1
求解出

又:
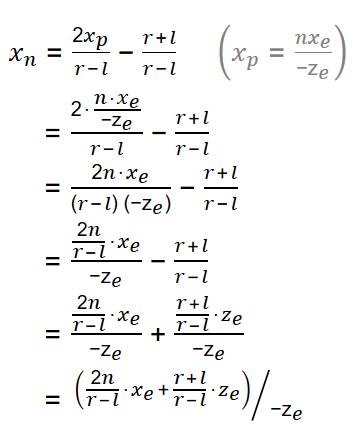
看上是不是就可以写成矩阵形式了?
同理可以获得y方向上的坐标转换公式,就得到了前两行矩阵:

接下来就只剩下第三行需要求解了。
我们知道z的值是不依赖x和y的,于是第三行的前两个元素为0,设另外两个值为A、B:

最终得到的坐标为:
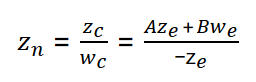
齐次坐标下的w是等于1的,所以等式变为:
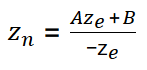
要求解A、B怎么办?找两个点代入进去呀。
这两个点为(-n, -1) 和 (-f, 1)。于是:

解得
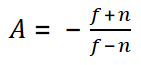
最终,得到了完整的投影矩阵:

注意到没!Ze和Zn的关系不是线性的!
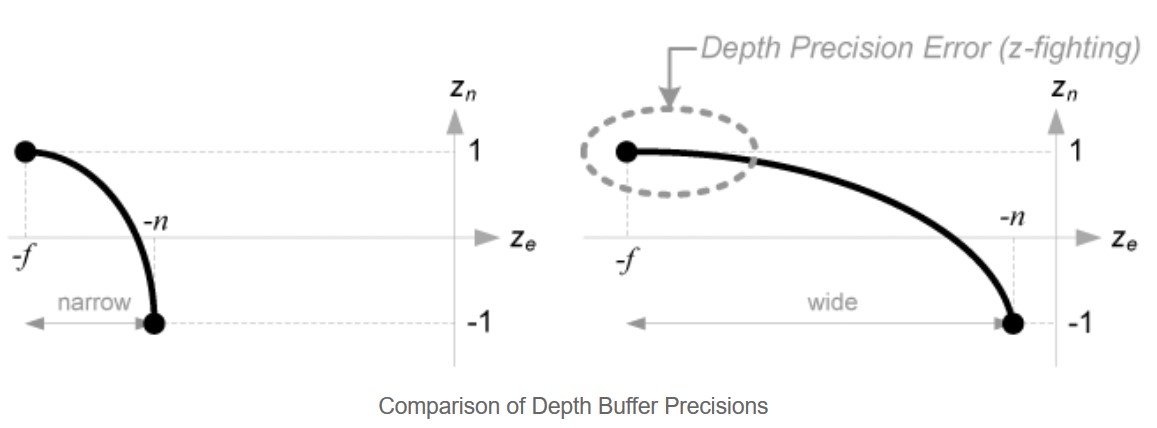
在接近near平面时精度高,在接近far平面时精度低,如果far和near相距较大时,就会产生深度精度问题(z-fighting),所以在满足需求的情况下,far和near要尽可能接近。
好了,世界就这样被二维化了,Enjoy it!
参考资料
http://www.songho.ca/opengl/gl_projectionmatrix_mathml.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号