二维计算几何系列（一） -------- 数据结构

     在二维平面中，只有点和线，点用两个浮点数数表示，而一条线由两个点确定。

const double EPS = 1e-8;    //设置精度
const double PI = acos(-1.0);  //圆周率
int sgn(double x)  //判断负数
{
  if(fabs(x) < EPS)return 0;
  if(x < 0)return -1;
  else return 1;
}
struct Point    //点的数据结构
{
  double x,y;
  Point() {}
  Point(double _x,double _y):x(_x),y(_y){};
  Point operator -(const Point &b)const; //合成向量
  ///叉积
  double operator ^(const Point &b)const;
  ///点积
  double operator *(const Point &b)const;
  ///绕原点旋转角度B（弧度值）产生的新点
  Point transXY(double B) const;
};
struct Line   //线的数据结构，包括直线和线段
{
  Point s,e;
  Line() {}
  Line(Point _s,Point _e):s(_s),e(_e){};
  ///两直线相交求交点
  ///第一个值为0表示直线重合，为1表示平行，为2是相交
  ///只有第一个值为2时，交点才有意义
  pair<int,Point> operator &(const Line &b)const ;
};

struct Point 
 
    该结构不仅可以表示一个点，还可以表示一个以原点为起点的向量。

Point Point::operator -(const Point &b)const
{
     return Point(x - b.x,y - b.y);
}

       减法操作重载，用于向量合成，对应向量的减法。

       

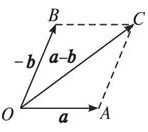
double Point::operator ^(const Point &b)const
{
   return x*b.y - y*b.x;
}

      用于向量叉乘。

      

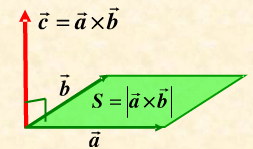
     当a_z=b_z=0时（在二维平面），axb=a_xb_y-a_yb_x=|a||b|sin(a,b);  同时这也是a,b向量围成的平行四边形面积。由于在二维中，所以只有数字没有方向。

double Point::operator *(const Point &b)const
{
    return x*b.x + y*b.y;
}

      获得两向量的数量积。

     

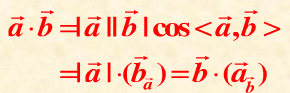
Point Point::transXY(double B) const //绕原点旋转角度B（弧度值）产生的新点
{
    Point ret;
    ret.x = x*cos(B) - y*sin(B);
    ret.y = x*sin(B) + y*cos(B);
    return ret;
}

struct Line 

            两点成线，该结构可以表示直线和线段，至于具体表示的是什么，由使用的算法决定。

 

///两直线相交求交点
///第一个值为0表示直线重合，为1表示平行，为2是相交
///只有第一个值为2时，交点才有意义
pair<int,Point> Line::operator &(const Line &b)const
{
    Point res = s;
    if(sgn((s-e)^(b.s-b.e)) == 0) //直线方向向量的叉积，如果为零，说明两向量平行
    {
      if(sgn((s-b.e)^(b.s-b.e)) == 0)
        return make_pair(0,res);///重合
      else return make_pair(1,res);///平行
    }
    double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
    res.x += (e.x-s.x)*t;
    res.y += (e.y-s.y)*t;
    return make_pair(2,res);
}

       先检测两直线方向向量的叉积，如果为零，说明两向量平行，则对应的直线平行或重合，再构造向量叉乘判断。

       不平行重合的直线只有一个交点，至于如何求交点坐标，这里使用了向量方法，大致的原理是设交点D(x,y),使D在每条直线上的两点构成的向量平行(叉乘为0)，这样两条直线两条方程，求解两个未知数。