左偏树
我们最常用的二叉堆,是最常用的优先队列,它可以在O(logN)内实现插入和删除最小值操作。但是对于合并两个有序的优先队列,二叉堆就显得力不从心了。
左偏树是一种可并堆(Mergeable Heap), 意思是可以在O(logN)时间内完成两个堆的合并操作。左偏树(Leftist Tree),或者叫左倾树,左式树,左式堆(Leftist Heap),左堆。顾名思义,它好象是向左偏的,实际上它是一种趋于非常不平衡的二叉树结构,但却能够实现对数级的合并时间复杂度。
【左偏树的定义】
左偏树(Leftist Tree)是一种可并堆的实现。左偏树是一棵二叉树,它的节点除了和二叉树的节点一样具有左右子树指针( left, right)外,还有两个属性:键值和距离(dist)。键值上面已经说过,是用于比较节点的大小。距离则是如下定义的:
节点i称为外节点(externalnode),当且仅当节点i的左子树或右子树为空( left(i) = NULL或right(i) = NULL );节点i的距离(dist(i))是节点i到它的后代中,最近的外节点所经过的边数。特别的,如果节点i本身是外节点,则它的距离为0;而空节点的距离 规定为-1 (dist(NULL) =-1)。在本文中,有时也提到一棵左偏树的距离,这指的是该树根节点的距离。
【基本性质】
[性质1] 节点的键值小于或等于它的左右子节点的键值。这条性质又叫堆性质。符合该性质的树是堆有序的(Heap-Ordered)。有了这条,我们可以知道左偏树的根节点是整棵树的最小节点。
[性质2] 节点的左子节点的距离不小于右子节点的距离。即dist(left(i))≥dist(right(i)) 这条性质称为左偏性质。
[性质3] 节点的距离等于它的右子节点的距离加1。因为节点距离的定义是离外节点最少的路径长度,而右节点的距离小,肯定是最优的。
左偏树并不是为了快速访问所有的节点而设计的,它的目的是快速访问最小节点以及在对树 修改后快速的恢复堆性质。
从性质中我们可以看到它并不平衡,由于性质2的缘故,它的结构偏向左侧,不过距离的概念和树的深度并不同,左偏树并不意味着左子树 的节点数或是深度一定大于右子树。
[引理1] 若左偏树的距离为一定值,则节点数最少的左偏树是完全二叉树。
[定理1] 若一棵左偏树的距离为k,则这棵左偏树至少有2^(k+1)-1个节点。
[性质4] 一棵N个节点的左偏树距离最多为[log2(N+1)]-1。设一棵N个节点的左偏树距离为k,由定理1可知,N ≥ 2^(k+1)-1,因此k ≤ [log2(N+1)]-1。
标程
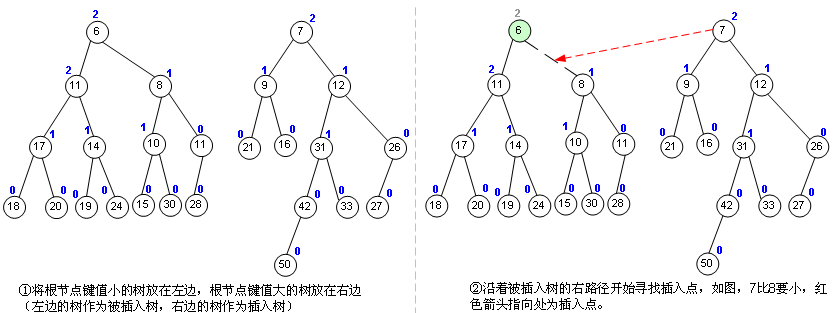
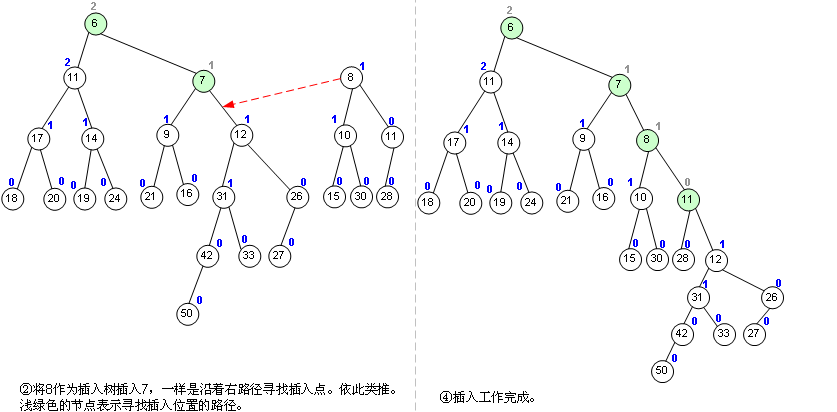
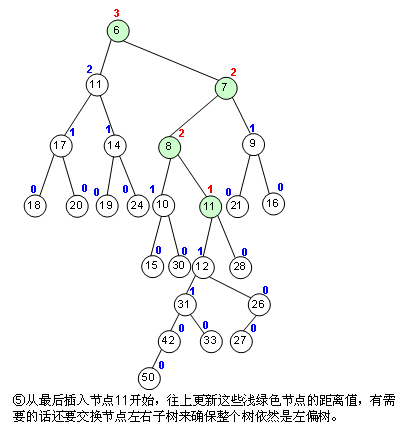
【合并算法】



合并算法用递归的方式更好写出。伪代码:
1 Function Merge(A, B) 2 If A = NULL Then return B 3 If B = NULL Then return A 4 If key(B) < key(A) Then swap(A, B) 5 right(A) ← Merge(right(A), B) 6 If dist(right(A)) > dist(left(A)) Then 7 swap(left(A), right(A)) 8 If right(A) = NULL Then dist(A) ← 0 9 Else dist(A) ← dist(right(A)) + 1 10 return A 11 End Function
合并操作是最重要基本操作。插入操作可以看作是这个左偏树的root和一个单节点树的合并。删除操作可以看作是把root节点取出来,然后合并root的左右子树。
可以证明,一次合并的时间复杂度为O(log2(树A.size) + log2(树B.size))。
[左偏树的构建]
可以用一个队列,使左偏树的构建为O(N)。具体方法为
- 把所有元素作为一个单独左偏树节点放入队列;
- 不断取出两个队首的左偏树,合并这两个左偏树,然后放入队尾;
[对左偏树的比较]
左偏树可以实现二叉堆的一切功能,而且还能实现二叉堆不易实现的合并,个人认为实际编程中左偏树更有理性,不容易错。但左偏树的算法时间常数要大于二叉堆,所以不能完全代替之。
和平衡树相比,左偏树采取了与平衡树完全相反的构造策略。平衡树为了实现所有元素的快速查找,使节点尽量趋于平衡。而左偏树的目的是实现快速的查询最小值与合并操作,恰恰要让节点尽量向左偏。最优的平衡树,恰恰是最差的左偏树,而最优的左偏树,恰恰是平衡树退化的结果。
斜堆、二项堆、斐波那契堆也是可并堆实现的有效方法,而且二项堆、斐波那契堆实际中会比左偏树更快,但是在时间与编程复杂度的性价比上,左偏树有着绝对的优势。
PS:附上我用二叉链表的递归实现
1 struct node 2 { 3 int n,dist; 4 node *left,*right; 5 }; 6 inline void myswap(node *&a,node *&b){node *t=a;a=b;b=t;} 7 inline int getdist(node *a) 8 { 9 if (a==NULL) return -1; //这个情况是要特殊定义值的 10 return a->dist; 11 } 12 node *merge(node *a,node *b) 13 { 14 if (a==NULL) return b; 15 if (b==NULL) return a; 16 if (b->n<a->n) myswap(a,b); 17 a->right=merge(a->right,b); 18 if (getdist(a->right)>getdist(a->left)) myswap(a->left,a->right); 19 a->dist=getdist(a->right)+1;
20 return a; 21 }


