那条矩阵乘法的不归路——数列

话说今天搜矩阵相乘，没有一个人用pascal写，是不是学到矩阵相乘的孩子都果断转c++了。。。我可是有良心的写博人，当然附上pascal代码

故事开始了

今天看到这样一个题

a[1]=a[2]=a[3]=1

a[x]=a[x-3]+a[x-1]  (x>3)

求a数列的第n项对1000000007（10^9+7）取余的值。

然后是它的数据范围

对于30%的数据 n<=100；

对于60%的数据 n<=2*10^7；

对于100%的数据 T<=100，n<=2*10^9；

当我发现打表不过的时候，我就走上了矩阵相乘这条不归路

何谓矩阵相乘

矩阵乘法是一种高效的算法可以把一些一维递推优化到log( n )，还可以求路径方案等，所以更是一种应用性极强的算法。矩阵，是线性代数中的基本概念之一。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起，所以有时候可以简便地表示一些复杂的模型。矩阵乘法看起来很奇怪，但实际上非常有用，应用也十分广泛。——来自好搜百科

 

说白了矩阵相乘就是两个矩阵，其中一个矩阵的长等于另一个矩阵的宽的矩阵相乘，乘出来的新矩阵上f[i,j] 代表第一个矩阵的第i行和第二个矩阵的第j列依次相乘（因为宽等于长，所以可以依次相乘）后累加=>得到新矩阵

 

然后例题来了！

CODEVS  1287 矩阵乘法

题目描述 Description

小明最近在为线性代数而头疼，线性代数确实很抽象（也很无聊），可惜他的老师正在讲这矩阵乘法这一段内容。
当然，小明上课打瞌睡也没问题，但线性代数的习题可是很可怕的。小明希望你来帮他完成这个任务。

现在给你一个ai行aj列的矩阵和一个bi行bj列的矩阵，要你求出他们相乘的积（当然也是矩阵）。
(输入数据保证aj=bi,不需要判断)

矩阵乘法的定义：

1. 矩阵A乘以B的时候，必须要求A的列数=B的行数，否则无法进行乘法运算。因此矩阵乘法也不满足交换律。

2. 设A是X*N的矩阵，B是N*Y的矩阵，用A的每一行乘以B的每一列，得到一个X*Y的矩阵。对于某一行乘以某一列的运算，我们称之为向量运算，即对应位置的每个数字相乘之后求和。

写为公式及：

C[i,j] = Sigma(A[i,k] * B[k,j])

输入描述 Input Description

输入文件共有ai+bi+2行，并且输入的所有数为整数（long long范围内）。
第1行：ai 和 aj
第2~ai+2行：矩阵a的所有元素
第ai+3行：bi 和 bj
第ai+3~ai+bi+3行：矩阵b的所有元素

输出描述 Output Description

输出矩阵a乘矩阵b的积（矩阵c)

样例输入 Sample Input

2 2
12 23
45 56
2 2
78 89
45 56

样例输出 Sample Output

1971 2356
6030 7141

代码其实很简单

注意公式 f[i,j]:=a[i,k]+b[k,j](k是那一条不等边的循环)

program martic;
var a,b:array[1..200,1..200] of int64;
    c:array[1..200,1..200] of int64;
n1,m1,n2,m2,i,j,k:Longint;
begin
    read(n1,m1);
    for i:=1 to n1 do
        for j:=1 to m1 do
        read(a[i,j]);
    read(n2,m2);
    for i:=1 to n2 do
        for j:=1 to m2 do
        read(b[i,j]);
    for i:=1 to n1 do
        for j:=1 to m2 do
            for k:=1 to m1 do
            begin
                c[i,j]:=c[i,j]+a[i,k]*b[k,j];//这是重要的矩阵相乘公式
            end;
    for i:=1 to n1 do
    begin
        for j:=1 to m2 do
        write(c[i,j],' ');
        writeln;
    end;
end.

 

 接下来我就又向那个题迈进了一步，斐波那契数列：

这个题目我主要靠搜的百度，他们要讲的比我讲的明白的多的多，我从各种博客上摘了两种解法（毕竟我百度了一个下午）

给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31

　　根据前面的一些思路，现在我们需要构造一个2 x 2的矩阵，使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵，这两个数就会多迭代一次。那么，我们把这个2 x 2的矩阵自乘n次，再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想，这个2 x 2的矩阵很容易构造出来：

这是一种

另一种 

(三)矩阵乘法+空间换时间(减少乘法，取模运算)

 　　数列的递推公式为：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2)(n>=3)

　　 用矩阵表示为：

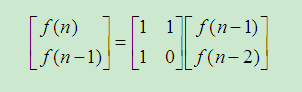
　　进一步，可以得出直接推导公式：

 　　由于矩阵乘法满足结合律，在程序中可以事先给定矩阵的64，32，16，8，4，2，1次方，加快程序的执行时间。（有些题目需要取模运算，也可以事先进行一下）。给定的矩阵次幂，与二进制有关是因为，如下的公式存在解，满足Xi={0或1}： 

 

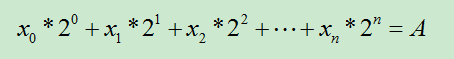
为了保证解满足 Xi={0或1}，对上述公式的求解从右向左，即求解顺序为Xn，Xn-1,Xn-2,....,X1,X0。

我按照的是第一种思路

这里必须说明一点，矩阵里的1就是斜填一条对角线例如（（1,0），（0,1））；

program martic;
type zz=array[1..2,1..2] of int64;
const l:zz=((1,0),
             (0,1));
var a,e:zz;
     n1,n,q,j:Longint;

function mult(m,d:zz; w:longint):zz;
var c:zz;
     i,j,k:longint;
begin
    fillchar(c,sizeof(c),0);
    for i:=1 to 2 do
        for j:=1 to w do
            for k:=1 to 2 do
                 c[i,j]:=(c[i,j]+(m[i,k]*d[k,j])mod q) mod q;
                 exit(c);
end;
function quick(n:longint):Zz;
var m,b,ans:zz;
begin
    m:=a;
    b:=l;
    if n=1 then exit(m);
    while n>=1 do
    begin
        if n mod 2<>0 then b:=mult(b,m,2);
        n:=n div 2;
        m:=mult(m,m,2);
    end;
    exit(b);
end;

begin
    read(n1);
    for j:=1 to n1 do
    begin
        e[1,1]:=1;
        e[2,1]:=1;
        read(n,q);
        a[1,2]:=1;
        a[2,1]:=1;
        a[2,2]:=1;
        a[1,1]:=0;
        a:=quick(n-1);
        e:=mult(a,e,1);
        writeln(e[2,1]);
    end;

end.

后来我就走开时写最上面那个例题

VOJ1067

我们可以用上面的方法二分求出任何一个线性递推式的第n项，其对应矩阵的构造方法为：在右上角的(n-1)*(n-1)的小矩阵中的主对角线上填1，矩阵第n行填对应的系数，其它地方都填0。例如，我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项：

 （越靠近右边的越靠下，我暂时也不知道为什么）

代码如下

program martic;
type zz=array[1..3,1..3] of int64;
const l:zz=((1,0,0),
            (0,1,0),
            (0,0,1));//这就是传说中的初值
      mo=1000000007;
var a,e:zz;
     n1,n,q,j,i:Longint;

function mult(m,d:zz; w:longint):zz;
var c:zz;
     i,j,k:longint;
begin
    fillchar(c,sizeof(c),0);
    for i:=1 to 3 do
        for j:=1 to w do
            for k:=1 to 3 do
                 c[i,j]:=(c[i,j]+(m[i,k]*d[k,j])mod mo) mod mo;
                 exit(c);
end;
function quick(n:longint):Zz;
var m,b,ans:zz;
begin
    m:=a;
    b:=l;
    if n=1 then exit(m);
    while n>=1 do
    begin
        if n mod 2<>0 then b:=mult(b,m,3);
        n:=n div 2;
        m:=mult(m,m,3);
    end;
    exit(b);
end;

begin
    read(n1);
    for j:=1 to n1 do
    begin
        read(n);
        fillchar(a,sizeof(a),0);
        a[1,2]:=1;
        a[2,3]:=1;
        a[3,1]:=1;
        a[3,3]:=1;
        a:=quick(n-3);//因为从第四个值开始，所以要-3
        for i:=1 to 3 do
        e[i,1]:=1;
        e:=mult(a,e,1);
        writeln(e[3,1]);
    end;

end.

至此，我就把我的目标AC掉了，但令人望而生畏的是这个东西有10种例题，我只能在矩阵相乘这条不归路上越走越远。。。。。。