线性svm简单推导及其matlab实现（未完待续）

如图1所示，有a、b两类数据，a类数据有\(a_1, a_2, a_3\)三个样本点，它们的坐标分别为\((a_{1x},a_{1y}),(a_{2x},a_{2y}),(a_{3x},a_{3y})\)，\(a\)类数据的标签为\(t_a=1\), b类数据有\(b_1, b_2, b_3\)三个样本点,它们的坐标分别是\((b_{1x},b_{1y}),(b_{2x},b_{2y}),(b_{3x},b_{3y})\), \(b\)类数据的标签为\(t_b=-1\)。我们的目标是要找出一条直线，\(w_0+w_1x+w_2y=0\)，通过该条直线将\(a,b\)两类数据较好地分离开来，优化目标是使得\(a,b\)两类数据中距离距离该直线最近的样本点到该直线的距离相等且最大，这些样本点也叫做支持向量，例如图1中\(a_1,b_1\)即是支持向量。

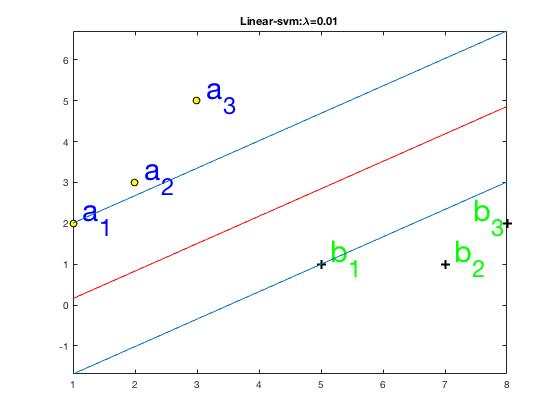
图1 数据分布图

我们使用Hinge loss函数作为cost function。在这里我们将cost function设为：cost=max\((0,1-t * t_p)\), 其中\(t_p\)是预测值, \(t\)是真实值, \(y_p=w_0+w_1* x+w_2*y\)。举例说明，对于点\(a_1\)， 其预测值为\(t_{p_{a1}}=w_0+w_1*a_{1x}+w_2* a_{1y}\), 其cost计算为\(cost_{a1}=max(0,1-t_a* t_{p_a1})\)。

cost function设置为cost=max\((0,1-t* t_p)\)的意义是什么呢？