【机器学习之数学】02 梯度下降法、最速下降法、牛顿法、共轭方向法、拟牛顿法

梯度下降法
- 机器学习中的梯度下降法
最速下降法
- 二次型目标函数
牛顿法
- Levenberg-Marquardt 修正
- 梯度下降法和牛顿法谁快？
共轭方向法
拟牛顿法
- 秩 1 修正公式
References
相关博客

经过前一篇博客的简单介绍，我们对导数、方向导数、梯度应该有一个较为清晰的认识。在知道梯度之后，我们就可以通过一些无约束的优化方法来求极值。

梯度下降法

梯度下降法（Gradient descent），顾名思义，就是自变量沿着梯度向量的反方向进行移动，因为梯度的方向是上升的方向。

对于一个 $R^m \to R$ 的函数 $y = f(\bm x)$，初始时 $\bm x = \bm x^{(0)}$，我们想要得到函数 $y = f(\bm x)$ 的极小值点 $\bm x^*$，如果能够求得 $ f(\bm x)$ 的梯度 $\nabla f(\bm x)$，那么我们就可以用梯度下降法进行迭代求极小值的近似解。(还有不能求梯度的情况吗？还真有，机器学习中如果输入的数据有缺失，那么 loss function 求出的梯度中仍然会含有未知数，这个时候可以用 EM 算法求解)

记自变量 $\bm x$ 在第 $k$ 迭代后的值为 $\bm x^{(k)}$，则自变量的更新公式为：

\[\bm x^{(k+1)} = \bm x^{(k)} - \alpha \cdot \nabla f(\bm x^{(k)}) \tag{1} \]

式（1）中，$\alpha$ 为步长，在深度学习中被称为学习率（learning rate），控制了梯度下降速度的快慢。

机器学习中的梯度下降法

梯度下降法和反向传播算法是深度学习的基石，我们用梯度下降法更新神经网络的参数，用反向传播算法一层一层地将误差由后向前传播（就是用链式法则对 cost function 求偏导）。

如果我们定义 loss function 为

\[L(\bm w) = \bm g(\bm w; (\bm x, y)) = (y - \bm w^{\top} \bm x)^2 \tag{2} \]

那么 cost function 就应该为

\[C(\bm w) = \frac{1}{n}\sum_{i = 1}^n L(\bm w) = \frac{1}{n} \sum_{i = 1}^n (y_i - \bm w^{\top} \bm x_i)^2 \tag{3} \]

其中 $n$ 为一次性计算 loss 的样本个数，在深度学习中常常就是一个 batch 的大小。

cost function/loss function 中，自变量是神经网络的权重，而我们的输入数据是已知的，这个时候我们就可以用用式（4）更新参数了：

\[\bm w^{(k+1)} = \bm w^{(k)} - \alpha \cdot \nabla C(\bm w^{(k)}) \tag{4} \]

如果输入样本 $(\bm x_i, y_i)$ 中含有未知数怎么办？数据缺失了怎么办，在深度学习中，我们可能会选择剔除或者补全数据，然后再输入到神经网络中。如果不补全缺失值，对式（3）算梯度，梯度中会含有未知数，这样式（4）没法更新参数。

假设训练集中含有 $N$ 个数据样本，我们对式（3）中的 $n$ 取不同值（即一次性计算 loss 的样本个数取不同值），会有不同的影响。如果 $n = 1$，这就是 stochastic gradient descent；如果 $1 <n< N$，这就是 mini-batch gradient descent；（mini-batch 的 batch size 一般不会很大。）如果 $n = N$，这就是 (batch) gradient descent。

最速下降法

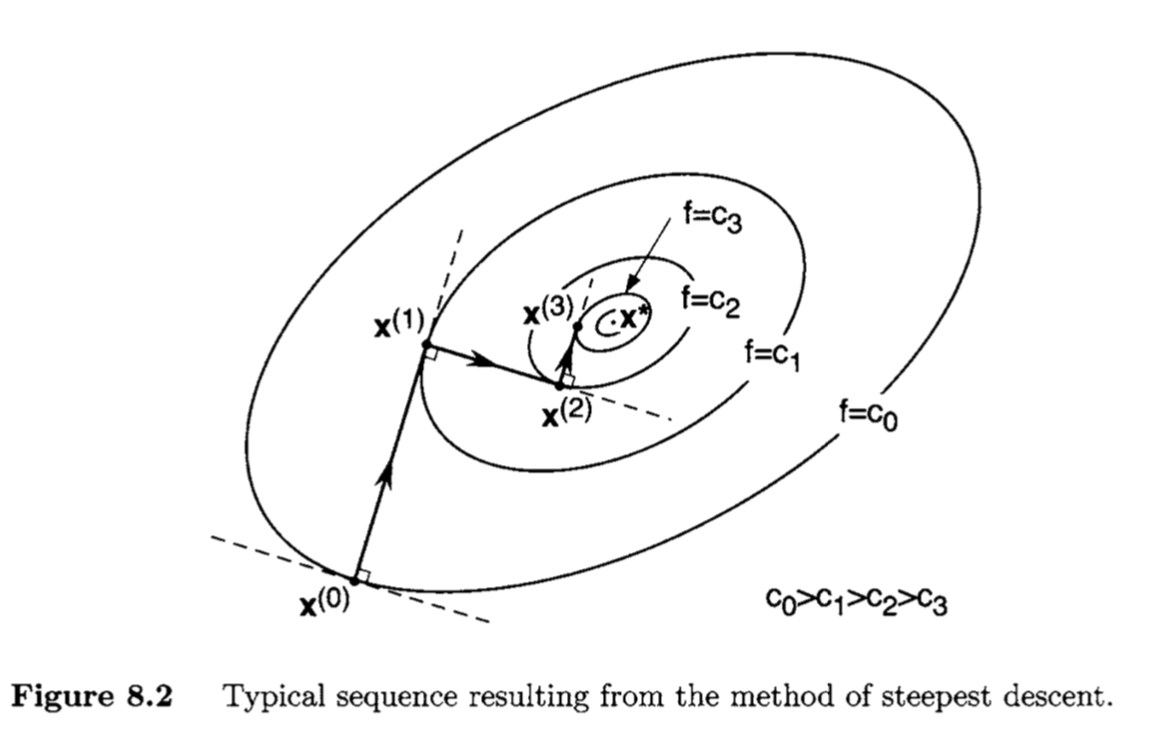
最速下降法（Steepest descent）是梯度下降法的一种更具体实现形式，其理念为在每次迭代中选择合适的步长 $\alpha_k$，使得目标函数值能够得到最大程度的减少。

每一次迭代，沿梯度的反方向，我们总可以找到一个 $\bm x^{(k+1)} = \bm x^{(k)} - \alpha_k \nabla f(\bm x^{(k)})$，使得在这个方向上 $f(\bm x^{(k+1)})$ 取最小值。即

\[\alpha_k = \mathop{\arg\min}_{\alpha \ge 0} f(\bm x^{(k)} - \alpha \nabla f(\bm x^{(k)})) \tag{5} \]

有意思的是，最速下降法每次更新的轨迹都和上一次垂直。而且只要梯度 $\nabla f(\bm x^{(k)}) \not = 0$，则 $f(\bm x^{(k+1)}) < f(\bm x^{(k)})$。（即梯度不等于 0 时，肯定会下降。）具体证明参见《最优化导论》第8.2节。

图 1 steepest descent

二次型目标函数

二次型指的是 $\bm x^{\top} Q \bm x$，$Q$ 是一个对称矩阵，$\bm x$ 是列向量。当 $Q$ 不是对称矩阵时，我们可以做如下变换使其变为对称矩阵：

\[\bm x^{\top} Q \bm x = \bm x^{\top} Q^{\top} \bm x = \bm x^{\top} ( \frac{1}{2}Q + \frac{1}{2}Q^{\top} )\bm x \]

当目标函数为二次型函数时，令目标函数为：

\[f(\bm x) = \frac{1}{2}\bm x^{\top} Q \bm x - \bm b^{\top} \bm x \]

梯度函数为：

\[\nabla f(\bm x) = Q\bm x - \bm b \]

为表示方便，令 $\bm g^{(k)} = \nabla f(\bm x^{(k)})$。

黑塞矩阵为：

\[F(\bm x) = Q = Q^{\top} \]

当目标函数为二次型函数时，我们可以算得每一步的步长取值为：

\[\alpha_k = \frac{\bm g^{(k) \top} \bm g^{(k)}}{\bm g^{(k) \top}Q \bm g^{(k)}} \]

其中，梯度为 $\bm g^{(k)} = \nabla f(\bm x^{(k)}) = Q\bm x^{(k)} - \bm b$。

所以当目标函数为二次型函数时，最速下降法的迭代公式为：

\[\bm x^{(k+1)} = \bm x^{(k)} - \frac{\bm g^{(k) \top} \bm g^{(k)}}{\bm g^{(k) \top}Q \bm g^{(k)}} \bm g^{(k)} \]

牛顿法

在确定搜索方向时，梯度下降和最速下降只用到了目标函数的一阶导数（梯度），而牛顿法（Newton's method）用到了二阶（偏）导数。

Newton's method (sometimes called the Newton-Raphson method) uses first and second derivatives and indeed does perform better than the steepest descent method if the initial point is close to the minimizer.

图 2 Newton's method

牛顿法的基本思路是在每次迭代中，利用二次型函数来局部近似目标函数 $f$，并求解近似函数的极小点作为下一个迭代点，牛顿法自变量 $\bm x$ 的更新公式为：

\[\bm x^{(k+1)} = \bm x^{(k)} - F(\bm x^{(k)})^{-1}\nabla f(\bm x^{(k)}) \]

其中 $F(\bm x^{(k)})^{-1}$ 为二阶偏导数矩阵的逆（即黑塞矩阵的逆）。（为什么更新公式是这样的？可以将 $f(\bm x)$ 在 $\bm x^{(k)}$ 处进行二阶泰勒展开，然后求导。）

Newton's method has superior convergence properties if the starting point is near the solution. However, the method is not guaranteed to converge to the solution if we start far away from it (in fact, it may not even be well-defined because the Hessian may be singular).

当起始点 $\bm x^{(0)}$ 离极值点 $\bm x^*$ 足够近的时候，式（6）的更新公式没有问题。但是，当 $\bm x^{(0)}$ 离极值点 $\bm x^*$ 较远时，我们并不能保证牛顿法能收敛到极值点。甚至，牛顿法可能都不是一个 descent 的方法，即可能 $f(\bm x^{(k+1)}) \ge f(\bm x^{(k)})$。幸运的是可以做一点修改，确保牛顿法是一个 descent 的方法。（黑塞矩阵如果不是正定的，那就要对牛顿法进行修正，如 Levenberg-Marquardt 修正。）

如果黑塞矩阵正定（$F(\bm x^{(k)}) > 0$ ），并且 $\nabla f(\bm x^{(k)}) \not = 0$，那么我们的搜索的方向为

\[\bm d^{(k)} = - F(\bm x^{(k)})^{-1}\nabla f(\bm x^{(k)}) = \bm x^{(k+1)} - \bm x^{(k)} \]

要想从 $\bm x^{(k)}$ 到 $\bm x^{(k+1)}$ 是 descent direction，只要存在一个 $\overline \alpha > 0$，使得所有 $\alpha \in (0, \overline \alpha)$，满足 $f(\bm x^{(k)} + \alpha \bm d^{(k)}) < f(\bm x^{(k)})$。
此时牛顿法的更新公式为：

\[\bm x^{(k+1)} = \bm x^{(k)} - \alpha_kF(\bm x^{(k)})^{-1}\nabla f(\bm x^{(k)}) \]

对于 $\alpha_k$，我们也可以在方向 $\bm d^{(k)}$ 上进行线性搜索，使得 $\alpha_k = \mathop{\arg\min}_{\alpha \ge 0} f(\bm x^{(k)} - \alpha F(\bm x^{(k)})^{-1}\nabla f(\bm x^{(k)}))$。

这个时候，梯度下降法和牛顿法除了一个黑塞矩阵外，是不是超级像了。如果黑塞矩阵不是正定的，那就要对牛顿法进行修正，如 Levenberg-Marquardt 修正。

Levenberg-Marquardt 修正

如果黑塞矩阵 $ F(\bm x^{(k)})$ 不正定，那么搜索方向 $\bm d^{(k)} = - F(\bm x^{(k)})^{-1}\nabla f(\bm x^{(k)})$ 可能不会是下降方向。牛顿法的 Levenberg-Marquardt 修正可以解决这个问题：

\[\bm x^{(k+1)} = \bm x^{(k)} - \alpha_k(F(\bm x^{(k)}) + \mu_k \bm I)^{-1}\nabla f(\bm x^{(k)}) \]

其中，$\mu_k \ge 0$，$\bm I$ 为单位矩阵。在该修正中， $ F(\bm x^{(k)})$ 可以不正定，但是 $\bm G = F(\bm x^{(k)}) + \mu_k \bm I$ 需要是正定的，所以，取适当的 $\mu_k$，使得 $\bm G$ 正定即可。（矩阵正定，当前仅当所有特征值大于 0。）

$\mu_k$ 过大也不行，否则就相当于步长取了很小的值。（逆过小或者是分母过大。）

梯度下降法和牛顿法谁快？

可能会有一个疑问，梯度下降法中梯度的反方向不是当前点下降最快的方向吗，为什么牛顿法会收敛更快，牛顿法的更新方向更好吗？

牛顿法是二阶收敛，梯度下降法是一阶收敛，所以牛顿法就更快。
更通俗地，梯度下降法只从当前位置选择一个坡度最大的方向走一步，而牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑走了一步后，坡度是否会变得更大。
从几何上说，牛顿法就是用一个二次曲面去拟合当前位置的的局部曲面，而梯度下降法用的是一个平面去拟合，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

详情参见最优化问题中，牛顿法为什么比梯度下降法求解需要的迭代次数更少？ -- 大饼土博。

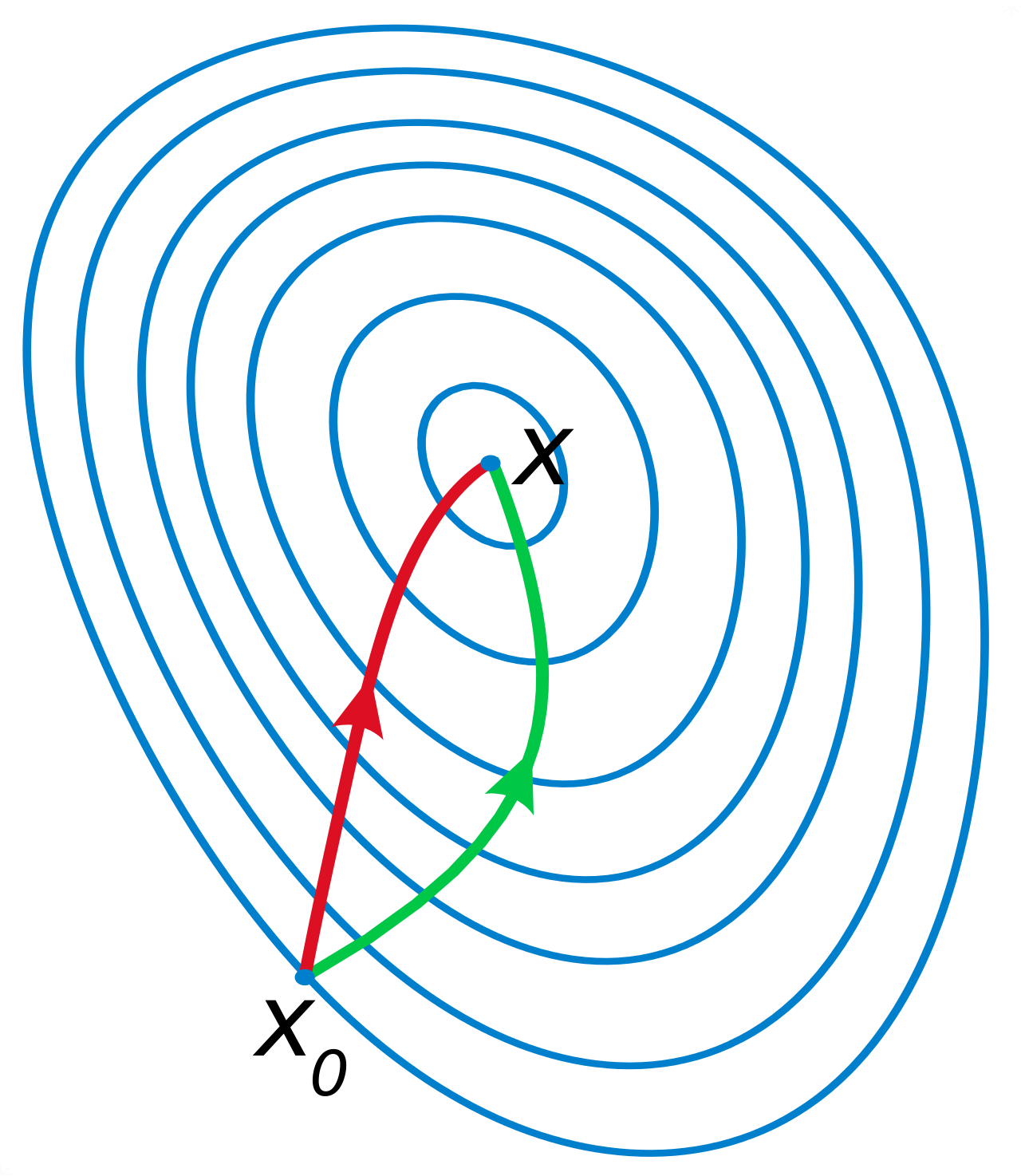
图 3 A comparison of gradient descent (green) and Newton's method (red) for minimizing a function (with small step sizes).
Newton's method uses curvature information (i.e. the second derivative) to take a more direct route.

共轭方向法

共轭方向法的性能优于最速下降法，但不如牛顿法。

共轭方向法具有以下特性：

对于 n 维二次型问题，能够在 n 步之内求得结果；
作为共轭方向法的典型代表，共轭梯度法不需要计算黑塞矩阵；
不需要存储 $n \times n$ 的矩阵，也不需要对其求逆。

考虑一个二次型函数 $f(\bm x) = \frac{1}{2}\bm x^{\top} Q \bm x - \bm b^{\top} \bm x$，其中 $\bm x \in \mathbb{R}^n$，$Q = Q^{\top}>0$。（这里没有考虑非二次型问题中的共轭方向法/共轭梯度法，有需要的直接参考《最优化导论》 10.4 节）

什么是共轭方向？

设 $Q$ 为 $n \times n$ 的正定对称实矩阵，对于方向 $\bm d^{(0)},\bm d^{(1)},\bm d^{(2)},... ,\bm d^{(n-1)}$，如果对于所有的 $i \not = j$，有 $d^{(i) \top} Q d^{(j)} = 0$，则称它们是关于 $Q$ 共轭的，且是线性无关的。

基本的共轭方向法

给定初始点 $\bm x^{(0)}$ 和一组关于 $Q$ 的共轭方向 $\bm d^{(0)},\bm d^{(1)},\bm d^{(2)},... ,\bm d^{(n-1)}$，迭代公式如下：（$k \ge 0$ 表示迭代次数）

\[\bm g^{(k)} = \nabla f(\bm x^{(k)}) = Q\bm x^{(k)} - \bm b \\ \alpha_k = - \frac{\bm g^{(k) \top} \bm d^{(k)}}{\bm d^{(k) \top} Q \bm d^{(k)}} \\ \bm x^{(k+1)} = \bm x^{(k)} + \alpha_k \bm d^{(k)} \]

上式和最速下降法的公式很像，当更新方向为梯度的方向，即 $\bm d^{(k)} = - \bm g^{(k)}$ 时，共轭方向法和最速下降法就长得一模一样了。当然，这一般是不可能的，共轭方向法要求更新方向是共轭的。

上式中 $\alpha_k$ 的更新公式有个负号，但这个数是个正数，将 $\bm d^{(k)} = - \bm g^{(k)}$ 带入就可以知道。

共轭方向法的计算效率很高，但前提是给定一组 $Q$ 共轭方向。共轭梯度法不需要提前给定一组 $Q$ 共轭方向，而是随着迭代的进行，逐一产生 $Q$ 共轭方向。

共轭梯度法

作为共轭方向法的典型代表，共轭梯度法不同之处在于其 $Q$ 共轭方向的获取，每一次迭代，我们需要当场生成下一次迭代的方向：

\[\bm d^{(k+1)} = - \bm g^{(k+1)} + \beta_k \bm d^{(k)}, k = 0,1,2,... \]

按照如下方式选择系数 $\beta_k$，可以使得新生成的方向 $\bm d^{(k+1)}$ 和之前的方向 $\bm d^{(0)}, \bm d^{(1)}, ..., \bm d^{(k)}$ $Q$ 共轭：

\[\beta_k = \frac{\bm g^{(k+1) \top} Q \bm d^{(k)}}{\bm d^{(k) \top} Q \bm d^{(k)}} \]

对于初始方向 $\bm d^{(0)}$，直接用负梯度即可，即 $\bm d^{(0)} = - \bm g^{(0)}$。

拟牛顿法

牛顿法需要计算黑塞矩阵 $F(\bm x^{(k)})$ 并且计算它的逆 $F(\bm x ^ {(k)})^{ -1}$，求逆并不是很简单。

为了避免 $F(\bm x ^ {(k)})^{ -1}$ 这种矩阵求逆运算，可以通过设计 $F(\bm x ^ {(k)})^{ -1}$ 的近似矩阵来代替 $F(\bm x ^ {(k)})^{ -1}$，这就是拟牛顿法的基本思路。

在拟牛顿法中，$F(\bm x ^ {(k)})^{ -1}$ 近似矩阵 $\bm H_k$ 的构建只需要用到目标函数值和梯度。

拟牛顿法的更新公式为：

\[\bm x^{(k+1)} = \bm x^{(k)} - \alpha_k \bm H_k \nabla f(\bm x^{(k)}) \]

拟牛顿法的更新方向 $\bm d^{(k)} = -\bm H_k \nabla f(\bm x^{(k)})$，当目标函数为二次型时，这些方向其实也是关于 $Q$ 共轭的，即拟牛顿法也是一种共轭方向法。

拟牛顿法的关键在于求出 $\bm H_{k+1}$，给出 $\bm H_k$、梯度 $f(\bm x^{(k)})$、$\bm d^{(k)}$、$\alpha_k$，找到 $\bm H_{k+1}$ 的递推式，那么在迭代过程中就不需要涉及到黑塞矩阵也不会求逆。

秩 1 修正公式

$\bm H_{k+1}$ 的递推式为：

\[\boldsymbol{H}_{k+1}=\boldsymbol{H}_{k}+\frac{\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_{k} \Delta \boldsymbol{g}^{(k)}\right)\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_{k} \Delta \boldsymbol{g}^{(k)}\right)^{\top}}{\Delta \boldsymbol{g}^{(k) \top}\left(\Delta \boldsymbol{x}^{(k)}-\boldsymbol{H}_{k} \Delta \boldsymbol{g}^{(k)}\right)} \]

其中，$\Delta x^{(k)}=\alpha_{k} d^{(k)}$，$\Delta \boldsymbol{g}^{(k)}=\boldsymbol{g}^{(k+1)}-\boldsymbol{g}^{(k)}$。

$\bm H_0$ 可以取任一对称正定实矩阵。

References

Edwin K. P. Chong, Stanislaw H. Zak-An Introduction to Optimization, 4th Edition
最优化问题中，牛顿法为什么比梯度下降法求解需要的迭代次数更少？ -- 大饼土博
 Newton's method in optimization - Wikipedia

wuliytTaotao

努力努力再努力(ง •̀_•́)ง 研究方向：计算广告、主动学习、半监督学习