贝叶斯深度学习(bayesian deep learning)
本文简单介绍什么是贝叶斯深度学习(bayesian deep learning),贝叶斯深度学习如何用来预测,贝叶斯深度学习和深度学习有什么区别。对于贝叶斯深度学习如何训练,本文只能大致给个介绍。(不敢误人子弟)
在介绍贝叶斯深度学习之前,先来回顾一下贝叶斯公式。
贝叶斯公式
其中,\(p(z|x)\) 被称为后验概率(posterior),\(p(x, z)\) 被称为联合概率,\(p(x|z)\) 被称为似然(likelihood),\(p(z)\) 被称为先验概率(prior),\(p(x)\) 被称为 evidence。
如果再引入全概率公式 \(p(x) = \int p(x|z)p(z) dz\),式(1)可以再变成如下形式:
如果 \(z\) 是离散型变量,则将式(2)中分母积分符号 \(\int\) 改成求和符号 \(\sum\) 即可。(概率分布中的概率质量函数一般用大写字母 \(P(\cdot)\) 表示,概率密度函数一般用小写字母 \(p(\cdot)\) 表示,这里为了简便,不多做区分,用连续型变量举例)
什么是贝叶斯深度学习?
一个最简单的神经元网络结构如下图所示:
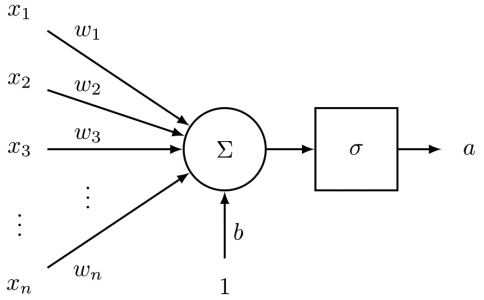
在深度学习中,\(w_i, (i = 1,...,n)\) 和 \(b\) 都是一个确定的值,例如 \(w_1 = 0.1, b = 0.2\)。即使我们通过梯度下降(gradient decent)更新 \(w_i = w_i - \alpha\cdot\frac{\partial J}{\partial w_i}\),我们仍未改变 “\(w_i\) 和 \(b\) 都是一个确定的值” 这一事实。
那什么是贝叶斯深度学习?将 \(w_i\) 和 \(b\) 由确定的值变成分布(distributions),这就是贝叶斯深度学习。
贝叶斯深度学习认为每一个权重(weight)和偏置(bias)都应该是一个分布,而不是一个确定的值。(这很贝叶斯。)如下图所示,给出一个直观的例子:
图 2 展示了一个结构为 4x3x1 的贝叶斯神经网络。(输入层神经元个数为 4,中间隐含层神经元个数为 3,输出层神经元个数为 1。)
贝叶斯深度学习如何进行预测?
说了这么多,贝叶斯神经网络该怎么用?网络的权重和偏置都是分布,分布咋用,采样呗。想要像非贝叶斯神经网络那样进行前向传播(feed-forward),我们可以对贝叶斯神经网络的权重和偏置进行采样,得到一组参数,然后像非贝叶斯神经网络那样用即可。
当然,我们可以对权重和偏置的分布进行多次采样,得到多个参数组合,参数的细微改变对模型结果的影响在这里就可以体现出来。这也是贝叶斯深度学习的优势之一,多次采样最后一起得到的结果更加 robust。
贝叶斯深度学习如何进行训练?
对于非贝叶斯神经网络,在各种超参数固定的情况下,我们训练一个神经网络想要的就是各个层之间的权重和偏置。对于贝叶斯深度学习,我们训练的目的就是得到权重和偏置的分布。这个时候就要用到贝叶斯公式了。
给定一个训练集 \(D= \{( \bm{x}_1, y_1), (\bm{x}_2, y_2),..., (\bm{x}_m, y_m)\}\),我们用 \(D\) 训练一个贝叶斯神经网络,则贝叶斯公式可以写为如下形式:
式(3)中,我们想要得到的是 \(w\) 的后验概率 $p(w|\bm{x}, y) $,先验概率 \(p(w)\) 是我们可以根据经验也好瞎猜也好是知道的,例如初始时将 \(p(w)\) 设成标准正态分布,似然 \(p(y|\bm{x}, w)\) 是一个关于 \(w\) 的函数。当 \(w\) 等于某个值时,式(3)的分子很容易就能算出来,但我们想要得到后验概率 \(p(w|\bm{x}, y)\),按理还要将分母算出来。但事实是,分母这个积分要对 \(w\) 的取值空间上进行,我们知道神经网络的单个权重的取值空间可以是实数集 \(R\),而这些权重一起构成的空间将相当复杂,基本没法积分。所以问题就出现在分母上。
贝叶斯深度学习的训练方法目前有以下几种:(请参考Deep Bayesian Neural Networks. -- Stefano Cosentino)
(1)Approximating the integral with MCMC
(2)Using black-box variational inference (with Edward)
(3)Using MC (Monte Carlo) dropout
第(1)种情况最好理解,用 MCMC(Markov Chains Monte Carlo) 采样去近似分母的积分。第(2)种直接用一个简单点的分布 \(q\) 去近似后验概率的分布 \(p\),即不管分母怎么积分,直接最小化分布 \(q\) 和 \(p\) 之间的差异,如可以使用 KL散度 计算。详情可以参考贝叶斯编程框架 Edward 中的介绍。第(3)种,蒙特卡罗 dropout,简单而强大,不改变一般神经网络结构,只是要求神经网络带 dropout 层,训练过程和一般神经网络一致,只是测试的时候也打开 dropout,并且测试时需要多次对同一输入进行前向传播,然后可以计算平均和统计方差。
贝叶斯深度学习和深度学习有什么区别?
通过之前的介绍,我们也可以发现,在深度学习的基础上把权重和偏置变为 distribution 就是贝叶斯深度学习。
贝叶斯深度学习还有以下优点:
(1)贝叶斯深度学习比非贝叶斯深度学习更加 robust。因为我们可以采样一次又一次,细微改变权重对深度学习造成的影响在贝叶斯深度学习中可以得到解决。
(2)贝叶斯深度学习可以提供不确定性(uncertainty),非 softmax 生成的概率。详情参见 Deep Learning Is Not Good Enough, We Need Bayesian Deep Learning for Safe AI。
贝叶斯神经网络(Bayesian neural network)和贝叶斯网络(Bayesian network)?
请不要混淆贝叶斯神经网络和贝叶斯网络这两者的概念。
“贝叶斯网络(Bayesian network),又称信念网络(belief network)或是有向无环图模型(directed acyclic graphical model),是一种概率图型模型。”
而贝叶斯神经网络(Bayesian neural network)是贝叶斯和神经网络的结合,贝叶斯神经网络和贝叶斯深度学习这两个概念可以混着用。
贝叶斯深度学习框架
References
Eric J. Ma - An Attempt At Demystifying Bayesian Deep Learning
Deep Bayesian Neural Networks. -- Stefano Cosentino
Edward -- A library for probabilistic modeling, inference, and criticism.
Deep Learning Is Not Good Enough, We Need Bayesian Deep Learning for Safe AI
贝叶斯网络 -- 百度百科


 浙公网安备 33010602011771号
浙公网安备 33010602011771号