一个 很好的题目；

转载过来的

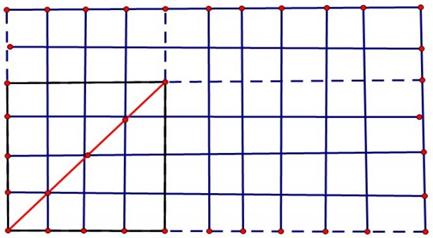
  Zoj 3647 Gao the Grid  ssslpk AC的题。在一个n*m个方格中（顶点有（n+1）*(m+1)个），求所有三角形数，即三点不共线的所有情况。令所有点的个数为t,用c[t,3]来枚举所有情况，用总数扣去所有三点共线数就是所求的三角形数。那么在求三点共线的情况时，水平和垂直的情况读者自己考虑。对于倾斜的情况，先枚举两端的端点，如图，在一个6*10的方格中选4*4的两个端点，其中可构成三点花线的另一点的个数为最大公约数gcd(4,4) -1.如图中的三个点，然后用乘于剩下的倍数（6-4+1）*（10-4+1），再乘于2（倾斜时有右上，右下两种情况）.然后依次枚举所有的矩形，求出所有三点共线的情况。于是所有情况减三点共线情况就是答案了。

    

对于整x,y
x/y=w/h
x*h=y*w
y=x*h/w
这儿可以化简一下
h=h1*d
w=w1*d
d=gcd(h,w)
y=x*h1/w1
那么x必须是w1 的倍数了。
而且y<=h
那么x*h1/w1<=h
x<=h/h1*w1=d*w1=w
也就是要求一下x<=w里面有几个 x%w1==0
那么x可以是w1,2*w1,3*w1,4*w1...,(d-1)*w1
d=gcd(w,h)
命题得证。