PSO算法

一、粒子群算法的概述

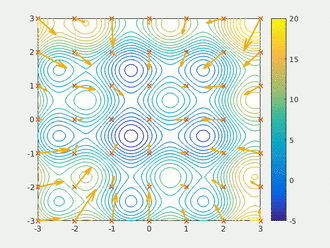
    粒子群算法(PSO)属于群智能算法的一种，是通过模拟鸟群捕食行为设计的。假设区域里就只有一块食物（即通常优化问题中所讲的最优解），鸟群的任务是找到这个食物源。鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群，最终，整个鸟群都能聚集在食物源周围，即我们所说的找到了最优解，即问题收敛。

二、粒子群算法分析

1、基本思想

  粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。下面的动图很形象地展示了PSO算法的过程：

 

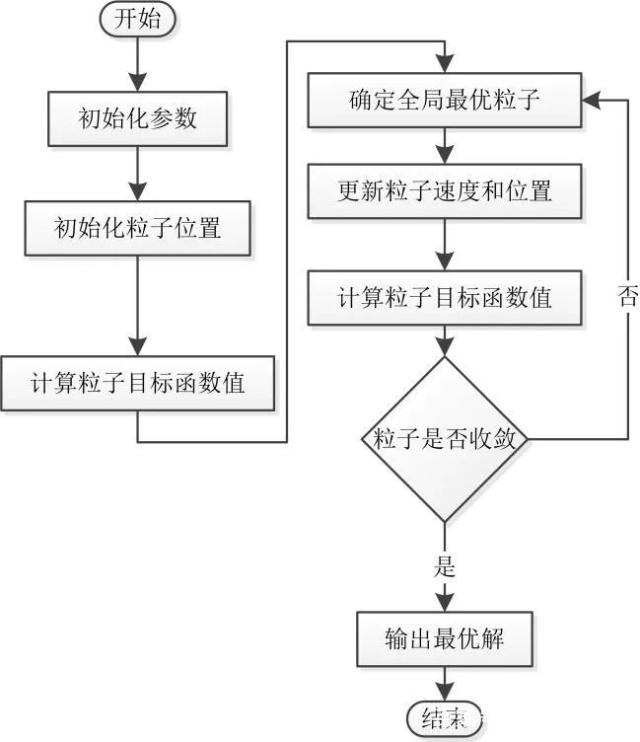
2. 粒子群的算法流程：

 

 3.算法的公式

 三、实验结果及分析

一、c1,c2,w对实验的影响

1.1 c1，c2不变，w对实验的影响

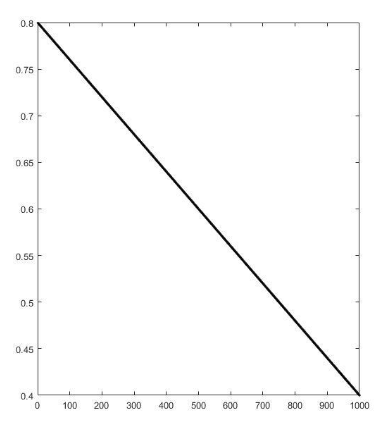
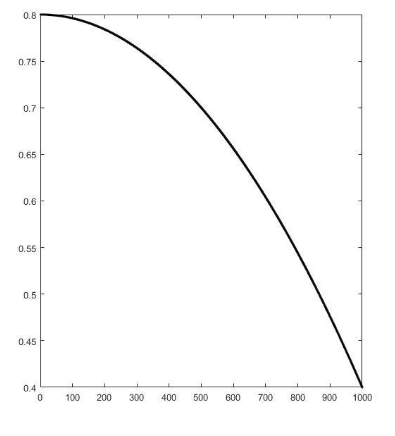
1.典型线性递减策略的w计算公式如下：

w=0.8-(0.4/1000)*i;

w的变化如图所示：

 

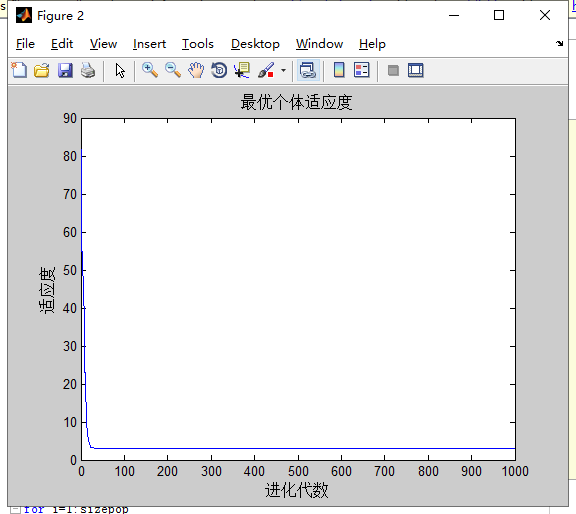
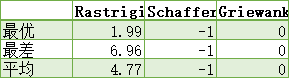
 测试w对三种函数的影响

Rastrigin　　　　　　　　　　　　　　　　　　Schaffer

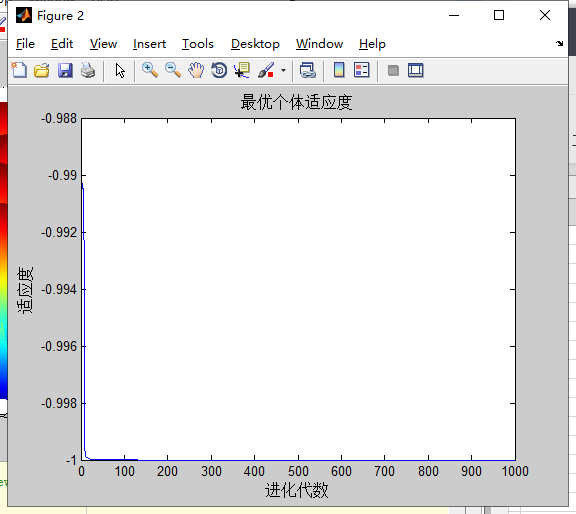
Griewank

 

 

 计算5次的结果

 

 

1.线性微分递减策略的w的计算公式如下：

w=0.8-(0.4/1000000)*i*i;

w的变化如图所示：

 

 

 

 

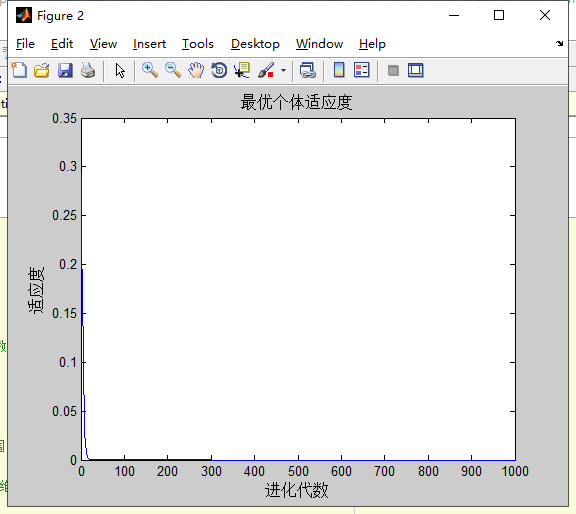
 测试w对三种函数的影响

Rastrigin　　　　　　　　　　　　　　Schaffer

 

 

 

 

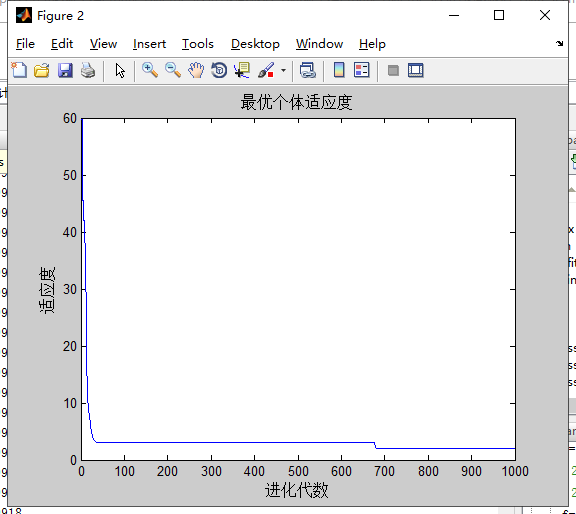
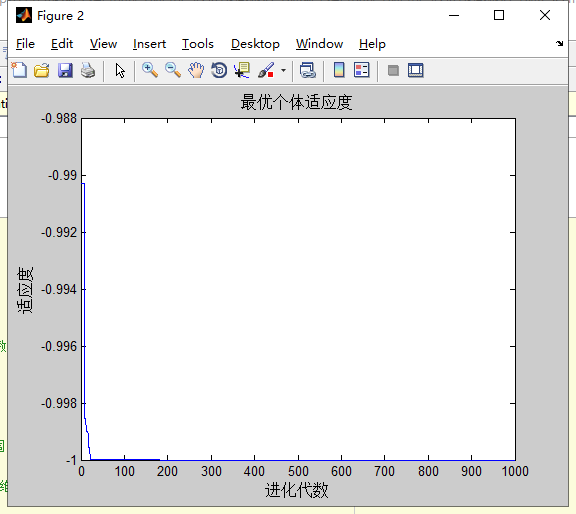
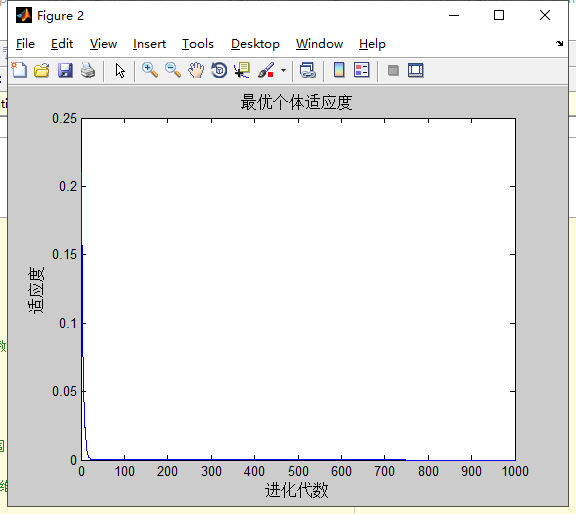
 Griewank

 

 

  计算5次的结果

 

 

 

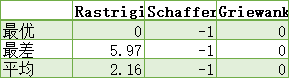
 分析：两种类型的w在面对Griewank多次计算都达到了理论的最优解，而面对Schaffer时多次计算都是-1。在面对Rastrigin时，第二种类型w精度比第一种类型高，且第二种类型w几次达到理论最优解，而且第一种w多次计算均为得到0。第二种类型w收敛速度比第一种类型快。

第一种类型w使得PSO更好的控制全局搜索能力和局部搜索能力，但如果在初期搜索不到最好点，那么随着w的减小，局部搜索能力加强，就容易陷入局部最优中。

第二种类型w在算法初期w减小趋势缓慢，全局搜索能力强，有利于找到很好的优化种子，在算法后期，w减小趋势加快，如果前期找到合适的种子，可以使得算法收敛速度加快。

 1.2 w不变，c1,c2对实验的影响

 

 

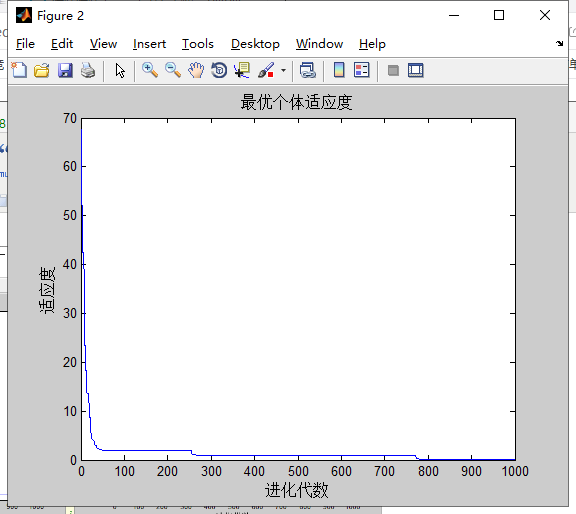
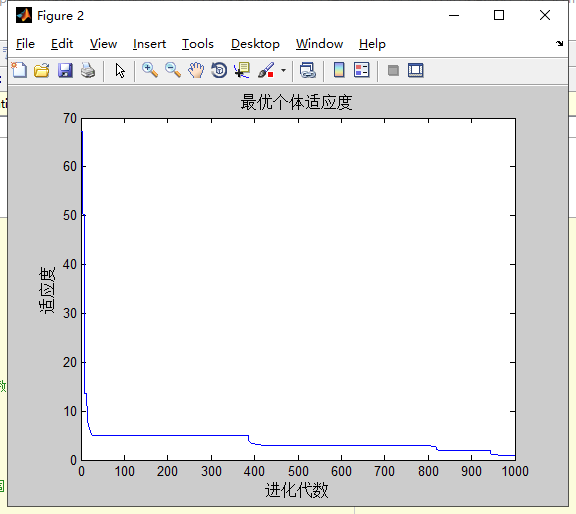
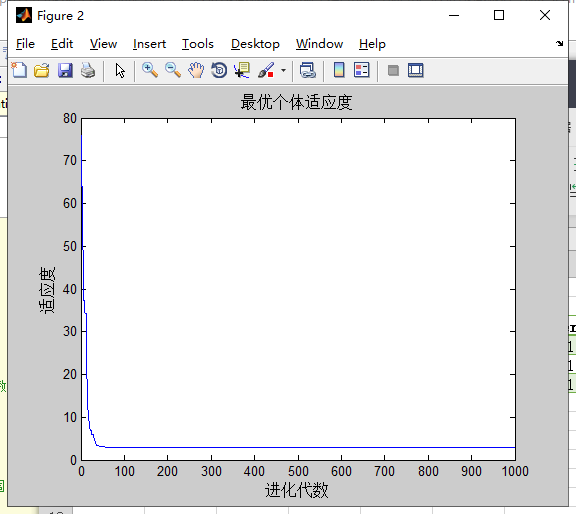
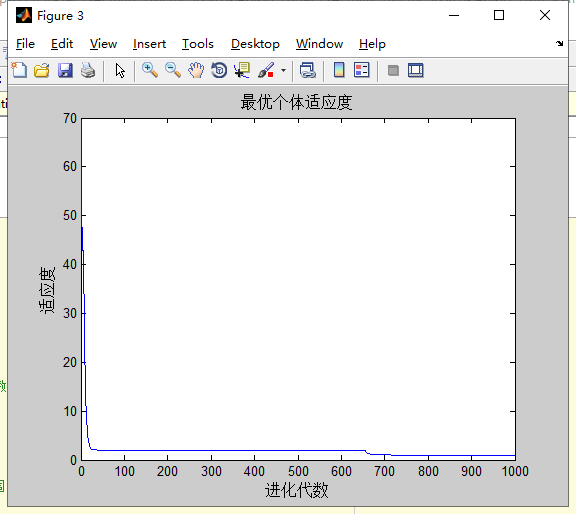
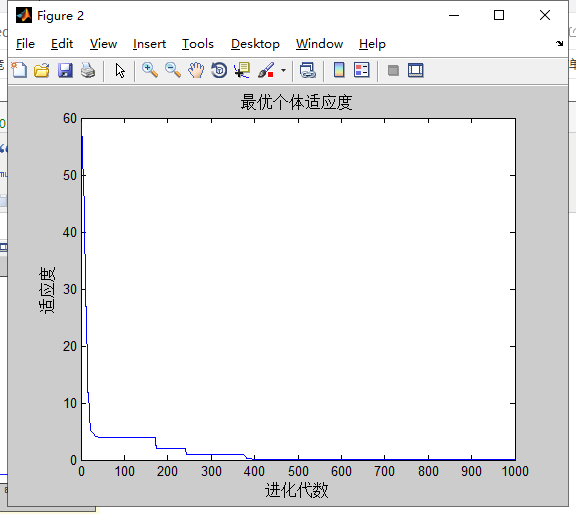
计算的结果：

 

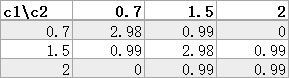
 分析：过大或过小的c1,c2都将使优化过程陷入局部最优解中。

1.c1,c2过小时，自身经验和社会经验在整个寻优过程中所起的作用小，使得寻优过程过于随机。

2.c1,c2过大时，调整的幅度过大，容易陷入局部最优中。

3.c1相对小，c2相对大时，将盲目的向gbest快速聚集，收敛速度加快的同时，盲目性使得粒子容易错过更好解，陷入局部最优中。

4.c1相对大，c2相对小时，粒子寻路线趋于多样化。粒子行为分散，而且进化速度慢，导致收敛速度慢，有时可能难以收敛。

 

 1.3 c1，c2，w对实验的影响

三者都成线性变化

w=(-0.4)/1000*i+0.8;
c1=0.5/1000*i+1.5;
c2=0.5/1000*i+1.5;

Rastrigin　　　　　　　　　　　　Schaffer　　　　　　　　　　Griewank

 

 

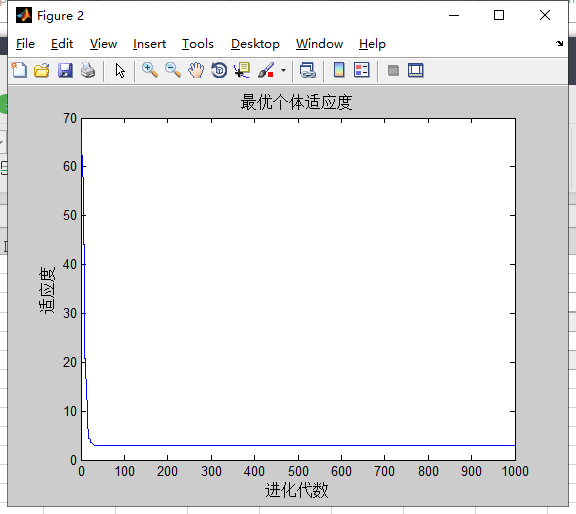
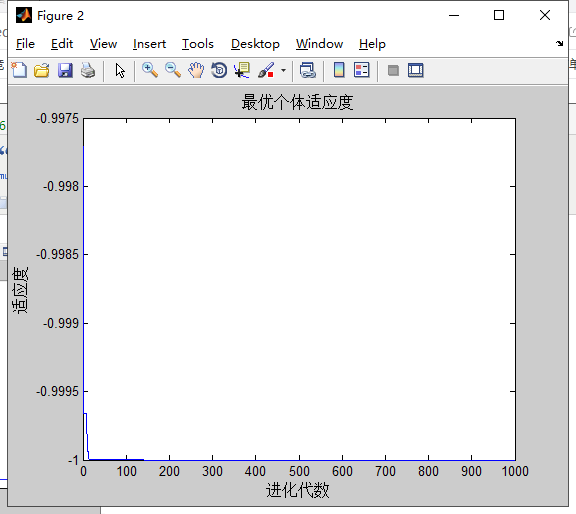
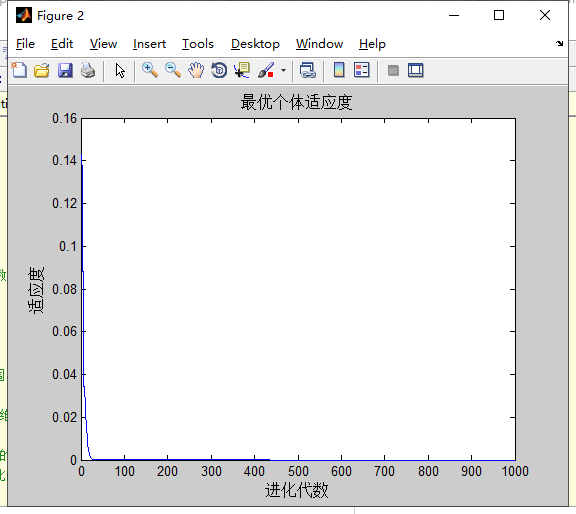
 计算5次的结果

 

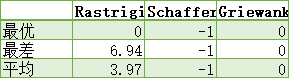
 分析：和之前只有w改变的实验结果差不多，可能三个都改变的影响下，w的改变占主导地位。w的影响最大。

 

 二、sizepop和dim对实验的影响

 

 

 

 

 

 

 

 

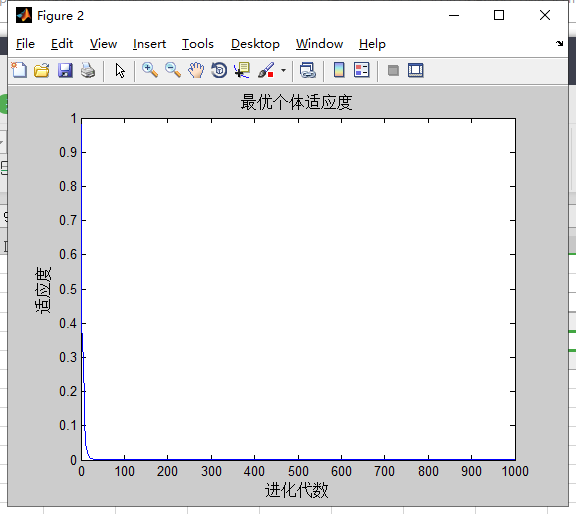
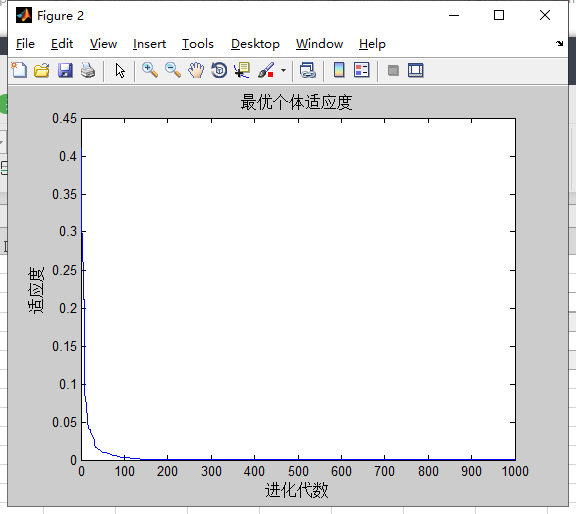
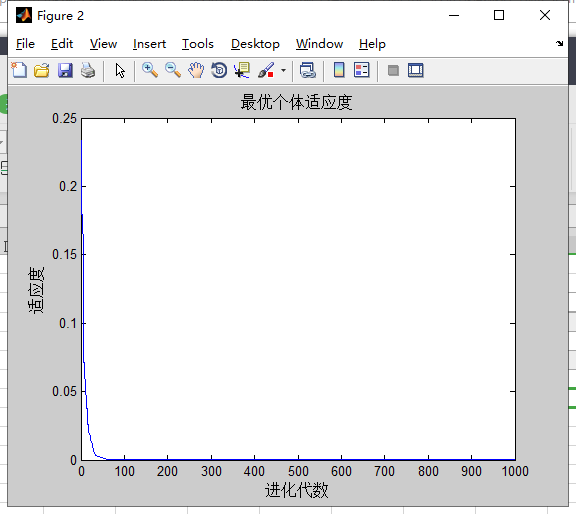
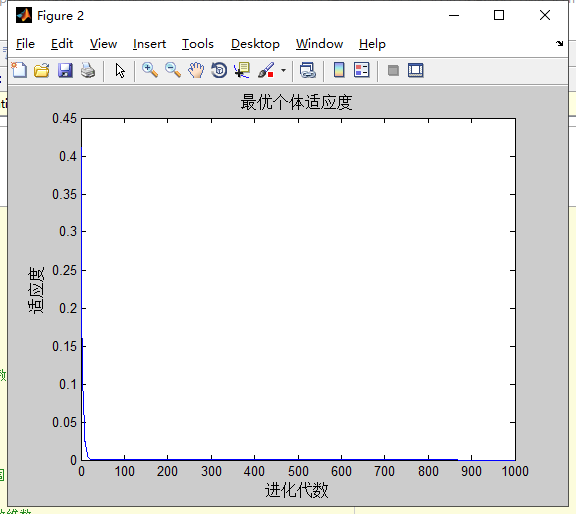
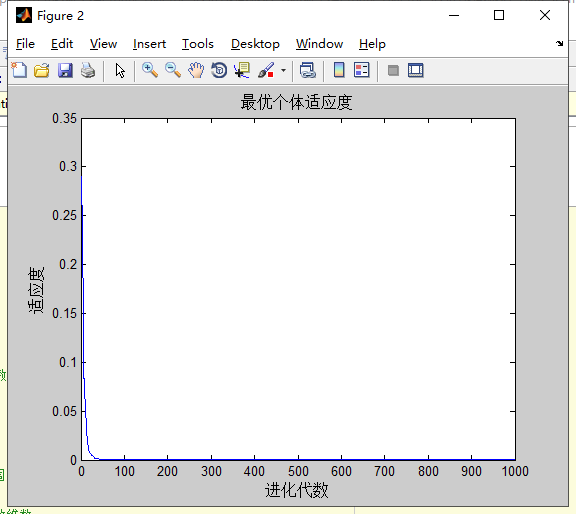
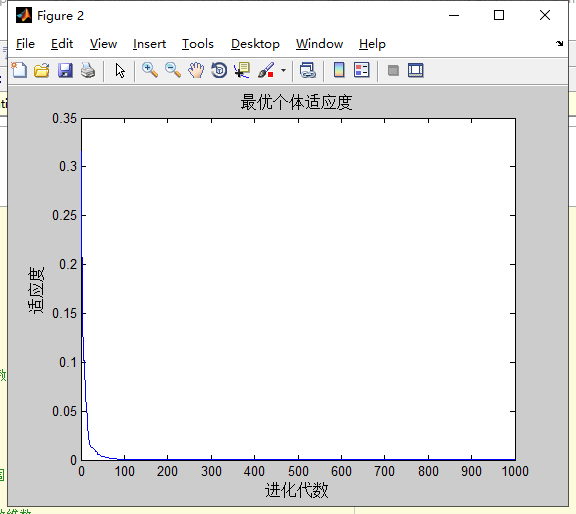
 对Griewank的计算结果：

 

 

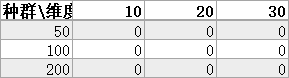
 分析：，

种群和维度不会影响粒子群算法对Griewank寻优的结果。sizepop越大，搜索的精度越高，搜索的稳定性越好，但收敛速度较慢，种群规模小可以减少运行时间。

当维度越大时，越难以达到理论的最优解。