浅入 dancing links x(舞蹈链算法)
abastract:利用dancing links 解决精确覆盖问题,例如数独,n皇后问题;以及重复覆盖问题。
要学习dacning links 算法,首先要先了解该算法适用的问题,精确覆盖问题和重复覆盖问题等,下面先了解精确覆盖问题和重复覆盖问题。
精确覆盖问题
何为精确覆盖问题
在一个全集X中若干子集的集合为S,精确覆盖(Exactcover)是指,S的子集S*,满足X中的每一个元素在S*中恰好出现一次。
定义
S*中任意两个集合没有交集,即X中的元素在S*中出现最多一次
S*中集合的全集为X,即X中的元素在S*中出现最少一次
合二为一,即X中的元素在S*中出现恰好一次。
N={}
O={1,3}
E={2,4}
P={2,3}.
其中一个子集{O,E}是X的一个精确覆盖,因为O={1,3}而E={2,4}的并集恰好是X={1,2,3,4}。同理,{N,O,E}也是X.的一个精确覆盖。空集并不影响结论。
精确覆盖问题的表示方式
一般的,我们用一个集合s包含s中的元素的单向关系表示精确覆盖问题。常用的有以下两种方法:
- 矩阵表示法
包含关系可以用一个关系矩阵表示。.矩阵每行表示S的一个子集,每列表示X中的一个元素。矩阵行列交点元素为1表示对应的元素在对应的集合中,不在则为0。
通过这种矩阵表示法,求一个精确覆盖转化为求矩阵的若干个行的集合,使每列有且仅有一个1。同时,该问题也是精确覆盖的典型例题之一。
下表为其中一个例子:
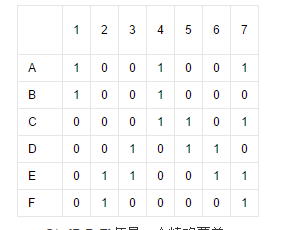
S*={B,D,F}便是一个精确覆盖。
- 图论表示法
可将精确覆盖问题转化为一个二分图,左侧为集合,右侧为元素,左侧集合若与右侧元素有包含关系则连边,通过将左侧节点与其所有边保留与否求解一个右侧的每一个节点恰好有一条边的匹配。
重复覆盖问题
即选取一个01矩阵中的几行,使这几行组成的新矩阵的每一列至少有一个1。 该问题在精确覆盖问题上减少了一个约束条件。
接下来就是dancing links x算法了。
Dancing Links X 算法
历史
X算法是高德纳提出的解决精确覆盖问题的算法,而dancing links X算法则是DonKnuth(《计算机程序设计艺术》的作者)提出的对X算法的一种高效实现,这种实现建立在如上所说的矩阵表示法上。
算法思想
由如上精确覆盖问题的矩阵表示法中,我们知道dancing links x 是用来求解一个 01矩阵中选取哪几行可以使得这几行每一列都有且仅有一个1(就是每个元素在这几个子集里有且仅有出现过一次)。
先不管他的实际意义,我们需要做的就是在一个01矩阵的选取某几行使之符合上述条件。
我们很容易就想到枚举,然后判断符不符合条件,但是这个做法实在是太消耗时间。
dacing links x就是一个高效的求解该类问题的算法,而这种算法,基于交叉十字循环双向链的数据结构。
例如:如下的矩阵
就包含了这样一个集合(第1、4、5行)
如何利用给定的矩阵求出相应的行的集合呢?我们采用回溯法
先假定选择第1行,如下所示:
如上图中所示,红色的那行是选中的一行,这一行中有3个1,分别是第3、5、6列。
由于这3列已经包含了1,故,把这三列往下标示,图中的蓝色部分。蓝色部分包含3个1,分别在2行中,把这2行用紫色标示出来
根据定义,同一列的1只能有1个,故紫色的两行,和红色的一行的1相冲突。
那么在接下来的求解中,红色的部分、蓝色的部分、紫色的部分都不能用了,把这些部分都删除,得到一个新的矩阵
行分别对应矩阵1中的第2、4、5行
列分别对应矩阵1中的第1、2、4、7列
于是问题就转换为一个规模小点的精确覆盖问题
在新的矩阵中再选择第1行,如下图所示
还是按照之前的步骤,进行标示。红色、蓝色和紫色的部分又全都删除,导致新的空矩阵产生,而红色的一行中有0(有0就说明这一列没有1覆盖)。说明,第1行选择是错误的
那么回到之前,选择第2行,如下图所示
按照之前的步骤,进行标示。把红色、蓝色、紫色部分删除后,得到新的矩阵
行对应矩阵2中的第3行,矩阵1中的第5行
列对应矩阵2中的第2、4列,矩阵1中的第2、7列
由于剩下的矩阵只有1行,且都是1,选择这一行,问题就解决
于是该问题的解就是矩阵1中第1行、矩阵2中的第2行、矩阵3中的第1行。也就是矩阵1中的第1、4、5行()
(例子引用自http://www.cnblogs.com/grenet/p/3145800.html)
而对于重复覆盖问题,在选定某一行之后只需删除该行含1的所在列,并不需要再删除所在列上含1的行。
2016-08-21 21:00:15
Example1:HUST 1017
裸精确覆盖问题,问题如下:
1017 - Exact cover
题目描述:
There is an N*M matrix with only 0s and 1s, (1 <= N,M <= 1000). An exact cover is a selection of rows such that every column has a 1 in exactly one of the selected rows. Try to find out the selected rows.输入There are multiply test cases. First line: two integers N, M; The following N lines: Every line first comes an integer C(1 <= C <= 100), represents the number of 1s in this row, then comes C integers: the index of the columns whose value is 1 in this row.输出First output the number of rows in the selection, then output the index of the selected rows. If there are multiply selections, you should just output any of them. If there are no selection, just output "NO".
样例输入
6 7
3 1 4 7
2 1 4
3 4 5 7
3 3 5 6
4 2 3 6 7
2 2 7
样例输出
3 2 4 6
提示来源
dupeng
裸精确覆盖问题,直接用dancing links 做。
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 #define clrlow(x) memset(x,-1,sizeof(x)) 6 #define maxnode 1001010 7 #define maxn 1010 8 using namespace std; 9 struct DLX{ 10 int n,m; 11 int U[maxnode],D[maxnode],L[maxnode],R[maxnode],col[maxnode],row[maxnode]; 12 int H[maxn]; 13 int ansed,ans[maxn],size; 14 void init(int _n,int _m) 15 { 16 n=_n; 17 m=_m; 18 for(int i=0;i<=m;i++) 19 { 20 U[i]=i; 21 D[i]=i; 22 L[i]=i-1; 23 R[i]=i+1; 24 col[i]=i; 25 row[i]=0; 26 } 27 L[0]=m; 28 R[m]=0; 29 size=m; 30 clrlow(H); 31 clr(ans); 32 ansed=0; 33 return ; 34 } 35 void push(int r,int c) 36 { 37 size++; 38 D[size]=D[c]; 39 U[size]=c; 40 U[D[c]]=size; 41 D[c]=size; 42 row[size]=r; 43 col[size]=c; 44 if(H[r]<0) 45 { 46 H[r]=size; 47 R[size]=L[size]=size; 48 } 49 else 50 { 51 L[size]=H[r]; 52 R[size]=R[H[r]]; 53 L[R[H[r]]]=size; 54 R[H[r]]=size; 55 } 56 } 57 void del(int c) 58 { 59 R[L[c]]=R[c]; 60 L[R[c]]=L[c]; 61 for(int i=D[c];i!=c;i=D[i]) 62 for(int j=R[i];j!=i;j=R[j]) 63 { 64 D[U[j]]=D[j]; 65 U[D[j]]=U[j]; 66 } 67 return ; 68 } 69 void reback(int c) 70 { 71 for(int i=U[c];i!=c;i=U[i]) 72 for(int j=L[i];j!=i;j=L[j]) 73 { 74 D[U[j]]=j; 75 U[D[j]]=j; 76 } 77 R[L[c]]=c; 78 L[R[c]]=c; 79 return ; 80 } 81 bool dancing(int dep) 82 { 83 if(R[0]==0) 84 { 85 ansed=dep; 86 return true; 87 } 88 int c=R[0]; 89 del(c); 90 for(int i=D[c];i!=c;i=D[i]) 91 { 92 ans[dep]=row[i]; 93 for(int j=R[i];j!=i;j=R[j]) 94 del(col[j]); 95 if(dancing(dep+1)) 96 return true; 97 for(int j=L[i];j!=i;j=L[j]) 98 reback(col[j]); 99 } 100 return false; 101 } 102 }dlx; 103 int main() 104 { 105 int n,m,p,k; 106 while(scanf("%d%d",&n,&m)==2) 107 { 108 dlx.init(n,m); 109 for(int i=1;i<=n;i++) 110 { 111 scanf("%d",&p); 112 for(int j=1;j<=p;j++) 113 { 114 scanf("%d",&k); 115 dlx.push(i,k); 116 } 117 } 118 if(!dlx.dancing(0)) 119 printf("NO\n"); 120 else 121 { 122 printf("%d",dlx.ansed); 123 for(int i=0;i<dlx.ansed;i++) 124 printf(" %d",dlx.ans[i]); 125 printf("\n"); 126 } 127 } 128 return 0; 129 }
除此之外,运用这个dancing links 的这个模板,还可以解决数独,n皇后问题。
浅谈数独解法
我们在做数独时一般会使用枚举法。在某个格子枚举当前情况下的所有可填入数字,而在枚举其中一个可填入数字后递归到下一层,也就是下一个格子,枚举上一个格子数字确定下来的九宫格在该格子的所有可填入数字,以此类推。直到九宫格完全填满时,这时候的解为该九宫格的一个可行解,可继续递归返回上一层寻找下一个可行解。这个做法效率不错,但是若直接枚举,写起来就又臭又长(好吧我承认其实DLX也挺长的),若九宫格过于稀疏,该做法的时间效率也会指数级上升。我们选择用DLX把每一个已填格子和未填格子的信息转化成行,接下来dance一遍找出符合条件的行,再转化回九宫格信息,就是一个可行解了。最多729行进行DLX(9*9*9,后面你会明白的),速度较直接枚举也快很多,除去DLX的结构体,其他代码长度也比直接枚举短很多(打模板比较快hhh)。
那么怎么把九宫格上的信息转化成行呢? 首先数独中可行的解需满足:每一行,每一列,每一个宫里面不能有相同的数字,且只能使用1-9这九个数字。
把它转化为符合精确覆盖问题的条件,即为:
- 每一个格只能填一个数字。
- 每个数字在每一行只能出现一次。
- 每个数字在每一列只能出现一次。
- 每个数字在每一宫只能出现一次。
对于第一个条件:
第一列表示填入(1,1)这一格。
第二列表示填入(1,2)这一格。
第三列表示填入(1,3)这一格。
……
第(m-1)*9+n列表示填入(m,n)这一格。(1<=m<=9,1<=n<=9)
……
第9*9-1列表示填入(9,8)这一格。
第9*9列表示填入(9,9)这一格。
设inf1=81;
以此类推……
第二个条件:
第inf+1列表示在第一行填入1。
第inf+2列表示在第一行填入2。
第inf+3列表示在第一行填入3。
……
第inf+(n-1)*9+m列表示在第n行填入m(1<=n<=9,1<=m<=9)。
……
第inf+9*9表示在第九行填入9。
设inf2=inf1+81;
对于第三个条件也是如此,inf3=inf2+81;
对于第四个条件,inf4=inf3+81;
至此,已经把所有的条件都转化成了列。
而对于一个有数字的格子(假设位于(m,n)数字为k,位于第p宫)只需把它转化为一行,该行于(m-1)*9+n,inf1+(m-1)*9+k,inf2+(n-1)*9+k,inf3+(p-1)*9+k这四列为1,其余为0。
对于一个没有数字的格子(假设位于(m',n')第p'宫),则需把他转化为九行,分别代表在这一格填入1-9各个数字,每一列的填列原理和有数字的格子一样。
在把所有的格子转化完毕后,先把所有确定的有数字的格子的行以及该行含1的列以及该列上含1的行从矩阵中删除,然后dance一遍,找出符合的行,再把行转化成每个格子的信息,填入九宫格中,就是符合的一个解了。
2016-08-27 17:07:53
n皇后解法
类似于数独问题,在n皇后问题中,不冲突的n皇后的棋盘上符合以下五个个条件:
- 每一个格子最多只能有一个皇后。
- 每一行最多只能有一个皇后。
- 每一列最多只能有一个皇后。
- 每一个从左上往右下的斜边最多只能有一个皇后。
- 每一个从右上往左下的斜边最多只能有一个皇后。
这五个条件看起来不太好用dlx的做法去做,但如果把整个棋盘中有皇后的位置用1表示,没有皇后的位置用1表示,则可以转化为:
- 每个格子只能填一个数字。
- 每一行有且仅能填一个1。
- 每一列有且仅能填一个1。
- 每一个从左上往右下的斜边有且仅能填一个1。
- 每一个从右上往左下的斜边有且仅能填一个1。
按照数独的过程进行DLX,找出填1的行数大于等于n的解。等于n的解即为n皇后问题的解,大于n的解删去几行使填1的行数为n即为n皇后问题的解。
重复覆盖问题
顾名思义,即为在01矩阵中,选出几行,使得在这几行组成的新矩阵中,每一列都有1。
下面是hdu上一个重复覆盖的二分问题,并且给出重复覆盖问题的代码部分:
Example2:hdu 2295
Radar
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2280 Accepted Submission(s): 897
Each of the last M lines consists of the coordinate of a radar station.
All coordinates are separated by one space.
Technical Specification
1. 1 ≤ T ≤ 20
2. 1 ≤ N, M ≤ 50
3. 1 ≤ K ≤ M
4. 0 ≤ X, Y ≤ 1000
该题用二分查找radar的半径,然后用重复覆盖的DLX进行最多选取k行该半径是否完全覆盖所有城市的判断(f()函数和dep一起判断),最后精确到小数点后六位。
#include<cstdio> #include<iostream> #include<cstring> #include<cmath> #define clr(x) memset(x,0,sizeof(x)) #define clrlow(x) memset(x,-1,sizeof(x)) #define maxnode 3000 #define maxn 60 using namespace std; struct DLX//dancing links { int U[maxnode],D[maxnode],L[maxnode],R[maxnode],col[maxnode],row[maxnode];//元素上下左右对应列对应行的指针 int S[maxn],H[maxn],V[maxn];//S为每列元素个数,H指向每行末尾的元素,V是dep()函数的标记数组。 int n,m,size,all;//all为解的行数的最大值 void init(int _n,int _m,int _all) { n=_n; m=_m; all=_all; for(int i=0;i<=m;i++) { L[i]=i-1; R[i]=i+1; U[i]=i; D[i]=i; row[i]=0; col[i]=i; } clr(S); clrlow(H); L[0]=m; R[m]=0; size=m; return ; } //初始化 void push(int r,int c) { D[++size]=D[c]; col[size]=U[size]=c; U[D[c]]=size; D[c]=size; row[size]=r; S[c]++; if(H[r]<0) { H[r]=L[size]=R[size]=size; } else { L[size]=H[r]; R[size]=R[H[r]]; L[R[H[r]]]=size; R[H[r]]=size; } return ; } //加入元素 void del(int c) { S[col[c]]--; for(int i=D[c];i!=c;i=D[i]) { R[L[i]]=R[i]; L[R[i]]=L[i]; S[col[i]]--; } return ; } //删除一列 void reback(int c) { for(int i=U[c];i!=c;i=U[i]) { S[col[R[L[i]]=L[R[i]]=i]]++; } S[col[c]]++; return ; } //恢复一列 int dep( ) { clr(V); int deep=0; for(int i=R[0];i!=0;i=R[i]) if(!V[i]) { deep++; for(int j=D[i];j!=i;j=D[j]) for(int k=R[j];k!=j;k=R[k]) V[col[k]]=1; } return deep; } //之后到达的最大深度 //d为当前深度 bool dancing(int d) { if(d+dep()>all) return false; int c=R[0]; if(c==0) { return d<=all; } for(int i=R[0];i!=0;i=R[i]) if(S[i]<S[c]) c=i; for(int i=D[c];i!=c;i=D[i]) { del(i); for(int j=R[i];j!=i;j=R[j]) del(j); if(dancing(d+1)) return true; for(int j=L[i];j!=i;j=L[j]) reback(j); reback(i); } return false; } //dancing }dlx; struct point { int x,y; }station[maxn],city[maxn]; double dis(point a,point b) { return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y); } int main() { int n,m,k,kase; double lt,rt,mid; double eps=1e-8; scanf("%d",&kase); while(kase--) { scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++) scanf("%d%d",&city[i].x,&city[i].y); for(int i=1;i<=m;i++) scanf("%d%d",&station[i].x,&station[i].y); lt=0; rt=1e8; while(rt-lt>=eps) { dlx.init(m,n,k); mid=(rt+lt)/2; for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) if(dis(city[j],station[i])<mid*mid-eps) dlx.push(i,j); if(dlx.dancing(0)) rt=mid-eps; else lt=mid+eps; } printf("%.6lf\n",lt); } return 0; }
FZU上一道练手题
Problem 1686 神龙的难题
Accept: 717 Submit: 2140
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
这是个剑与魔法的世界.英雄和魔物同在,动荡和安定并存.但总的来说,库尔特王国是个安宁的国家,人民安居乐业,魔物也比较少.但是.总有一些魔物不时会进入城市附近,干扰人民的生活.就要有一些人出来守护居民们不被魔物侵害.魔法使艾米莉就是这样的一个人.她骑着她的坐骑,神龙米格拉一起消灭干扰人类生存的魔物,维护王国的安定.艾米莉希望能够在损伤最小的前提下完成任务.每次战斗前,她都用时间停止魔法停住时间,然后米格拉他就可以发出火球烧死敌人.米格拉想知道,他如何以最快的速度消灭敌人,减轻艾米莉的负担.
 Input
Input
数据有多组,你要处理到EOF为止.每组数据第一行有两个数,n,m,(1<=n,m<=15)表示这次任务的地区范围. 然后接下来有n行,每行m个整数,如为1表示该点有怪物,为0表示该点无怪物.然后接下一行有两个整数,n1,m1 (n1<=n,m1<=m)分别表示米格拉一次能攻击的行,列数(行列不能互换),假设米格拉一单位时间能发出一个火球,所有怪物都可一击必杀.
 Output
Output
输出一行,一个整数,表示米格拉消灭所有魔物的最短时间.
 Sample Input
Sample Input
 Sample Output
Sample Output
 Source
Source
FOJ月赛-2009年2月- TimeLoop
依旧是重复覆盖问题模板
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define clr(x) memset(x,0,sizeof(x)) 5 #define clrlow(x) memset(x,-1,sizeof(x)) 6 #define maxm (15*15+10) 7 #define maxn (15*15+10) 8 #define maxnode maxn*maxm 9 #define INF 1000000000 10 using namespace std; 11 struct DLX 12 { 13 int size,n,m; 14 int D[maxnode],U[maxnode],L[maxnode],R[maxnode],row[maxnode],col[maxnode]; 15 int H[maxn],S[maxm]; 16 int ansed; 17 void init(int _n,int _m) 18 { 19 n=_n; 20 m=_m; 21 size=m; 22 for(int i=0;i<=m;i++) 23 { 24 D[i]=i; 25 U[i]=i; 26 R[i]=i+1; 27 L[i]=i-1; 28 row[i]=0; 29 col[i]=i; 30 S[i]=0; 31 } 32 L[0]=m; R[m]=0; 33 for(int i = 1;i <= n;i++)H[i] = -1; 34 ansed=INF; 35 return ; 36 } 37 void push(int r,int c) 38 { 39 ++S[col[++size]=c]; 40 row[size]=r; 41 D[size]=D[c]; 42 U[size]=c; 43 U[D[c]]=size; 44 D[c]=size; 45 if(H[r]<0) 46 { 47 L[size]=R[size]=size; 48 H[r]=size; 49 } 50 else 51 { 52 R[size]=R[H[r]]; 53 L[size]=H[r]; 54 L[R[H[r]]]=size; 55 R[H[r]]=size; 56 } 57 return; 58 } 59 void del(int p) 60 { 61 for(int i=D[p];i!=p;i=D[i]) 62 { 63 R[L[i]]=R[i]; 64 L[R[i]]=L[i]; 65 } 66 return ; 67 } 68 void remove(int p) 69 { 70 for(int i=U[p];i!=p;i=U[i]) 71 { 72 R[L[i]]=L[R[i]]=i; 73 } 74 return ; 75 } 76 bool v[maxm]; 77 int dis() 78 { 79 int ans=0; 80 for(int i=1;i<=m;i++) v[i]=0; 81 for(int i=R[0];i!=0;i=R[i]) 82 if(!v[i]) 83 { 84 ans++; 85 for(int j=D[i];j!=i;j=D[j]) 86 for(int k=R[j];k!=j;k=R[k]) 87 v[col[k]]=1; 88 } 89 return ans; 90 } 91 void dancing(int dep) 92 { 93 if(dep+dis()>=ansed) return; 94 if(R[0]==0) 95 { 96 if(dep<ansed) ansed=dep; 97 return ; 98 } 99 int c=R[0]; 100 for(int i=R[0];i!=0;i=R[i]) 101 if(S[i]<S[c]) 102 c=i; 103 for(int i=D[c];i!=c;i=D[i]) 104 { 105 del(i); 106 for(int j=R[i];j!=i;j=R[j]) 107 del(j); 108 dancing(dep+1); 109 for(int j=L[i];j!=i;j=L[j]) 110 remove(j); 111 remove(i); 112 } 113 return ; 114 } 115 }dlx; 116 int n,m,n1,m1,a[maxn][maxm],num[maxn][maxm],inf; 117 int main() 118 { 119 while(scanf("%d%d",&n,&m)!=EOF) 120 { 121 inf=0; 122 clr(a); 123 clr(num); 124 for(int i=1;i<=n;i++) 125 for(int j=1;j<=m;j++) 126 { 127 scanf("%d",&a[i][j]); 128 if(a[i][j]==1) num[i][j]=(++inf); 129 } 130 dlx.init(n*m,inf); 131 scanf("%d%d",&n1,&m1); 132 inf=0; 133 for(int i=1;i<=n;i++) 134 for(int j=1;j<=m;j++) 135 { 136 inf++; 137 for(int k=i;k<i+n1 && k<=n;k++) 138 for(int l=j;l<j+m1 && l<=m;l++) 139 if(num[k][l]) 140 dlx.push(inf,num[k][l]); 141 } 142 dlx.dancing(0); 143 printf("%d\n",dlx.ansed); 144 } 145 return 0; 146 }
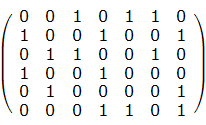
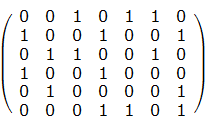
![clip_image002[4] clip_image002[4]](http://images0.cnblogs.com/blog/93227/201306/20141206-3b4bd7db79394066a3b1fb416caab2f5.png)
![clip_image002[6] clip_image002[6]](http://images0.cnblogs.com/blog/93227/201306/20141210-51c3f91ceebe404d89c8b70adf1b9909.png)
![clip_image002[8] clip_image002[8]](http://images0.cnblogs.com/blog/93227/201306/20144122-518a2ef670d0491794eebaa7da2f2f98.png)
![clip_image002[10] clip_image002[10]](http://images0.cnblogs.com/blog/93227/201306/20144122-a9c55df3ed704ed78f1f471a3d82de05.png)
