广义线性模型
指数分布族
如果一类分布可以写成如下的形式,那么它就是属于指数分布族的:
P(y;η) = b(y)exp(ηTT(y) - a(η)) (1)
这里η叫做分布的自然参数(natural parameter),或者叫标准参数(canonical parameter);T(y)是充分统计量( sufficient statistic),对于我们考虑的大多数分布,T(y)=y;然后a(η)叫做log partition function。实际上,伯努利分布和正态分布都属于指数分布族,分析如下。
Bernoulli分布
伯努利概率分布如下:
P(y;φ) = φy(1 - φ)1-y = exp(ylog(φ) + (1 - y)log(1 - φ)) = exp(ylog(φ/(1-φ)) + log(1-φ)) (2)
(2)式对比(1)式,显然有
T(y) = y; η = log(φ/(1-φ)); a(η) = -log(1-φ) = 1/(1+exp(η)) // sigmoid
Gaussian分布
高斯概率分布如下:
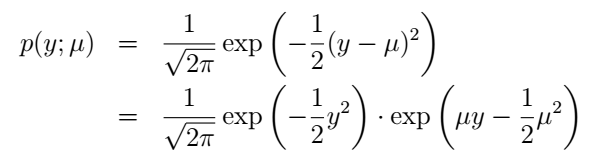
则有:
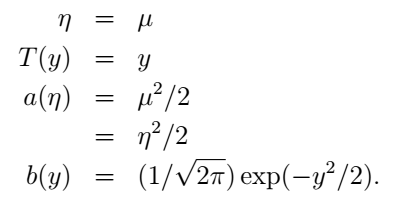
由以上分析可知,伯努利和高斯分布都属于指数分布族。
广义线性模型
对于回归问题,如果满足以下三个条件,即可应用广义线性模型解决:
y的条件概率属于指数分布族
- 给定x 广义线性模型的目标是 求解
, 不过由于 很多情况下
所以我们的目标变成了
, 也即 我们希望拟合函数为
( 备注: 这个条件在 线性回归 和 逻辑回归中都满足, 例如 逻辑回归中
)
- 自然参数
与 x是线性关系 :
(
为向量时
)
广义线性模型推导出线性回归:
step1:
step2: 由假设2 得到:

广义线性模型推导出逻辑回归:
step1:
step2: 与上面同理
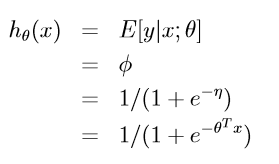
广义线性模型推导出 Softmax Regression:

