矩阵乘法内核优化CUDA杂谈

矩阵乘法内核优化CUDA杂谈

矩阵乘法内核优化CUDA杂谈

How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog

https://siboehm.com/articles/22/CUDA-MMM

在这篇文章中，我将迭代优化用CUDA编写的矩阵乘法的实现。我的目标不是构建cuBLAS的替代品，而是深入了解用于现代深度学习的GPU最重要的性能特征。这包括整合全局内存访问、共享内存缓存和占用优化等。

GPU上的矩阵乘法可能是目前存在的最重要的算法，因为它几乎构成了大型深度学习模型训练和推理过程中的所有FLOP。那么，编写一个高性能的CUDA需要多少工作呢。从头开始？我将从一个简单的内核开始，逐步应用优化，直到我们达到cuBLAS（NVIDIA的官方矩阵库）性能的95%以内（在好的一天）：

内核	GFLOPs/s	相对于cuBLAS的性能
1: Naive	309.0	1.3%
2: GMEM Coalescing	1986.5	8.5%
3: SMEM Caching	2980.3	12.8%
4: 1D Blocktiling	8474.7	36.5%
5: 2D Blocktiling	15971.7	68.7%
6: Vectorized Mem Access	18237.3	78.4%
9: Autotuning	19721.0	84.8%
10: Warptiling	21779.3	93.7%
0: cuBLAS	23249.6	100.0%

内核1：朴素的实现

在CUDA编程模型中，计算按三级层次进行排序。每次调用CUDA内核都会创建一个由多个块组成的新网格。每个块最多由1024个单独的线程组成。同一块中的线程可以访问相同的共享内存区域（SMEM）。

块中的线程数可以使用通常称为blockDim的变量进行配置，该变量是一个由三个整数组成的向量。该向量的条目指定了blockDim.x、blockDim.y和blockDim.z的大小，如下所示：

 

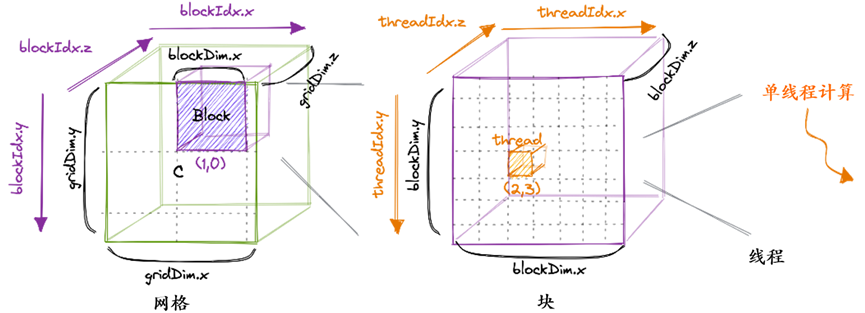
同样，网格中的块数也可以使用gridDim变量进行配置。当我们从主机启动一个新内核时，它会创建一个网格，其中包含指定的块和线程。从这里开始，我将只谈论2D网格和块，部分原因是3D结构很少使用，而且3D绘图太难了。重要的是要记住，我们刚才谈到的线程层次结构主要涉及程序的正确性。

对于我们的第一个内核，我们将使用网格、块和线程层次结构在结果矩阵C中为每个线程分配一个唯一的条目。然后，该线程将计算a的相应行和B的相应列的点积，并将结果写入C。由于C的每个位置只由一个线程写入，我们不必进行同步。我们将这样启动内核：

//根据需要创建尽可能多的块来映射所有C

dim3 gridDim(CEIL_DIV(M, 32), CEIL_DIV(N, 32), 1);

//32*32=1024个线程/块

dim3 blockDim(32, 32, 1);

//在设备上启动内核的异步执行

//函数调用在主机上立即返回

sgemm_naive<<<gridDim, blockDim>>>(M, N, K, alpha, A, B, beta, C);

CUDA代码是从单线程的角度编写的。在内核的代码中，我们访问blockIdx和threadIdx内置变量。这些将根据访问它们的线程返回不同的值。

__global__ void sgemm_naive(int M, int N, int K, float alpha, const float *A,

const float *B, float beta, float *C) {

// 计算该线程在C中负责的位置

const uint x = blockIdx.x * blockDim.x + threadIdx.x;

const uint y = blockIdx.y * blockDim.y + threadIdx.y;

 

// 当M或N不是32的倍数时，“if”条件是必要的。

if (x < M && y < N) {

float tmp = 0.0;

for (int i = 0; i < K; ++i) {

tmp += A[x * K + i] * B[i * N + y];

}

// C = α*(A@B)+β*C

C[x * N + y] = alpha * tmp + beta * C[x * N + y];

}

}

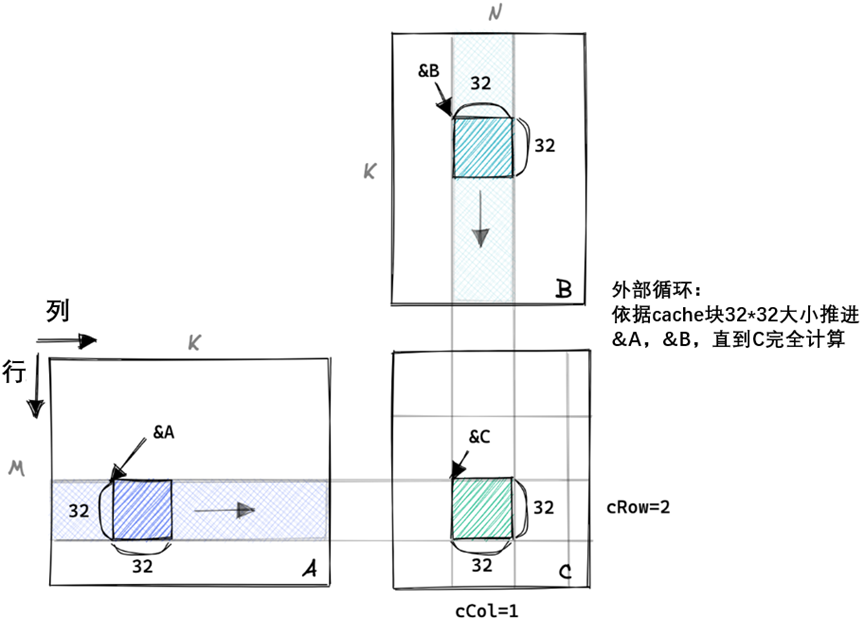
要可视化这个简单的内核：

 

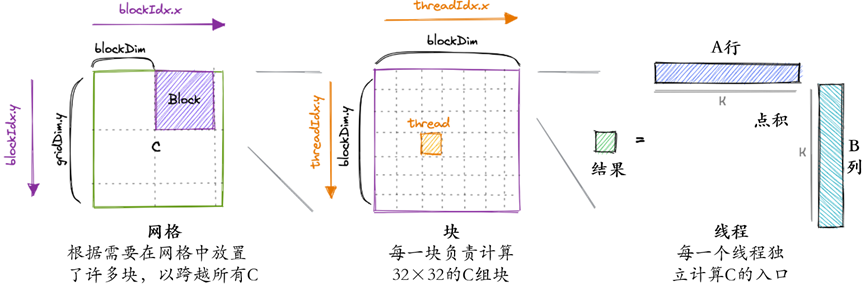
这个内核在我的A6000 GPU上处理三个

fp32矩阵大约需要0.5秒。让我们做一些非实现特定的计算：

最快运行时间的下限

对于两个4092²矩阵的矩阵乘法，然后加上一个

矩阵（以制作GEMM）：

总FLOPS：

GFLOPS

2*4092³+4092²=137立方英尺

要读取的总数据（最小值！）：

 

要存储的总数据：

 

为1TB/s，那么他们谈论的是全局内存的容量和带宽。稍后我们将讨论GPU上的其他内存区域，比如共享内存，它在物理上是不同的，具有非常不同的性能特征。假设它有足够大的缓存。在整个计算过程中，cuBLAS内核总共加载了500MB的GMEM。稍后我们将看到增加算术强度如何使我们实现如此低的访问量。让我们计算一些内核性能的上限。GPU的广告显示，其fp32计算吞吐量为30TFLOP/s，全局内存带宽为768GB/s。如果我们达到了这些数字，提醒一下，峰值FLOPS是一个简化的指标，因为它取决于指令组合。如果你选择的FLOP是DIV，你就不可能达到30TFLOP/s。但是，由于matmul主要使用FMA指令，这往往是最快的FLOP，我们很有可能真正接近峰值FLOP值。带宽的情况类似：只有当访问模式适合硬件时，才能达到峰值带宽。计算需要4.5ms，内存传输需要0.34ms。因此，在我们的餐巾纸数学中，计算所需的时间比内存访问多10倍。

这意味着我们最终优化的内核将受到计算限制，只要我们最终必须传输小于278MB绝对最小内存量的10倍。

现在我们已经计算了fp32 GEMM计算的一些下限，让我们回到手头的内核，找出为什么它比实际速度慢得多。

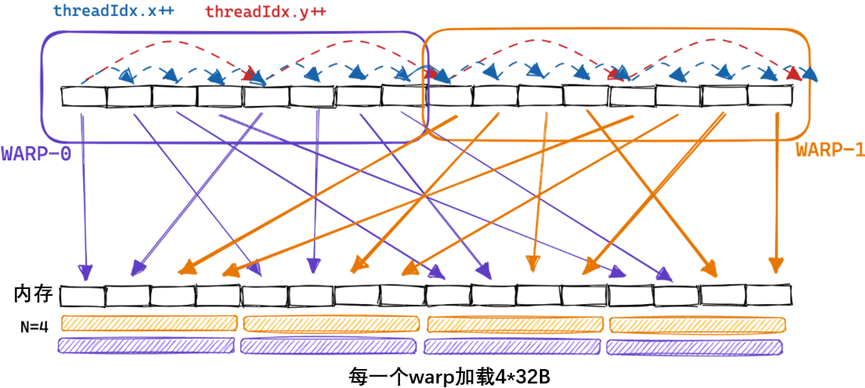
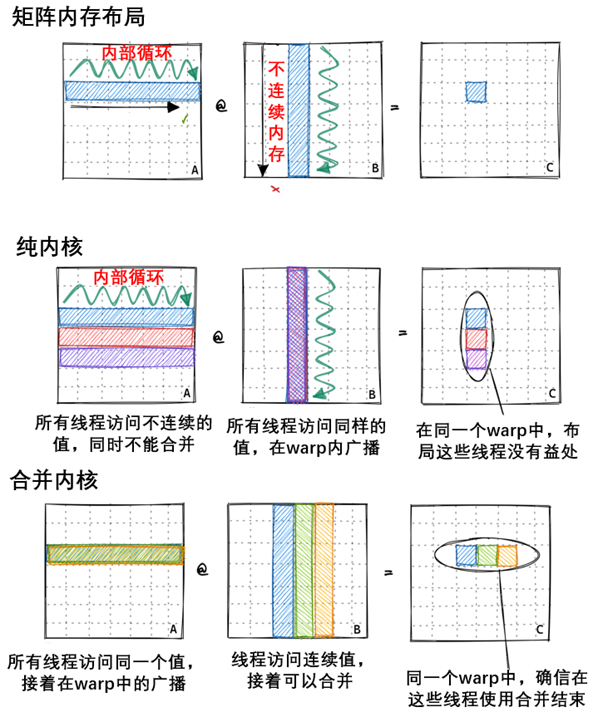
朴素内核的内存访问模式

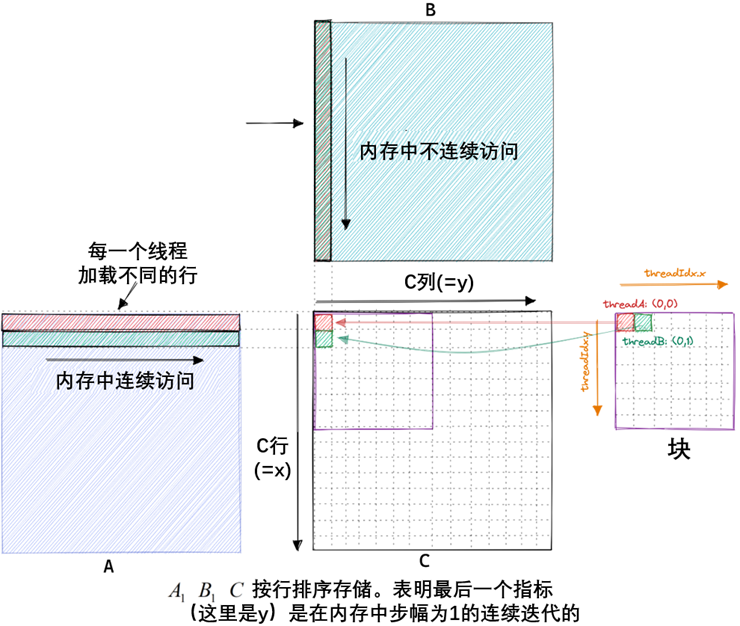
在我们的内核中，同一块中具有ThreadIds (0, 0)和（0,1）的两个线程将加载相同的B列，但加载不同的A行。如果我们假设最坏的情况是零缓存，那么每个线程都必须从全局内存中加载2*4092+1个浮点数。由于我们总共有4092²的线程，这将导致548GB的内存流量。

下面是我们朴素内核的内存访问模式的可视化，以两个线程a（红色）和B（绿色）为例：

  

综上所述，当我在A6000 GPU上运行这个内核时，当乘以两个4092x4092 float32矩阵时，它达到了约300GFLOPs。考虑到A6000被宣传为能够实现近30个TFLOP，情况相当糟糕。为了便于比较，300 GFLOP也大致相当于我在之前关于CPU matmul的文章中使用的2015 Haswell CPU上优化的BLAS库所达到的性能。那么，我们如何才能开始加快速度呢？一种方法是优化内核的内存访问模式，以便将全局内存访问合并为更少的访问。

 

 

参考文献链接

https://siboehm.com/articles/22/CUDA-MMM