机器视觉：摄像机标定技术

机器视觉：摄像机标定技术

https://mp.weixin.qq.com/s/UGkYtGsGsgiiCzsaYlkx4g

空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数，为了得到这些参数而进行的实验与计算的过程称为摄像机标定。

在标定过程中通常要利用数学方法对从数字图像中获得的数据进行处理。通过这些数学处理，可以得到摄像机的内部和外部参数。

一、成像几何模型

四个坐标系

1）图像像素坐标系：表示三维空间物体在图像平面上的投影，像素是离散化的，其坐标原点在CCD图像平面的左上角，u轴平行于CCD平面水平向右，v轴垂直于u轴向下，坐标使用(u, v)来表示。图像宽度W，高度H。

2）图像物理坐标系：坐标原点在CCD图像平面的中心x, y轴分别平行于图像像素坐标系的(u,v)轴，坐标用(x, y)表示。

3）相机坐标系：以相机的光心为坐标系原点，

 ，

 轴平行于图像坐标系的x，y轴，相机的光轴为

 轴，坐标系满足右手法则。相机的光心可理解为相机透镜的几何中心。

4）世界坐标系：用于表示空间物体的绝对坐标，使用

 表示，世界坐标系可通过旋转和平移得到相机坐标系。

 

 

1.世界坐标系

 

2.摄像机坐标系

 

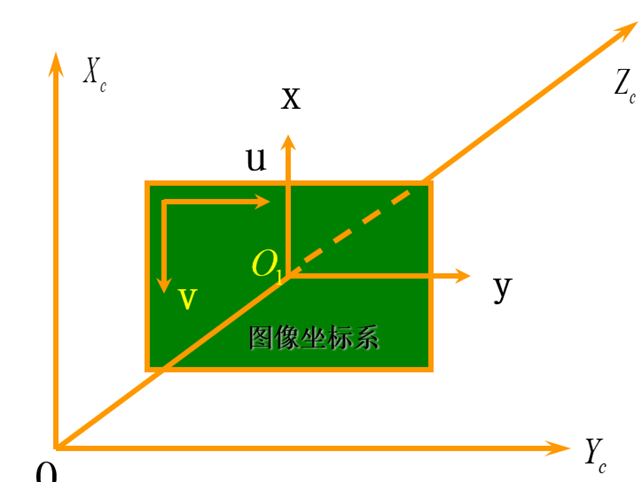
3.图像坐标系

 

4.空间点与像点的非线性关系分析

由于摄像机的光学成像系统与理论模型之间的差异，二维图像存在着不同程度的非线性变形，目标像点与理论成像点相比存在着多种类型的几何畸变.

径向畸变主要是由镜头形状缺陷造成的，是关于摄像机镜头的主光轴对称的。

正向畸变是枕形畸变，负向畸变是桶形畸变，其数学模型为：

 其中，

 为畸变系数。

偏心畸变主要是由光学系统光心与几何中心不一致造成的，即各透镜的光轴中心不能严格共线。

这类畸变既含有径向畸变，又含有切向畸变。

切向畸变的数学模型为：

 其中，

 为切向畸变系数。

薄棱镜畸变是由于镜头设计、制造缺陷或加工安装误差所造成的，如镜头与摄像机像面有很小的倾角等。

这类畸变相当于在光学系统中附加了一个薄棱镜，不仅会引起径向偏差，而且引起切向误差。

其数学模型为：

  其中，

 为薄棱镜畸变参数。

二、典型标定方法

1.传统摄像机标定方法

优点：可以使用于任意的摄像机模型，标定精度高。

不足：标定过程复杂，需要高精度的已知结构信息。在实际应用中很多情况下无法使用标定块。

2.摄像机自标定方法

特点：仅依靠多幅图像之间的对应关系进行标定。

优点：仅需要建立图像之间的对应，灵活性强，潜在应用范围广。

不足：非线性标定，鲁棒性不高。

3.传统的摄像机标定方法

利用已知的景物结构信息。常用到标定块。

 

 

图3-1.平面透视畸变是非线性的：不能使用2D线性变换来描述

•利用最优化算法的标定方法

•利用摄像机变换矩阵的标定方法

•两步法

•双平面标定法

 

基本原理：

  

其中，K为摄像机的内参数矩阵。由于摄像机有5个未知内参数，所以当所摄取得的图象数目大于等于3时，就可以线性唯一求解出K。

 

张正友方法所用的平面模板

4.摄像机自标定方法

利用本质矩阵和基本矩阵的摄像机标定方法；利用主动系统控制摄像机作特定运动的自标定方法（主动视觉标定方法）。

5.基于平面单应矩阵的正交运动方法原理

t(1)、t(2)为摄像机一组正交的平移运动，两个单应矩阵：

 满足：

 五组两正交运动可完全求解5个内参数。

原文链接：

https://blog.csdn.net/m0_53966219/article/details/127695175

自动驾驶从小白到小强12～摄像头标定

https://mp.weixin.qq.com/s/V-6LjNcLDW_GQajdRH9opQ

1.为什么需要摄像头标定

2.摄像头模型

3.透镜畸变

4.车载摄像头参数标定

5.动态标定与静态标定

​1.为什么需要摄像头标定

摄像头在生产过程中存在一致性问题，摄像头以一定的角度和位置安装在车辆上，又存在安装偏差。为了将摄像头采集到的环境数据与现实环境中的真实物体相对应，即找到实际环境中的物体坐标与摄像头生成的图像像素坐标系中的点坐标之间的转换关系，需要对摄像头进行标定。

​

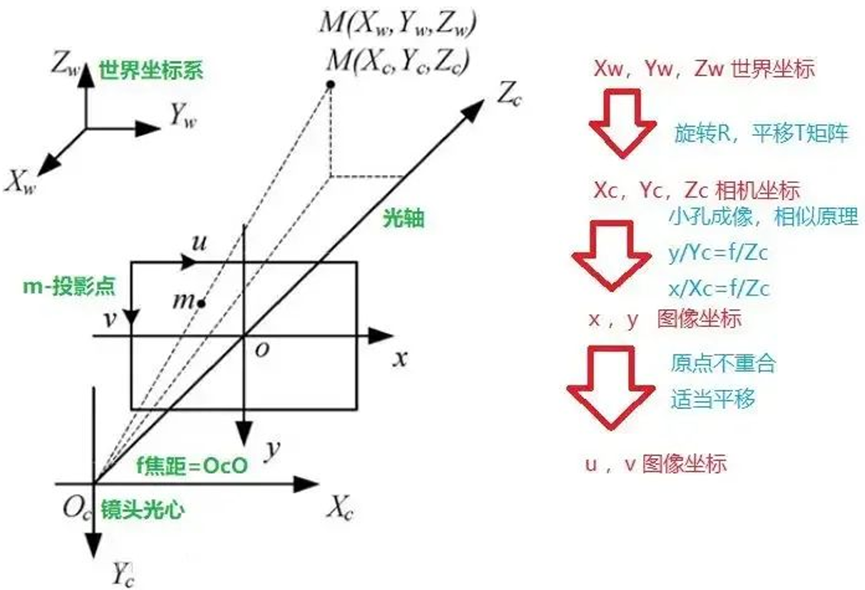
   单目相机的标定主要是建立世界坐标系、摄像机坐标系和图像坐标系之间的关系。

图像坐标系分为图像像素坐标系和图像物理坐标系。

​

图像像素坐标系：图像都是由像素组成的，以图像左上角为原点建立以像素为单位的直接坐标系u-v即图像像素坐标系。像素点01的横坐标u0与纵坐标v0分别是在其图像数组中所在的列数与所在行数。（在OpenCV中u对应x，v对应y）

​

图像物理坐标系：由于(u，v)只代表像素的列数与行数，而像素在图像中的位置并没有用物理单位表示出来，所以，还要建立以物理单位（如毫米mm）表示的图像坐标系x-y。将相机光轴与图像平面的交点（一般位于图像平面的中心处，也称为图像的主点（principal point）定义为该坐标系的原点O1，且x轴与u轴平行，y轴与v轴平行，假设(u0,v0)代表O1在u-v坐标系下的坐标，dx与dy分别表示每个像素在横轴x和纵轴y上的物理尺寸，则图像中的每个像素在u-v坐标系中的坐标和在x-y坐标系中的坐标之间都存在如下的关系：

x=（u-u0）*dx

y=（v-v0）*dy

其中，假设物理坐标系中的单位为毫米，那么dx、dy的单位为:毫米/像素。

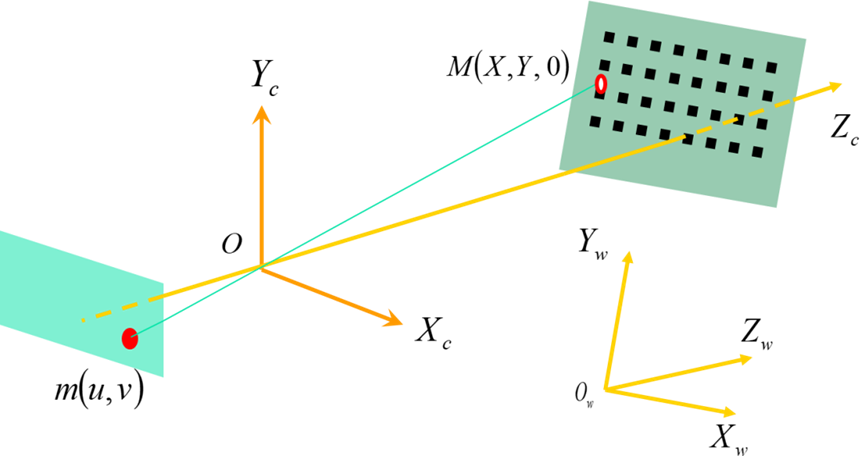
摄像机坐标系：相机成像的几何关系可由下图表示。其中O点为摄像机光心（投影中心），Xc轴和Yc轴与成像平面坐标系的x轴和y轴平行，Zc轴为摄像机的光轴，和图像平面垂直。光轴与图像平面的交点为图像的主点O1，由点O与Xc，Yc，Zc轴组成的直角坐标系称为摄像机的坐标系。OO1为摄像机的焦距。

 

 

世界坐标系：即系统坐标系中的车体坐标系，是为了描述相机的位置而被引入的，如上图中坐标系OwXwYwZw即为世界坐标系。车体与摄像机是刚性连接的，假设车体坐标系中的实物点P坐标为（Xw，Yw，Zw），实物点P在摄像机坐标系中的坐标为（Xc，Yc，Zc），通过平移向量T和旋转矩阵R可以用来表示相机坐标系与世界坐标系的关系。​

 

 

 实际上R和T表示相机相对于车体坐标系的安装角度和安装位置，因此把R和T定义为相机的外部参数。

 

 ​  

 

​2.摄像头模型

理想针孔相机模型（线性模型）：针孔相机模型就是把相机简化成小孔成像，任一点在像平面的投影点都是O（光心，即投影中心）与该点的连线与像平面的交点。通过透视变换投影将摄像机坐标系中的物点P（Xc，Yc，Zc）转换至理想非畸变的图像物理坐标系像点P（x，y），方程如下：

x=f*Xc/Zc

y=f*Yc/Zc

f为摄像头的焦距即OO1的距离。可以想见，这种简化对于精度要求高的情况或者广角相机是不适用的。对图像物理坐标系中像点P（x，y）转换至图像像素坐标系像点P（u，v），方程如下：

u=x/dx + u0

v=y/dy + v0

其中，(u0,v0)为图像像素中心的坐标，即相机光轴与图像平面的交点，dx与dy分别表示每个像素在横轴x和纵轴y上的物理尺寸，由摄像机厂家提供，可以在摄像机说明书上查到，为已知量。车体坐标系中的实物点P坐标为（Xw，Yw，Zw），由摄像机坐标系中物点P（Xc，Yc，Zc）与图像像素坐标系中的像点P（u，v）的变换关系如下：​

 其中，fx=f/dx，fy=f/dy，分别定义为x和y方向的等效焦距，fx、fy、u0、v0等参数只与摄像机和镜头的内部结构有关，因此把fx、fy、u0、v0定义为摄像机内部参数。

当相机为理想的摄像机模型时，物点P（Xw，Yw，Zw）、光心、像点P（u，v）三点在同一直线上。根据这一特点，在摄像机内部参数确定的情况下，可以利用三维空间上的若干个特征点在车体坐标系中的坐标和图像像素坐标系中的坐标建立约束方程，从而求出摄像机的6个外部参数，即摄像机相对于车体的相对姿态（俯仰角、横滚角、航向角）和相对位置（X、Y、Z）。

在实际应用中，因为存在透镜畸变，物点在实际的相机成像平面上生成的像与理想成像之间存在一定光学畸变误差，相机并不能完全精确地按照理想的摄像机模型进行透视投影。

​3.透镜畸变

镜头透镜由于制造精度以及组装工艺的偏差会引入畸变，导致原始图像的失真，因此在摄像头标定时要消除透镜畸变。

镜头透镜的畸变分为径向畸变和切向畸变两类。

径向畸变：顾名思义，径向畸变就是沿着透镜半径方向分布的畸变。光线在真空条件下，没有物质折射和反射，光线的特质为随光源角度和物理特性的直射光。而经过物质参与和阻隔光学光线通道时，光线会随着共性物质的特性和所在环境产生衍射及光学通道扭曲，光线在透镜中心的地方比靠近中心的地方更加弯曲，就会产生径向畸变。这种畸变在普通廉价的镜头中表现更加明显，径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图：

 

 

​

成像仪光轴中心的畸变为0，沿着镜头半径方向向边缘移动，畸变越来越严重。畸变的数学模型可以用主点（principle point）周围的泰勒级数展开式的前几项进行描述，通常使用前两项，即k1和k2，对于畸变很大的镜头，如鱼眼镜头，可以增加使用第三项k3来进行描述，成像仪上某点根据其在径向方向上的分布位置，调节公式为：​

 其中（x，y）为理想状态下的像点P的坐标，（x0，y0）为考虑镜头径向畸变的像点P0的坐标。距离光心越远，径向位移越大，表示畸变也越大，在光心附近，几乎没有偏移。

切向畸变：是由于透镜本身与相机传感器平面（成像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。畸变模型可以用两个额外的参数p1和p2来描述： ​

 其中（x，y）为理想状态下的像点P的坐标，（x0，y0）为考虑镜头切向畸变的像点P0的坐标。

前视单目相机考虑透镜畸变时通常用下面的方程进行表示。

 4.车载相机参数标定

在实际的车载相机应用中，往往忽略摄像机镜头的畸变或者只考虑径向畸变。在车载应用中摄像机的成像误差要求相对宽松，而且待处理目标通常会在图像中心附近出现，因此其位置误差对于车载应用可以满足。另外，不考虑摄像机镜头畸变可以提高系统的实时性，考虑镜头畸变的摄像机模型比理想的摄像机模型复杂，物点和像点之间的转换计算量会大大增加，根据上述的摄像机模型可以把相机参数作为内部参数和外部参数，其中内部参数为fx、fy、u0、v0，外部参数为R和T，实际上R由偏航角θ、俯仰角φ、翻滚角ψ确定，其表达式为：​

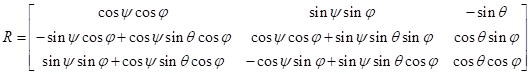
 相机的内部参数可以通过各种相机标定工具箱完成，外部参数可以通过相机模型建立约束方程求解，通过提取多个定标物特征点来求解约束方程的外部参数，在图像像素坐标系中，提取到图像特征点为Pn（un，vn），其中n为定标物的特征点个数，利用这些特征点序列即可建立多个约束方程，特征点尽可能地均匀分布在图像分辨率范围内的各个位置，可以利用线性最小二乘法求出其外部参数的最优解。

​5.动态标定与静态标定

车辆在产线下线时，受限于产线空间、生产节拍等、标定成功率等因素，一般使用静态标定方法。

​它需要使用尺寸已知的标定板，用于建立标定物上坐标已知的点与其图像点之间的对应，利用一定的算法获得相机模型的内外参数。根据标定物的不同可分为三维标定物和平面型标定物。三维标定物可由单幅图像进行标定，标定精度较高，但高精密三维标定物的加工和维护较困难。平面型标定物比三维标定物制作简单，精度易保证，但标定时必须采用两幅或两幅以上的图像。

 

OpenCV（C++）实现相机/图像的畸变校正

https://blog.csdn.net/weixin_42734533/article/details/110201793

主要介绍一下相机的畸变以及如何获取相机的内参以及畸变系数，从而尽可能消除畸变的影响。

 

畸变校正的基本流程

1.采集标定板图像，大约十五张左右；

2.根据使用的标定板确定标定板的内点数，找出标定板的角点坐标

3.进一步提取亚像素角点信息；

4.计算并获取相机的内参矩阵和畸变系数；

5.畸变图像的校正修复

 

0.准备标定板

标定板可以直接从opencv官网上能下载到：

链接: 标定板.

然后直接打印出来即可。

得出标定板的内部行列交点个数：6*9——下面在求解相机参数和畸变系数时会用

 

1.采集标定板图像

附上代码：

#include "opencv2/opencv.hpp"

#include <string>

#include <iostream>

 

#include <conio.h>  //按键事件头文件

#include <iostream>

 

using namespace cv;

using namespace std;

 

int main()

{

    VideoCapture inputVideo(0);

    inputVideo.set(CAP_PROP_FRAME_WIDTH, 960);

    inputVideo.set(CAP_PROP_FRAME_HEIGHT, 480);

    if (!inputVideo.isOpened())

    {

        cout << "Could not open the input video " << endl;

        return -1;

    }

    Mat frame;

    string imgname;

    int f = 1;

    int ch;

    while (1) //Show the image captured in the window and repeat

    {

        inputVideo >> frame;              // read

        if (frame.empty()) break;         // check if at end

        imshow("Camera", frame);

 

        if (_kbhit()) {//如果有按键按下，则_kbhit()函数返回真

           ch = _getch();//使用_getch()函数获取按下的键值

           //cout << ch;

           if (ch == 27)

           {

               imgname = to_string(f++) + ".jpg";

               imwrite(imgname, frame);

          

           }//当按下ESC时循环，ESC键的键值时27.

        }

 

        char key = waitKey(10);

 

    }

    cout << "Finished writing" << endl;

    return 0;

}

获取的图像如下图所示：

2.直接上程序，通过库函数的解算，即可获得相机内参及畸变系数

代码如下：

// CheckerBoardDemo.cpp : 定义控制台应用程序的入口点。

//

 

//#include <stdafx.h>

#include <opencv2\imgproc\types_c.h>

#include<opencv2/opencv.hpp>

#include<iostream>

using namespace cv;

using namespace std;

 

Mat image, img_gray;

int BOARDSIZE[2]{ 6,9 };//棋盘格每行每列角点个数

int main()

{

    vector<vector<Point3f>> objpoints_img;//保存棋盘格上角点的三维坐标

    vector<Point3f> obj_world_pts;//三维世界坐标

    vector<vector<Point2f>> images_points;//保存所有角点

    vector<Point2f> img_corner_points;//保存每张图检测到的角点

    vector<String> images_path;//创建容器存放读取图像路径

 

    string image_path = "F:/Works/C++/openCV/opencv study/Revise/Revise/Project1/*.jpg";//待处理图路径    F:/Works/C++/openCV/opencv study/Revise/Revise/Project1/

    glob(image_path, images_path);//读取指定文件夹下图像

 

    //转世界坐标系

    for (int i = 0; i < BOARDSIZE[1]; i++)

    {

        for (int j = 0; j < BOARDSIZE[0]; j++)

        {

           obj_world_pts.push_back(Point3f(j, i, 0));

        }

    }

 

    for (int i = 0; i < images_path.size(); i++)

    {

        image = imread(images_path[i]);

        cvtColor(image, img_gray, COLOR_BGR2GRAY);

        //检测角点

        bool found_success = findChessboardCorners(img_gray, Size(BOARDSIZE[0], BOARDSIZE[1]),

           img_corner_points,

           CALIB_CB_ADAPTIVE_THRESH | CALIB_CB_FAST_CHECK | CALIB_CB_NORMALIZE_IMAGE);

 

        //显示角点

        if (found_success)

        {

           //迭代终止条件

           TermCriteria criteria(CV_TERMCRIT_EPS | CV_TERMCRIT_ITER, 30, 0.001);

 

           //进一步提取亚像素角点

           cornerSubPix(img_gray, img_corner_points, Size(11, 11),

               Size(-1, -1), criteria);

 

           //绘制角点

           drawChessboardCorners(image, Size(BOARDSIZE[0], BOARDSIZE[1]), img_corner_points,

               found_success);

 

           objpoints_img.push_back(obj_world_pts);//从世界坐标系到相机坐标系

           images_points.push_back(img_corner_points);

        }

        //char *output = "image";

        char text[] = "image";

        char *output = text;

        imshow(output, image);

        waitKey(200);

 

    }

 

    /*

    计算内参和畸变系数等

    */

 

    Mat cameraMatrix, distCoeffs, R, T;//内参矩阵，畸变系数，旋转量，偏移量

    calibrateCamera(objpoints_img, images_points, img_gray.size(),

        cameraMatrix, distCoeffs, R, T);

 

    cout << "cameraMatrix:" << endl;

    cout << cameraMatrix << endl;

 

    cout << "*****************************" << endl;

    cout << "distCoeffs:" << endl;

    cout << distCoeffs << endl;

    cout << "*****************************" << endl;

 

    cout << "Rotation vector:" << endl;

    cout << R << endl;

 

    cout << "*****************************" << endl;

    cout << "Translation vector:" << endl;

    cout << T << endl;

 

    ///*

    //畸变图像校准

    //*/

    Mat src, dst;

    src = imread("F:/Works/C++/openCV/opencv study/Revise/image/2.jpg");  //F:/Works/C++/openCV/opencv study/Revise/image/2.jpg

    undistort(src, dst, cameraMatrix, distCoeffs);

 

    char texts[] = "image_dst";

    char *dst_output = texts;

    //char *dst_output = "image_dst";

    imshow(dst_output, dst);

    waitKey(100);

    imwrite("F:/Works/C++/openCV/opencv study/Revise/image/3.jpg", dst);

 

    destroyAllWindows();//销毁显示窗口

    system("pause");

    return 0;

}

运行程序，每张图片都会检测角点，如下：

 

最终得到，相机内参及畸变系数：

 

测试畸变前后的图像，以图像2为例：

因此，我们使用的相机自身畸变问题并不突出，所以校正前后图像的变化基本不大。但对于畸变问题突出的相机，一般需要对其进行畸变校正后，方可使用。

 

 标定物的制作精度、摆放位置、现场光照条件等因素都会影响标定结果，同时有些场合不适合放置标定物也限制了静态标定方法的应用。 在售后市场，很多场景下就需要用到动态标定了。

动态标定：主要利用场景约束条件，主要是场景中一些平行（通常需要在有车道线的道路上）或者正交的信息。空间平行线在图像平面上的交点成为消失点，基于消失点的相机自标定算法是最为常见的，其方法灵活性强，可用于动态标定过程。但由于它是基于绝对二次曲线或曲面的方法，鲁棒性会差一些。

 

摄像头内外参标定原理与方法

https://mp.weixin.qq.com/s/1zB1humwW7i17rYNQpgkuA

车载摄像头标定通常由内参、外参、畸变系数三类参数来保证摄像头的准确性。

介绍摄像头内外参标定的基本原理和研鼎的内外参标定设备。

摄像头几何标定主要的目的是，通过一种理论数学模型和优化的手段把摄像头拍到的图像信息转换为熟悉的物理坐标系（xyz）,即建立相机投影模型。

以车载摄像头为例进行推导，ADAS（高级驾驶辅助系统）中存在4个坐标系：

 

 

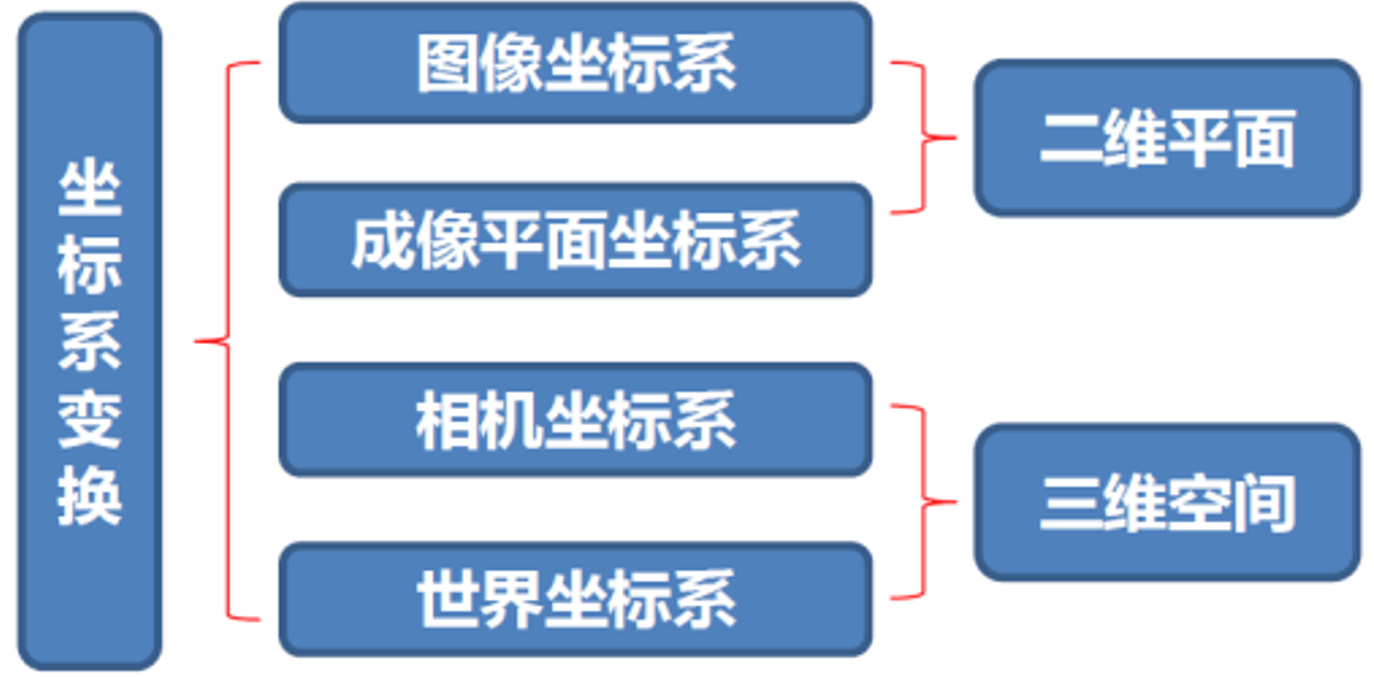
图像坐标系（u, v）

成像平面坐标系（x, y）

相机坐标系（Xc, Yc）

世界坐标系/车辆坐标系（Xw, Yw）

 

 

如上图几何标定是摄像头图像在平面上的(二维空间)点与摄像头所拍摄的现实场景中的(三维空间)点之间关系所需参数的过程。

摄像头几何标定常用的方法是张正友标定法，有感兴趣的朋友可以搜索论文全文（不进行赘述）
研鼎的内外参设备结合了生产线上快速测试所需的运控软件和图像分析标定软件RIQA-Camera，集成了4个高性能摄像头图像采集卡MIG-S2，配合优质的光源1CXL和高平整性棋盘格图卡CP136-R4X，可以针对客户的不同种类的摄像头进行点亮测试设置，并使整个系统可实现摄像头的自动拍图和采图控制及标定。且已经成功地为视场在25°~210°之间的摄像头制定了高兼容性的解决方案，FOV最大可以支持到210°是目前市场上少数能同时标定1~4颗摄像头模组的方案。本方案已经在多个主机厂和摄像头模组厂导入,详细参数规格请参考下图。

 

 自动化程控内参标定设备系统 RT-GVS-F4