图形内存，可编程逻辑阵列，计算分析

图形内存，可编程逻辑阵列，计算分析

内存

1 静态内存（SRAM）

SRAM是指静态随机存取存储器，基本SRAM单元包含两个交叉耦合的反相器，如下图所示。相比之下，基本SR触发器或D触发器包含交叉耦合的NAND门。设计如下所示。

 

SRAM单元的核心包含4个晶体管（每个反相器中有2个），这种交叉耦合布置足以节省单个比特（0或1）。然而，需要一些额外的电路来读取和写入值。此时，在锁存器中使用交叉耦合反相器到底是不是一个坏主意，它们毕竟需要更少的晶体管。将看到，实现用于读取和写入SRAM单元的电路的开销是非常重要的，开销不足以证明以SRAM单元为核心制作锁存器的合理性。

交叉耦合的反相器连接到每一侧（W1、W2）上的晶体管，W1和W2的栅极连接到被称为字线的相同信号，两个反相器W1和W2中的四个晶体管构成SRAM单元，它总共有六个晶体管。现在，如果字线上的电压低，则W1和W2关断，不可能读取或写入SRAM单元。然而，如果字线上的信号为高，则W1和W2导通，可以访问SRAM单元。

下图显示了一个典型的SRAM阵列，SRAM单元被布置为二维矩阵。一行中的所有SRAM单元共享字线，一列中的所有SRAM单元共享一对位线。要激活某个SRAM单元，必须打开其相关的字线，由解码器完成，获取地址位的子集，并打开适当的字线。一行SRAM单元可能包含100多个SRAM单元，通常，会对32个SRAM单元（在32位机器上）的值感兴趣。在这种情况下，列复用器/解复用器选择属于感兴趣的SRAM单元的位线，使用地址中的位的子集作为列选择位。这种设计方法也称为2.5D存储器组织。

 

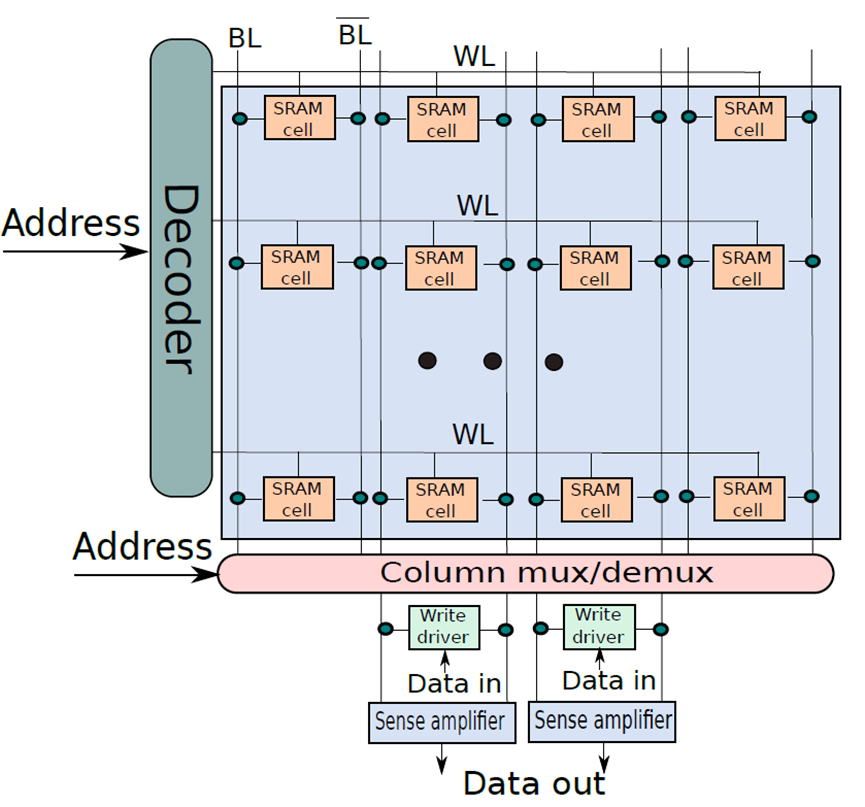
SRAM单元阵列。

2 内容寻址内存（CAM）

下图是10晶体管CAM单元，如果SRAM单元中存储的值V不等于输入位Ai，那么希望将匹配线的值设置为0。在CAM单元中，上半部分是具有6个晶体管的常规SRAM单元，下半部有4个额外的晶体管。现在让考虑晶体管T1，它连接到全局匹配线，晶体管T2。T1由存储在SRAM单元中的值V控制，T2由控制。假设V＝，如果两者都为1，则晶体管T1和T2处于导通状态，并且匹配线和地之间存在直接导电路径。因此，匹配线的值将设置为0。然而，如果V和都为0，则通过T1和T2的路径不导通。但是，在这种情况下，通过T3和T4的路径变得导通，因为这些晶体管的栅极分别连接到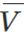和Ai。两个栅极的输入都是逻辑1，因此匹配线将被下拉到0。读取器可以反过来验证，如果V=Ai，则不形成导通路径。因此，如果存储的值与输入位Ai不匹配，则CAM单元将匹配线驱动到逻辑0。

 

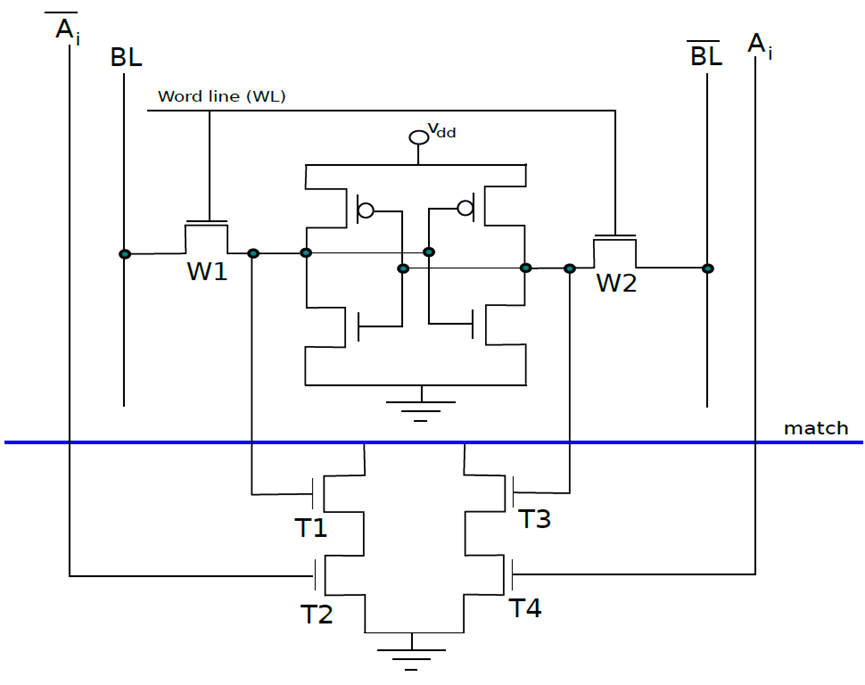
10晶体管CAM单元。

下图显示了CAM单元阵列。该结构主要类似于SRAM阵列。可以通过索引寻址一行，并执行读/写访问，此外可以将CAM单元的每一行与输入A进行比较。如果任何行与输入匹配，则相应的匹配线的值将为1。可以计算所有匹配线的逻辑OR，并确定CAM阵列中是否匹配，此外可以将CAM阵列的所有匹配线连接到优先级编码器，以查找与数据匹配的行的索引。

 

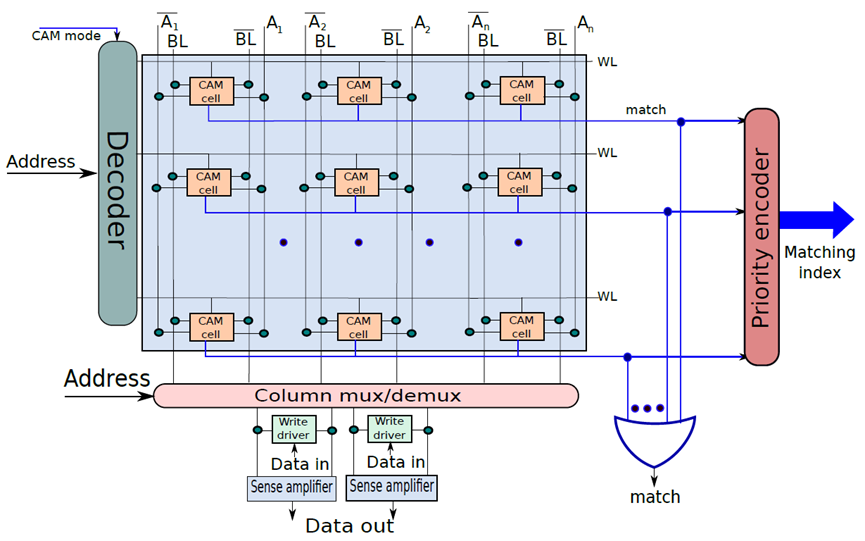
CAM单元阵列。

3 动态内存（DRAM）

现在来看看一种只使用一个晶体管来节省一点时间的存储器技术，它非常密集、面积大，而且能效高，但比SRAM和锁存器慢得多，适用于大型片外存储器。

基本DRAM（动态内存）单元如下图所示。单个晶体管的栅极连接到字线，从而启用或禁用它，其中一个端子连接到存储电荷的电容器。如果存储的位是逻辑1，则电容器带电，否则不带电。

 

一个动态内存的单元。

 

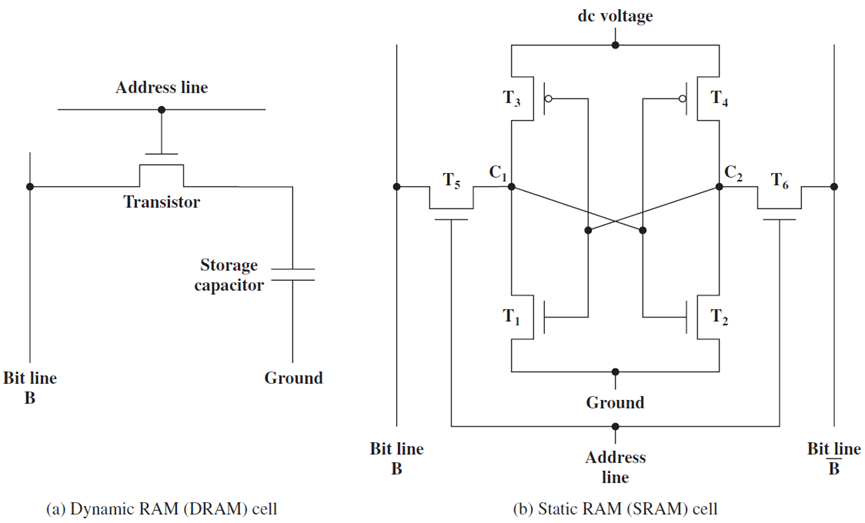
DRAM和SRAM单元的对比图。

因此，读取和写入值非常容易。需要首先设置字线，以便可以访问电容器。为了读取该值，需要感测位线上的电压。如果它处于地电位，则单元存储0，否则如果它接近电源电压，则存储1。类似地，要写入值，需要将位线（BL）设置为适当的电压，并设置字线，电容器将相应地充电或放电。

然而，就DRAM而言，并非一切都是免费的。让假设电容器被充电到等于电源电压的电压，实际上，电容器将通过电介质和晶体管逐渐泄漏一些电荷。该电流很小，但在长时间内电荷的总损失可能很大，最终会使电容器放电。为了防止这种情况，有必要定期刷新DRAM单元的值，亦即需要读取并写回数据值。这也需要在读取操作之后完成，因为电容器在对位线充电时会损失一些电荷。现在让尝试制作一个DRAM单元阵列。

可以用创建SRAM单元阵列的方法构建DRAM单元阵列（下图），有三点不同：

• 存在一条位线而不是两条位线。
• 有一个连接到位线的专用刷新电路。这在读取操作后使用，也会定期调用。
• 在这种情况下，感测放大器出现在列复用器/解复用器之前。读出放大器还为整个DRAM行（也称为DRAM页）缓存数据。它们确保对同一DRAM行的后续访问是快速的，因为它们可以直接从读出放大器进行服务。

 

DRAM单元阵列。

接下来简述现代DRAM的时序方面。在过去的好日子里，DRAM内存是异步访问的，意味着DRAM模块没有做出任何时序保证。但现在每个DRAM操作都与系统时钟同步，因此，如今的DRAM芯片是同步DRAM芯片（SDRAM芯片）。

截至目前，同步DRAM存储器通常使用DDR4或DDR5标准，DDR代表双倍数据速率，使用最早标准DDR1的设备在时钟的上升沿和下降沿向处理器发送8字节的数据包，DDR也被称为双峰（double pump）操作。DDR1的峰值数据速率为1.6 GB/s，后续的DDR世代通过以更高的频率传输数据来扩展DDR1，例如，DDR2的数据速率是DDR1设备的两倍（3.2 GB/s），DDR3通过使用更高的总线频率将峰值传输速率进一步提高了一倍，自2007年开始使用（峰值速率为6.4GB/s）。

4 只读内存（ROM）

只读内存可分为普通ROM和PROM（可编程ROM），下面分别是它们的单元图例。

 

（a） 存储逻辑0的ROM单元；（b） 存储逻辑1的ROM单元。

 

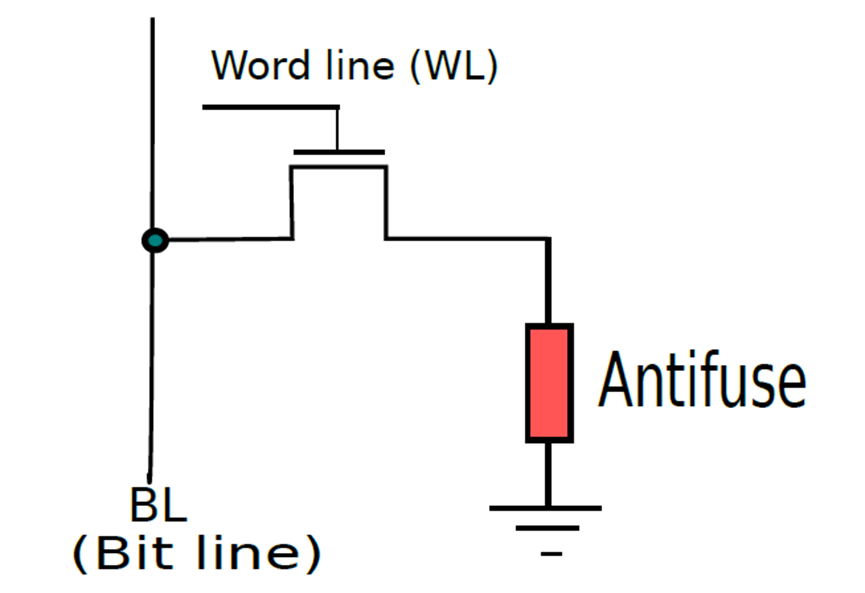
PROM单元。

5 可编程逻辑阵列

事实证明，可以很容易地用类似于PROM单元的存储单元制作组合逻辑电路，这种器件被称为可编程逻辑阵列或PLA。PLA在实践中用于实现由数十或数百个小项（minterm）组成的复杂逻辑函数，相对于由逻辑门组成的硬连线电路的优势在于它是灵活的，可以在运行时更改PLA实现的布尔逻辑，相比之下，由硅制成的电路永远不会改变其逻辑。其次，PLA的设计和编程更简单，而且有很多软件工具可以设计和使用PLA。最后，PLA可以有多个输出，因此可以很容易地实现多个布尔函数。这种额外的灵活性是有代价的，代价是性能。

下图（a）所示的PLA单元原则上类似于基本PROM单元。如果栅极处的值（E）等于1，则NMOS晶体管处于导通状态。因此，NMOS晶体管的源极和漏极端子之间的电压差非常小。换句话说，可以简单地假设结果线的电压等于信号的电压，X. If (E = 0)，NMOS晶体管处于截止状态。结果线是浮动的，并保持其预充电电压。在这种情况下，建议推断逻辑1。

现在让构建一行PLA单元，其中每个PLA单元在其源极端子处连接到输入线，如图（b）所示。输入编号为X1…Xn，所有NMOS晶体管的漏极连接到结果线，PLA单元的晶体管的栅极连接到一组使能信号E1…En。如果任何一个使能信号等于0，则该特定晶体管被禁用，可以将其视为从PLA阵列中逻辑移除。

 

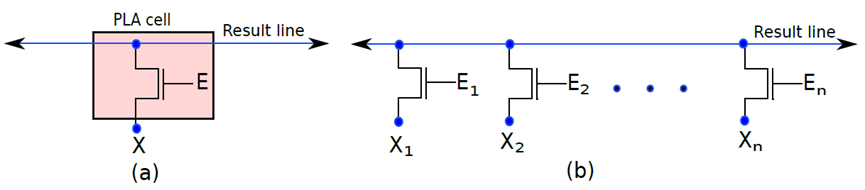
一个PLA单元。

现在让创建一个PLA单元格数组，如下图所示，每行对应一个minterm。对于3变量示例，每行由6列组成，每个变量有2列（原始和补充），例如，前两列分别对应于A和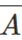。在任何一行中，这两列中只有一列包含PLA单元，因为A和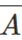不能同时为真。在第一行，计算最小项的值，因此第一行包含对应于的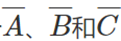列中的PLA单元。在其余行中为剩余的minterm进行类似的连接，PLA阵列的这一部分被称为AND平面，因为正在计算变量值（原始值或补码值）的逻辑AND。PLA阵列的AND平面独立于希望计算的布尔函数，给定输入，它计算所有可能的最小项的值。

 

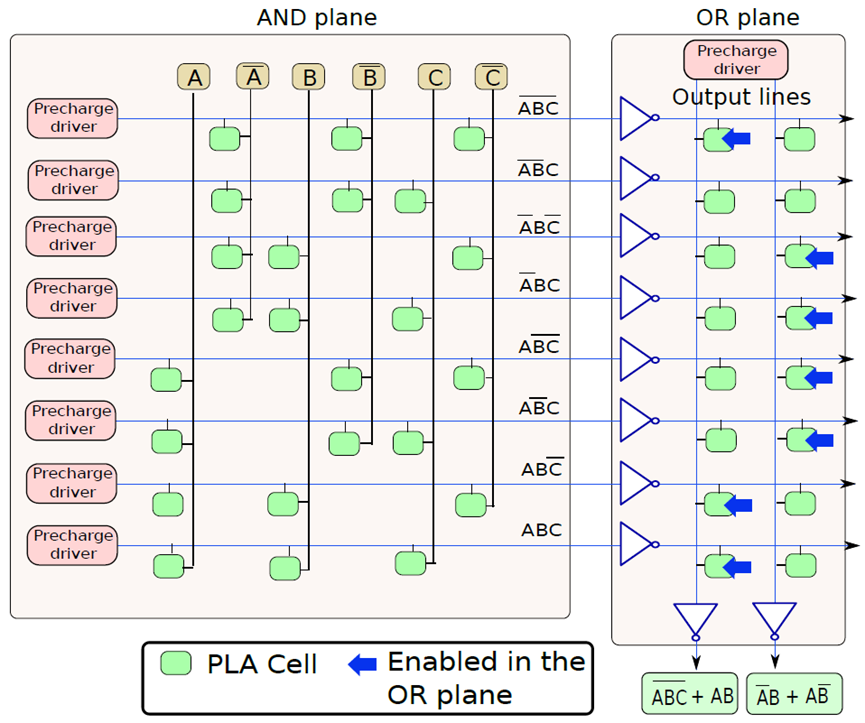
PLA单元阵列。

 

典型的内存封装引脚和信号。

 

256 KB内存组织。

 

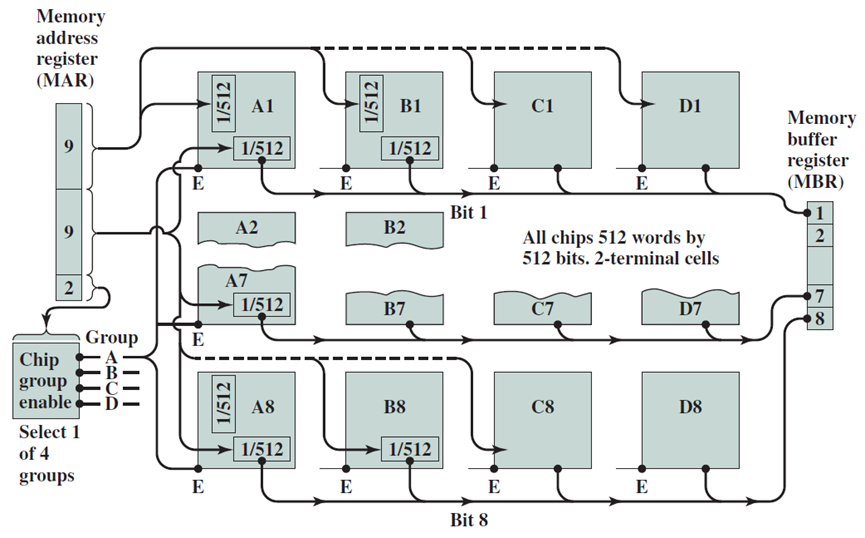
1MB内存组织。

 

DDR代次演进图。

 

非易失性RAM技术。

上：简化的DRAM读取时序；下：Signetics 7489 SRAM的脉冲串。

计算机算术

本节将设计算术运算的硬件算法，先阐整数运算的算法，如两个二进制数相加的基本算法，有很多方法可以完成这些基本操作，每种方法都有自己的优缺点。注意，二进制减法的问题在概念上与2的补码系统中的二进制加法相同。因此，不需要单独对待它。随后，将看到，n个数的相加问题与乘法问题密切相关，而且这是一个硬件上的快速操作。遗憾的是，整数除法并不存在非常有效的方法。然而，将考虑两种用于划分正二进制数的流行算法。

整数算术之后，将研究浮点（带小数点的数字）算术的方法，大多数整数算法稍作修改后都可以移植到浮点数领域。与整数除法相比，浮点除法可以非常有效地完成。

1 加法

让看看将两个1位数字a和b相加的问题，a和b都可以取两个值：0或1，因此，a和b有四种可能的组合，它们的二进制和可以是00、01或10。当a和b均为1时，它们的和将是10，两个1位数字的总和可能有两位长。让将结果的LSB称为和，将MSB称为进位，例如，把8和9相加，和是7，进位是1。

可以将和和进位的概念扩展到加三个1位数字。如果将三个1位数字相加，那么结果的范围是二进制的00到11之间。

和（sum）：总和是两个或三个1位数字相加结果的LSB。
进位（carry）：进位是两个或三个1位数字相加结果的MSB。

对于可以将两个1位数字相加的加法器，将有两个输出位：和s和进位c，将两个位相加的一个加法器称为半加法器（half adder）。半加法的真值表如下表所示。

a	b	s	c
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

 

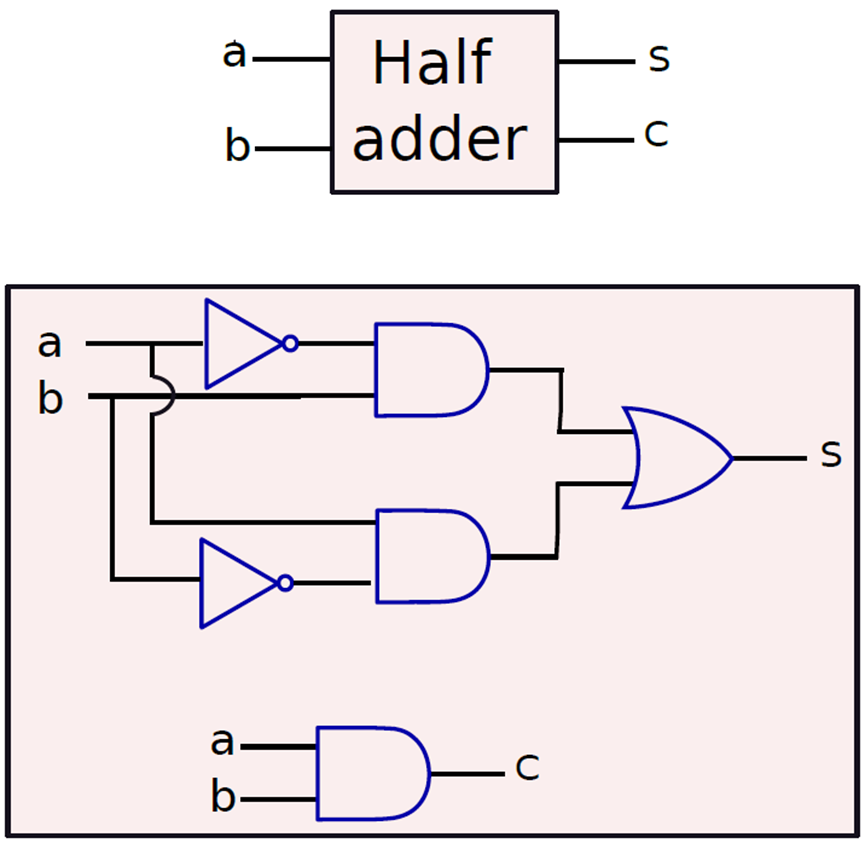
半加法器。

可以加3位的加法器称为全加法器（full adder），它的电子构造如下：

 

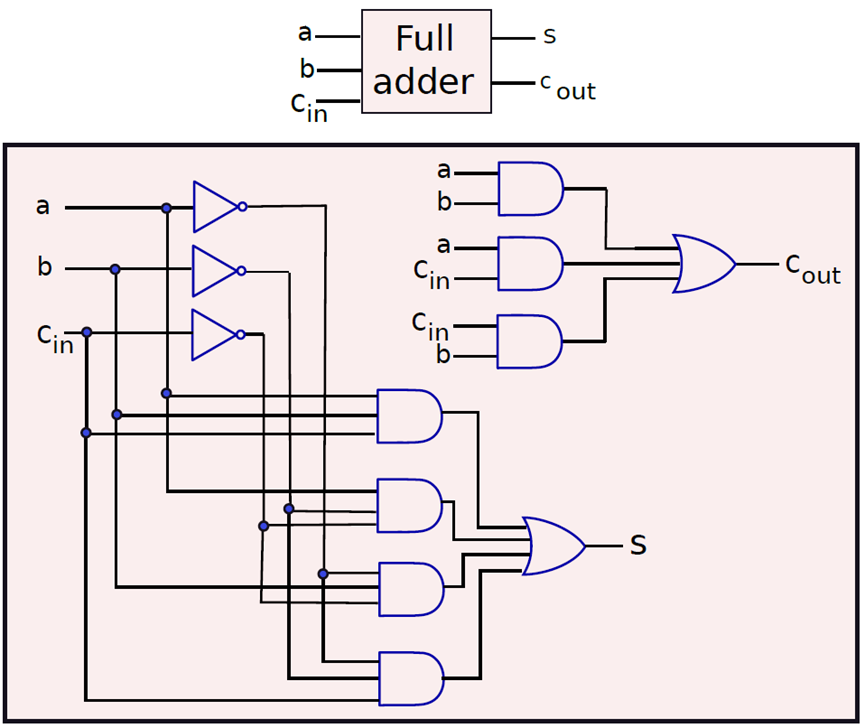
n位加法器被称为纹波进位加法器（ripple carry adder），其设计如下所示：

 

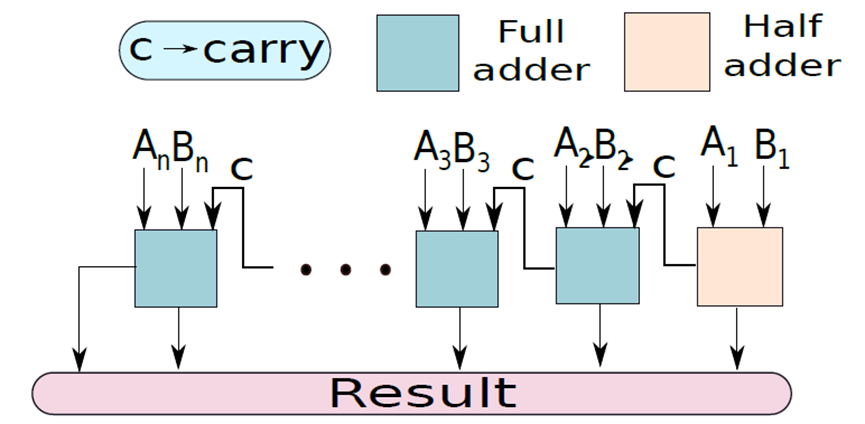
考虑将两个数字A和B相加的问题，首先将比特集划分为4比特的块，如下图所示，每个块包含一个a片段和一个B片段。通过考虑块的输入进位将这两个片段相加，并生成一组和位和一个进位，此进位是后续块的输入进位。

 

此外，还有超前进位加法器（Carry Lookahead Adder），其分为两个阶段，每个阶段都拥有复杂的电子构造。

2 乘法

现与加法类似，先看看两个十进制数相乘的最简单的方法，不妨尝试将13乘以9。在这种情况下，13被称为被乘数（multiplicand），9被称为乘数（multiplier），117是乘积（product）。

下图（a）显示了十进制的乘法，（b）显示了二进制的乘法。请注意，两个二进制数相乘的方法与十进制数完全相同。需要考虑乘数从最小显著位置到最大显著位置的每一位。如果该位为1，那么将被乘数的值写在该行下方，否则将写0。对于每个乘数位，将被乘数向左移动一位。其原因是每个乘数位代表2的更高幂。将每个这样的值称为部分和（见图7.10（b））。如果乘法器有m位，那么需要将m个部分和相加以获得乘积。在这种情况下，乘积是十进制117，二进制1110101。读者可以验证它们实际上表示相同的数字。为了便于以后的表示，让定义另一个称为部分积的术语。它是部分和的连续序列的和。

 

（a）十进制乘法；（b）二进制乘法。

常规的乘法器是，而改进版的Booth乘法器或Wallace树形乘法器（下图）可以做到的算法复杂度。

 

Wallace树形乘数。

3 除法

现在让看看整数除法。不幸的是，与加法、减法和乘法不同，除法是一个明显较慢的过程。任何除法运算都可以表示如下：

N=DQ+R

N是被除数，D是除数，Q是商，R是余数。假定除数和被除数为正，除法过程需要满足以下属性：

• R<D且R≥0。
• Q是满足上述等式的最大正整数。

如果想除掉负数，那么首先将它们转换成正数，进行除法，然后调整商和余数的符号，部分ISA试图确保余数始终为正。在这种情况下，需要将商减1，并将除数与余数相加，使其为正。

实现除法的方式有迭代除法、佘数恢复除法（Restoring Division）、非余数恢复除法（Non-Restoring Division）等。本文忽略这些算法的具体描述，有兴趣的童鞋可以自行查阅资料。

4 浮点数运算

浮点加法和减法的问题实际上是同一问题的不同方面。A-B可以用两种方式解释，可以说正在从A中减去B，也可以说在将-B加到A中。因此，与其单独看减法，不如将其视为加法的特例。浮点数的二进制表示、属性和特殊含义可以参见浮点数。

下图显示了一个示例，说明了如何将有效位解压缩，并将其放入普通浮点数的寄存器中。在32位IEEE 754格式中，尾数有23位，小数点前有0或1。因此，有效位需要24位，如果希望添加前导符号位（0），那么需要25位存储。让把这个号码保存在一个寄存器中，并称之为W。

 

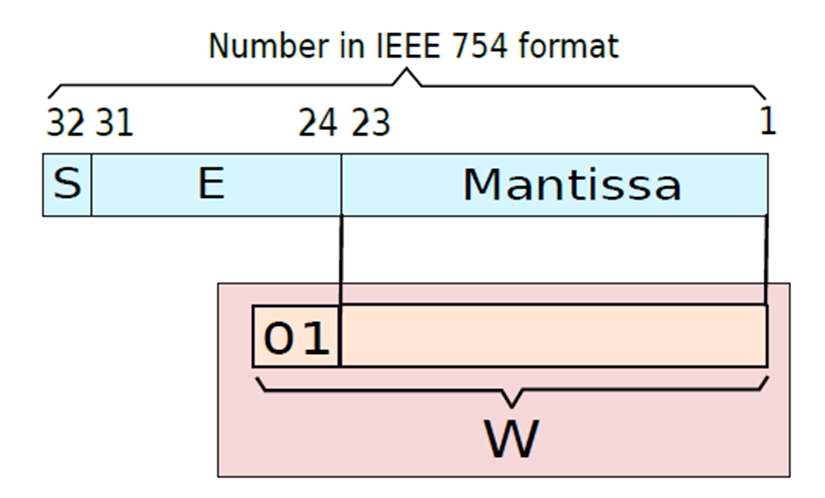
展开有效位并放入寄存器。

 

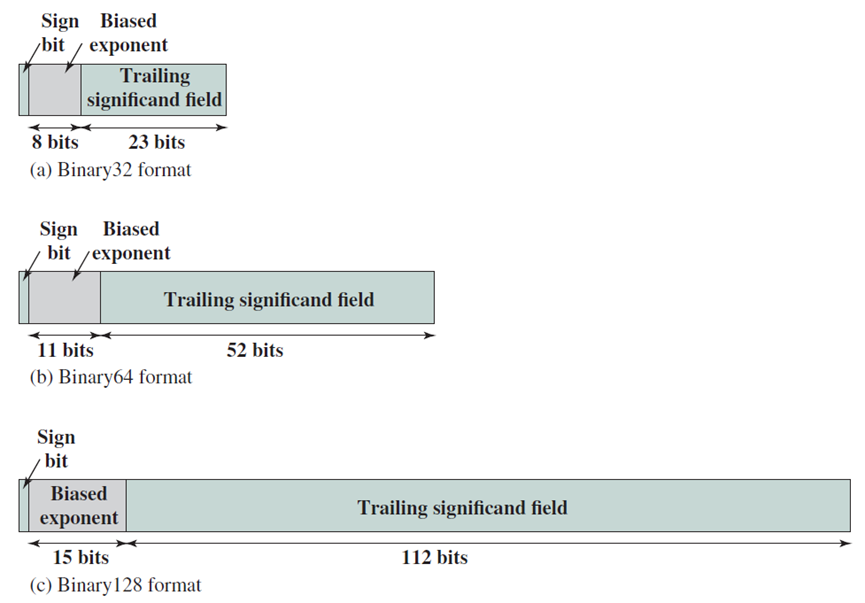
IEEE 754格式。

浮点数的运算涉及舍入等考量，下图显示了两个浮点数相加的算法，考虑了0值。

 

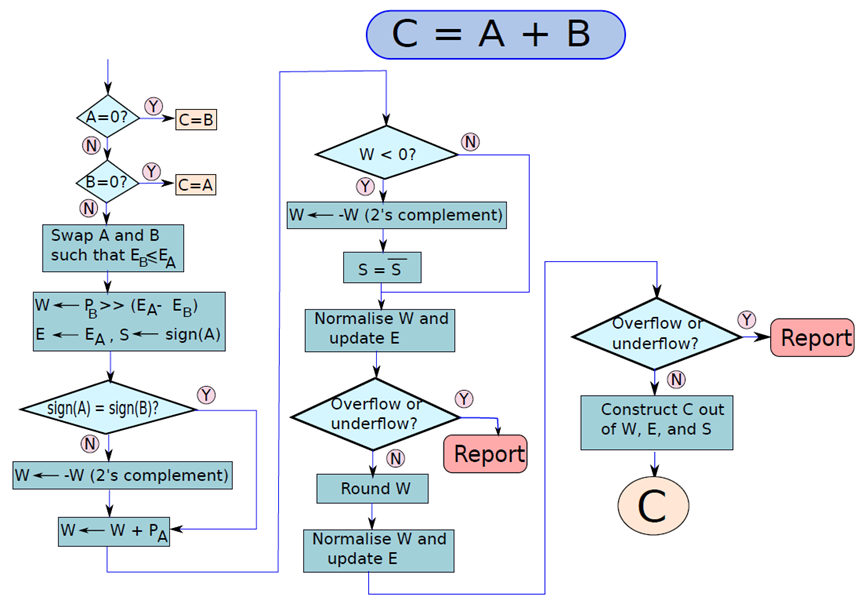
累加两个浮点值的流程图。

浮点数相乘算法与泛型加法算法的形式完全相同，只需几步。让尝试乘以A x B以获得乘积C，乘法的流程图如下图所示。在乘法的情况下，不必对齐指数，如下初始化算法，将B的符号和装入寄存器W，W的宽度等于操作数大小的两倍，就可以容纳乘积。E寄存器初始化为EA+EB−bias，因为在乘法的情况下，指数相加，减去bias以避免重复计数，计算结果的符号很简单。

 

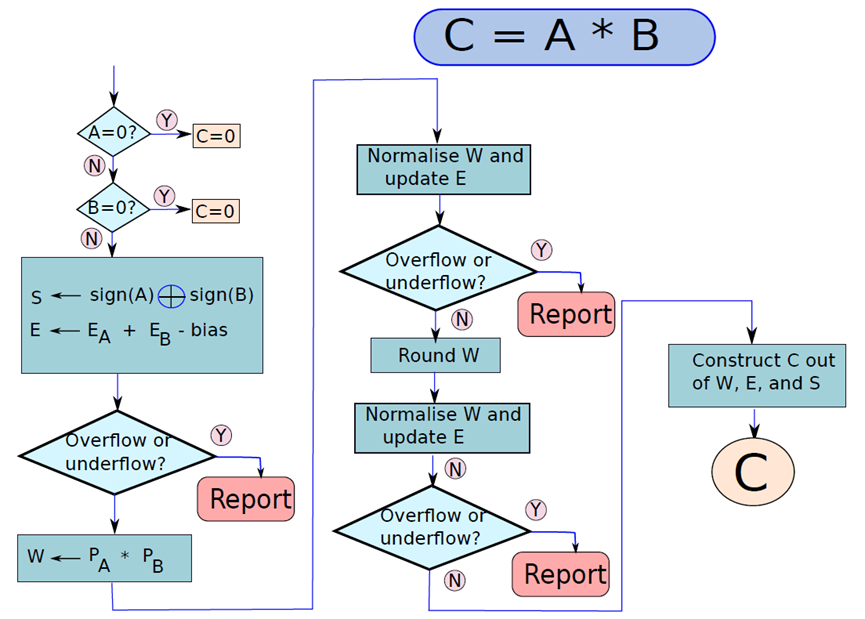
两个浮点值相乘的流程图。

此外，还有Goldschmidt除法以及Newton-Raphson除法。

 

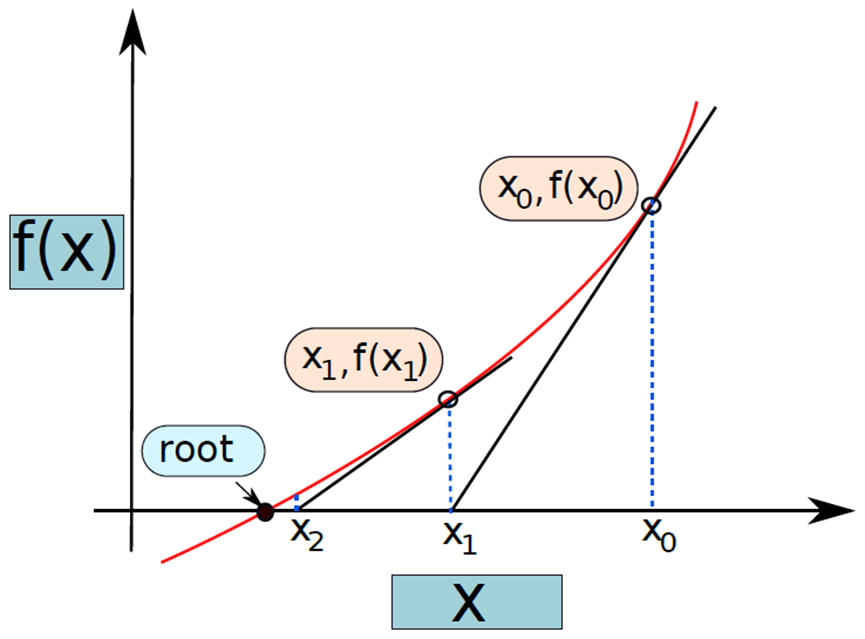
Newton-Raphson方法。