LOFAR & DEMON 频谱分析

LOFAR & DEMON 频谱分析

LOFAR (Low frequency analysis and recording)谱可反映信号的非平稳特性，进而可提取信号中的宽带线谱分布特征。但是轴频及其倍频却因为基本上都淹没在低频宽带噪声中而无法直接获取。

而舰船宽带噪声高频段存在调制现象，DEMON (Detection of Envelope Modulation On Noise)分析通过对接收的宽带信号进行解调以获得低频的包络谱，从而获得了诸如目标轴频、叶频等低频段较强的物理特征。

可以说，由LOFAR分析可获得反应舰船目标各部件结构特征的宽频带特征，而DEMON分析则获得较低频段的强制线谱特征，弥补了LOFAR分析在低频段的不足，共同描绘了目标信号的谱系特征。

LOFAR谱图分析

LOFAR谱图分析是较具代表性的被动声纳信号处理方法之一。该方法通过对采样数据作短时傅立叶变换而构成信号表达的三维图（声谱图）。

当噪声信号随时间发生比较明显的变化，即信号出现非平稳特性时，建立在平稳性假设基础上的传统的傅立叶表示方法已不适合应用。而信号的LOFAR谱图从时间和频率两个角度对信号进行联合域分析，适宜于水声目标辐射噪声的局部平稳特性。

LOFAR谱图的具体实现步骤如下：
（1）将原始信号的采样序列分成连续的若干段，每段N个采样点。根据具体情况，段间可有部分重叠。
（2）对每段信号采样样本L(n)" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-1-Frame">L(n)作归一化和中心化处理，归一化处理的目的是使接收信号的幅度（或方差）在时间上均匀；中心化是为了使样本的均值为零。

 (3)对信号x(n)" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-4-Frame">x(n)作短时傅立叶变换得到LOFAR谱图。

 DEMON谱图分析

DEMON谱是从接收信号的高频调制谱中解调出的线谱信息，是一种常用的获取轴频与倍频的方法。

在舰船辐射噪声中，螺旋桨节拍对舰船的辐射噪声存在着明显的振幅调制，调制频率等于螺旋桨转速或螺旋桨叶片频率（轴频乘以叶片数目）。因此舰船辐射噪声具有鲜明的节奏感。这种幅度调制信号即包络信号是一种慢变化信号，它反映了能量随时间的变化，由周期性成分和非周期性成分组成。通常采用宽带噪声包络调制分析技术测量其基频和各次谐波，提取螺旋桨的轴频和叶片频，这种方法称为DEMON。

在DEMON分析中，一般选取调制最强的时变谱频段进行包络检测，然后进行频谱分析得到DEMON谱。根据信号调制的原理，舰船噪声以周期性局部平稳过程为模型可表示为：

n(t)是宽带平稳白色高斯随机过程；

f(t)" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-7-Frame">f(t)是调制函数，它是慢变化的周期函数，它所在的频域比n(t)" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-8-Frame">n(t)所在频域的频率要低得多。
利用平方解调方法即可获得调制信号f(t)" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-9-Frame">f(t)。
再对获得的解调信号进行FFT处理即可得到解调信号的DEMON谱。
这可以称为基本的DEMON分析过程，流程图：-->带通滤波-->平方检波-->低通滤波-->FFT

仅仅做基本的DEMON分析是不够的，不能获得理想的DEMON线谱。舰船噪声调制信号对不同频带噪声信号的调制程度不一样，对某些频带调制强，对其它频带则相对调制弱些。另外，各个频带的DEMON谱线也不可能完全相同，不同频段存在不同的谱线缺失现象，同时还可能存在“虚假谱线”。采用分频段处理结果的方法可以弥补单一频段解调DEMON谱处理的不足。
由于所获得的DEMON谱中存在连续谱而使线谱成分不明显，还存在谱线靠的太近而无法分辨的情况，使DEMON谱看起来比较“模糊”。这就要求将分频段处理再融合获得的DEMON谱中的连续谱去除，并进一步进行线谱净化处理，使谱线更加清晰。

 应用α" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-10-Frame">α双向滤波器获得DEMON谱的趋势项，再以趋势项适当的倍数为门限，保留原始DEMON谱中过此门限的谱线即可做到线谱与连续谱的分离，获得DEMON谱线。

α" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-11-Frame">α双向滤波器是一阶递归滤波器，设某采样信号s(n)" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-12-Frame">s(n)长度为N" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-13-Frame">N，当n=1,2,...,N−1" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-14-Frame">n=1,2,...,N−1、m=1,2,...,N" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-15-Frame">m=1,2,...,N时，α" role="presentation" style="display:inline-block;overflow-wrap: normal;max-width: none; max-height: none;min-width: 0px;min-height: 0px;float:none;word-spacing:normal" id="MathJax-Element-16-Frame">α双向滤波器的基本原理可表示为

sm(k)为经过α双向滤波器后获得的信号，Q为递归系数，递归系数的值越大，跟踪能力越好，滤波效果越差。当递归系数取2的整数幂的形式时，用移位就可以实现整个滤波，并且不用担心溢出问题。

综上所述，将DEMON分析方法的具体实现步骤归纳整理如下：
（1）选取可能具有较强振幅调制的目标噪声信号的频带，一般选择大于1000Hz某频带范围（例如3000-5000Hz）的信号，将此频带内的信号按照一定的规律（平均或按比例或按频程）分为N个频带进行时域滤波，对每个频带的信号分别进行平方检波以得到其包络信号，对包络信号进行FFT运算获得到该频带的DEMON谱，假设为Pi,i=1,2,...,N。
（2）对每个频带的解调信号的DEMON谱Pi进行加权处理。将第i(1≤i≤N)个频段的DEMON谱Pi经过α双向滤波器，适当选取递归系数Q的值，可得到趋势项即连续谱Pi。
（3）将以上获得的N个归一化处理的DEMON线谱和与其相应的加权系数相乘，再进行求和就得到了较完善的DEMON谱P。
（4）DEMON线谱P的净化。经过α双向滤波器，适当选取递归系数Q的值，得到趋势项即连续谱P。...
基本频谱分析示例

傅里叶变换是用于对时域信号执行频率和功率谱分析的工具。

频谱分析数量

频谱分析研究非均匀采样的离散数据中包含的频谱。傅里叶变换是通过在频率空间表示基于时间或空间的信号来揭示该信号的频率分量的工具。下表列出了用于描述和解释信号属性的常用量。

含噪信号

尝试此示例Copy Code  Copy Command

傅里叶变换可以计算被随机噪声破坏的信号的频率分量。

创建具有 15 Hz 和 40 Hz 分量频率的信号，并插入随机高斯噪声。

rng('default')

fs = 100;                                % sample frequency (Hz)

t = 0:1/fs:10-1/fs;                      % 10 second span time vector

x = (1.3)*sin(2*pi*15*t) ...             % 15 Hz component

  + (1.7)*sin(2*pi*40*(t-2)) ...         % 40 Hz component

  + 2.5*randn(size(t));                  % Gaussian noise;

信号的傅里叶变换可确定其频率分量。在 MATLAB® 中，fft 函数使用快速傅里叶变换算法计算傅里叶变换。使用 fft 计算信号的离散傅里叶变换。

y = fft(x);

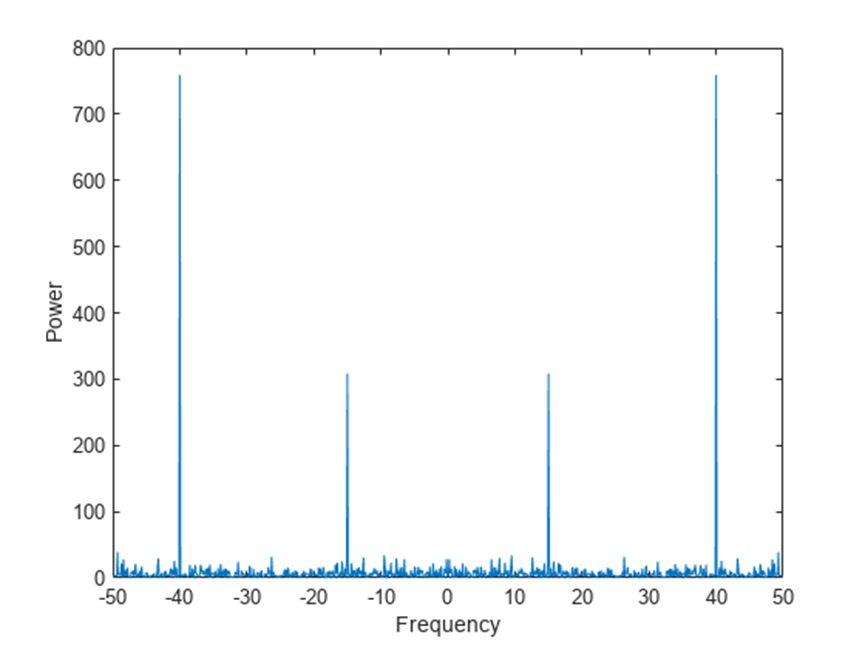
将功率谱绘制为频率的函数。尽管噪声在基于时间的空间内伪装成信号的频率分量，但傅里叶变换将其显现为功率尖峰。

n = length(x);          % number of samples

f = (0:n-1)*(fs/n);     % frequency range

power = abs(y).^2/n;    % power of the DFT

 

plot(f,power)

xlabel('Frequency')

ylabel('Power')

 在许多应用中，查看以 0 频率为中心的功率谱更加方便，因为它能更好地显示信号的周期性。使用 fftshift 函数对 y 执行循环平移，并绘制以 0 为中心的功率。

y0 = fftshift(y);         % shift y values

f0 = (-n/2:n/2-1)*(fs/n); % 0-centered frequency range

power0 = abs(y0).^2/n;    % 0-centered power

 

plot(f0,power0)

xlabel('Frequency')

ylabel('Power')

 音频信号

您可以使用傅里叶变换来分析音频数据的频谱。

文件 bluewhale.au 包含水下麦克风记录的加利福尼亚海岸的太平洋蓝鲸发声的音频数据。此文件来自于康奈尔大学生物声学研究项目保存的动物发声库。

由于蓝鲸的叫声频率如此之低，以至人类几乎听不到。数据中的时间标度压缩了 10 倍，以便提高音调并使叫声更清晰可闻。读取并绘制音频数据。可使用命令 sound(x,fs) 来收听音频。

whaleFile = 'bluewhale.au';

[x,fs] = audioread(whaleFile);

 

plot(x)

xlabel('Sample Number')

ylabel('Amplitude')

 第一个声音为“颤音”，之后是三个“呻吟音”。本示例将分析单个呻吟音。指定大致包含第一个呻吟音的新数据，并校正时间数据以体现 10 部的加速。将截断的信号绘制为时间的函数。

moan = x(2.45e4:3.10e4);

t = 10*(0:1/fs:(length(moan)-1)/fs);

 

plot(t,moan)

xlabel('Time (seconds)')

ylabel('Amplitude')

xlim([0 t(end)])

 数据的傅里叶变换确定了音频信号的频率分量。在一些使用 fft 处理大量数据的应用中，通常需要调整输入，使样本数量为 2 的幂。这样可以大幅提高变换计算的速度，对于具有较大质因数的样本大小更是如此。指定新的信号长度 n（2 的幂），并使用 fft 函数计算信号的离散傅里叶变换。fft 会自动使用零来填充原始数据，以增加样本大小。

m = length(moan);       % original sample length

n = pow2(nextpow2(m));  % transform length

y = fft(moan,n);        % DFT of signal

根据加速因子调整频率范围，并计算和绘制信号的功率谱。绘图指示，呻吟音包含约 17 Hz 的基本频率和一系列谐波（其中强调了第二个谐波）。

f = (0:n-1)*(fs/n)/10;

power = abs(y).^2/n;     

 

plot(f(1:floor(n/2)),power(1:floor(n/2)))

xlabel('Frequency')

ylabel('Power')