机器学习语音处理：滤波器组、梅尔频率倒谱系数 （MFCC）

机器学习语音处理：滤波器组、梅尔频率倒谱系数 （MFCC） 以及介于两者之间的内容

语音处理在任何语音系统中都起着重要作用，无论是自动语音识别（ASR）还是说话人识别或其他东西。长期以来，梅尔频率倒谱系数 （MFCC） 是非常流行的特征;但最近，过滤器库变得越来越受欢迎。本文将讨论过滤器组和MFCC，以及为什么过滤器组越来越受欢迎。

计算滤波器组和 MFCC 涉及大致相同的过程，在这两种情况下，都会计算滤波器组，并且可以通过更多额外的步骤获得 MFCC。简而言之，信号通过预加重滤波器;然后被切成（重叠）帧，并将窗口函数应用于每个帧;之后，对每一帧进行傅里叶变换（或者更具体地说是短时傅里叶变换）并计算功率谱；并随后计算过滤器组。为了获得MFCC，将离散余弦变换（DCT）应用于滤波器组，保留许多结果系数，而其余系数则被丢弃。这两种情况下的最后一步都是均值归一化。

设置

在这篇文章中，使用了一个 16 位 PCM wav 文件，称为“OSR_us_000_0010_8k.wav”，其采样频率为 8000 Hz。wav 文件是一个干净的语音信号，由一个声音组成，说出一些句子，中间有一些停顿。为简单起见，使用了信号的前 3.5 秒，它大致对应于 wav 文件中的第一句话。

将使用Python 2.7.x，NumPy和SciPy。本文使用的一些代码基于存储库中可用的代码。

import scipy.io.wavfile
from scipy.fftpack import dct

sample_rate, signal = scipy.io.wavfile.read('OSR_us_000_0010_8k.wav') # File assumed to be in the same directory
signal = signal[0:int(3.5 * sample_rate)] # Keep the first 3.5 seconds

原始信号在时域中具有以下形式：

时域信号

预加重

第一步是在信号上应用预加重滤波器以放大高频。预加重滤波器在以下几个方面很有用：（1）平衡频谱，因为高频通常比低频具有较小的幅度，（2）避免傅里叶变换操作期间的数值问题，以及（3）还可以提高信噪比（SNR）。

预加重滤波器可应用于信号x在以下等式中使用一阶滤波器：

 可以使用以下行轻松实现，其中滤波器系数的典型值（α" role="presentation" id="MathJax-Element-3-Frame">α）为 0.95 或0.97, pre_emphasis = 0.97:

emphasized_signal = numpy.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])

预加重在现代系统中具有适度的影响，主要是因为预加重滤波器的大多数动机都可以使用均值归一化（本文后面讨论）来实现，除了避免傅里叶变换数值问题，这在现代FFT实现中应该不是问题。

预加重后的信号在时域中具有以下形式：

预加重后时域中的信号

框架

在预加重之后，需要将信号分成短时间框架。此步骤背后的基本原理是信号中的频率随时间变化，因此在大多数情况下，在整个信号上进行傅里叶变换是没有意义的，因为会随着时间的推移失去信号的频率轮廓。为了避免这种情况，可以安全地假设信号中的频率在很短的时间内是静止的。因此，通过在这个短时间内进行傅里叶变换，可以通过连接相邻帧来获得信号频率轮廓的良好近似值。

语音处理中的典型帧大小范围为 20 毫秒到 40 毫秒，连续帧之间有 50% （+/-10%） 重叠。

常用设置为帧大小为 25 毫秒，frame_size = 0.025，步幅为 10 毫秒（重叠 15 毫秒），frame_stride = 0.01。

frame_length, frame_step = frame_size * sample_rate, frame_stride * sample_rate # Convert from seconds to samples
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
num_frames = int(numpy.ceil(float(numpy.abs(signal_length - frame_length)) / frame_step)) # Make sure that we have at least 1 frame

pad_signal_length = num_frames * frame_step + frame_length
z = numpy.zeros((pad_signal_length - signal_length))
pad_signal = numpy.append(emphasized_signal, z) # Pad Signal to make sure that all frames have equal number of samples without truncating any samples from the original signal
indices = numpy.tile(numpy.arange(0, frame_length), (num_frames, 1)) + numpy.tile(numpy.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(numpy.int32, copy=False)]

窗

将信号切成帧后，将汉明窗口等窗口函数应用于每个帧。汉明窗口具有以下形式：

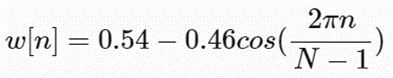
其中0≤n≤N−1, N是窗口长度。绘制上一个等式将生成以下图：

汉明窗

需要对帧应用窗口函数有几个原因，特别是为了抵消FFT所做的数据是无限的假设并减少频谱泄漏。

frames *= numpy.hamming(frame_length)
# frames *= 0.54 - 0.46 * numpy.cos((2 * numpy.pi * n) / (frame_length - 1)) # Explicit Implementation **

傅里叶变换和功率谱

 

现在可以做一个N" role="presentation" id="MathJax-Element-7-Frame">N-点FFT在每个帧上计算频谱，也称为短时傅里叶变换（STFT），其中N" role="presentation" id="MathJax-Element-8-Frame">N通常为 256 或 512， ;然后使用以下公式计算功率谱（周期图）：NFFT = 512

Xi是第 i个x信号帧。这可以通过以下行实现：

mag_frames = numpy.absolute(numpy.fft.rfft(frames, NFFT)) # Magnitude of the FFT
pow_frames = ((1.0 / NFFT) * ((mag_frames) ** 2)) # Power Spectrum

过滤器组

 计算滤波器组的最后一步是在功率谱上应用三角滤波器（通常为 40 个滤波器）以 Mel 级提取频段。Mel 量表旨在模仿人耳对声音的非线性感知，在较低频率下更具辨别力，在较高频率下具有较少的辨别力。可以在赫兹 可以在赫兹 Hertz (f) 和Mel (m) 和梅尔（m）使用以下等式：

滤波器组中的每个滤波器都是三角形的，在中心频率处的响应为1，并线性下降到0，直到达到响应为0的两个相邻滤波器的中心频率，如下图所示：

Mel-Scale 上的过滤器组

这可以通过以下等式进行建模：

low_freq_mel = 0
high_freq_mel = (2595 * numpy.log10(1 + (sample_rate / 2) / 700)) # Convert Hz to Mel
mel_points = numpy.linspace(low_freq_mel, high_freq_mel, nfilt + 2) # Equally spaced in Mel scale
hz_points = (700 * (10**(mel_points / 2595) - 1)) # Convert Mel to Hz
bin = numpy.floor((NFFT + 1) * hz_points / sample_rate)

fbank = numpy.zeros((nfilt, int(numpy.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
f_m_minus = int(bin[m - 1]) # left
f_m = int(bin[m]) # center
f_m_plus = int(bin[m + 1]) # right

for k in range(f_m_minus, f_m):
fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
for k in range(f_m, f_m_plus):
fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])
filter_banks = numpy.dot(pow_frames, fbank.T)
filter_banks = numpy.where(filter_banks == 0, numpy.finfo(float).eps, filter_banks) # Numerical Stability
filter_banks = 20 * numpy.log10(filter_banks) # dB

将滤波器组应用于信号的功率谱（周期图）后，得到以下频谱图：

信号频谱图

如果 Mel 缩放过滤器组是所需的特征，那么可以跳过平均归一化。

梅尔频率倒谱系数

事实证明，在上一步中计算的滤波器组系数是高度相关的，这在某些机器学习算法中可能存在问题。因此，可以应用离散余弦变换（DCT）来解关联滤波器组系数，并生成滤波器组的压缩表示。通常，对于自动语音识别 （ASR），生成的倒谱系数 2-13 被保留，其余的被丢弃，num_ceps = 12; 丢弃其他系数的原因是它们表示滤波器组系数的快速变化，并且这些精细细节对自动语音识别 （ASR） 没有贡献。

mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)] # Keep 2-13

可以将正弦提升¹应用于MFCC以减轻高MFCC，据称可以改善噪声信号中的语音识别。

(nframes, ncoeff) = mfcc.shape
n = numpy.arange(ncoeff)
lift = 1 + (cep_lifter / 2) * numpy.sin(numpy.pi * n / cep_lifter)
mfcc *= lift #*

生成的 MFCC：

MFCCs

均值归一化

如前所述，为了平衡频谱并改善信噪比（SNR），可以简单地从所有帧中减去每个系数的平均值。

filter_banks -= (numpy.mean(filter_banks, axis=0) + 1e-8)

均值归一化滤波器组：

归一化过滤器组

同样，对于MFCC：

mfcc -= (numpy.mean(mfcc, axis=0) + 1e-8)

均值归一化 MFCC：

标准化 MFCC

过滤器组与MFCC

到目前为止，从动机和实现的角度讨论了计算滤波器组和MFCC的步骤。有趣的是，计算滤波器组所需的所有步骤都是由语音信号的性质和人类对此类信号的感知所驱动的。相反，计算 MFCC 所需的额外步骤是由某些机器学习算法的限制引起的。需要离散余弦变换（DCT）来解相关滤波器组系数，这一过程也称为白化。特别是，当高斯混合模型 - 隐马尔可夫模型（GMM-HMM）非常流行时，MFCC非常流行，并且MFCC和GMM-HMM共同演变为自动语音识别（ASR）^的标准方式2。随着深度学习在语音系统中的出现，人们可能会质疑MFCC是否仍然是正确的选择，因为深度神经网络不太容易受到高度相关的输入的影响，因此离散余弦变换（DCT）不再是必要的步骤。值得注意的是，离散余弦变换（DCT）是一种线性变换，因此是不可取的，因为它丢弃了语音信号中的一些高度非线性的信息。

质疑傅里叶变换是否是必要的操作是明智的。鉴于傅里叶变换本身也是一种线性运算，因此忽略它并尝试直接从时域中的信号中学习可能是有益的。事实上，最近的一些工作已经尝试了这一点，并报告了积极的结果。然而，傅里叶变换运算是一个难以学习的操作，并且可能会增加实现相同性能所需的数据量和模型复杂性。此外，在进行短时傅里叶变换（STFT）时，假设信号在短时间内是静止的，因此傅里叶变换的线性度不会构成关键问题。

结论

在这篇文章中，探讨了计算梅尔尺度滤波器组和梅尔频率倒谱系数 （MFCC） 的过程。讨论了程序中每个步骤的动机和实施。还讨论了与MFCC相比，过滤器组越来越受欢迎的原因。

如果机器学习算法不容易受到高度相关输入的影响，请使用 Mel 缩放的筛选器组。如果机器学习算法容易受到相关输入的影响，请使用 MFCC。