卷积与矩阵相乘编译部署分析
卷积与矩阵相乘编译部署分析
深度学习中的各种卷积
如果你听过深度学习中不同的卷积类型,包括:
2D, 3D, 1*1, Transposed, Dilated, Spatially Separable, Depthwise Separable, Flattened, Grouped, Shuffled Grouped Convolution, ...这些,但是并不清楚它们实际意味着什么,本文就是带大家学习这些卷积到底是如何工作的。在本文中,我尽量使用简单明了的方式向大家解释深度学习中常用的几种卷积,希望能够帮助你建立学习体系,并为你的研究提供参考。1. Convolution VS Cross-correlation
卷积是一项在信号处理、视觉处理或者其他工程/科学领域中应用广泛的技术。在深度学习中,有一种模型架构,叫做Convolution Neural Network。深度学习中的卷积本质上就是信号处理中的Cross-correlation。当然,两者之间也存在细微的差别。
在信号/图像处理中,卷积定义如下:
由上公式可以看出,卷积是通过两个函数f和g生成第三个函数的一种数学算子。对f与经过翻转和平移的g乘积进行积分。过程如下:

信号处理中的卷积。滤波器g首先翻转,然后沿着横坐标移动。计算两者相交的面积,就是卷积值。另一方面,Cross-correlation被称为滑动点积或者两个函数的滑动内积。Cross-correlation中的滤波器函数是不用翻转的。它直接划过特征函数f。f和g相交的区域就是Cross-correlation。

在深度学习中,卷积中的滤波器不翻转。严格来说,它是Cross-correlation。我们基本上执行元素对元素的加法或者乘法。但是,在深度学习中,我们还是习惯叫做Convolution。滤波器的权重是在训练期间学习的。
2. Convolution in Deep Learning
卷积的目的是为了从输入中提取有用的特征。在图像处理中,有很多滤波器可以供我们选择。每一种滤波器帮助我们提取不同的特征。比如水平/垂直/对角线边缘等等。在CNN中,通过卷积提取不同的特征,滤波器的权重在训练期间自动学习。然后将所有提取到的特征“组合”以作出决定。
卷积的优势在于,权重共享和平移不变性。同时还考虑到了像素空间的关系,而这一点很有用,特别是在计算机视觉任务中,因为这些任务通常涉及识别具有空间关系的对象。(例如:狗的身体通常连接头部、四肢和尾部)。The single channel version
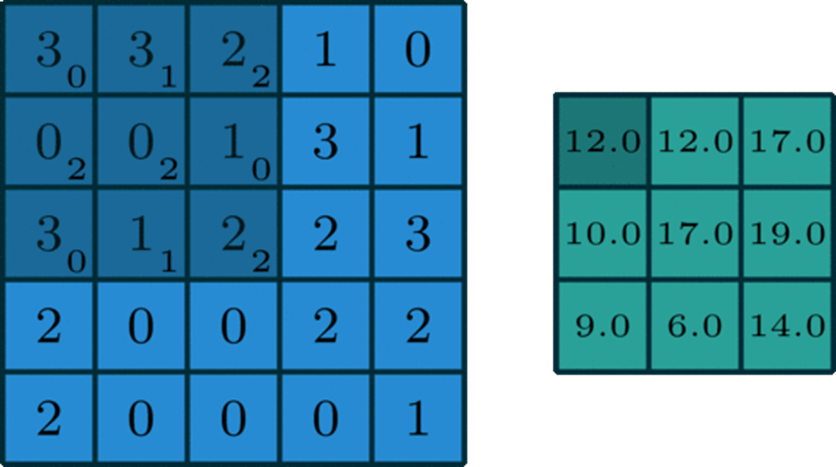
单个通道的卷积
在深度学习中,卷积是元素对元素的加法和乘法。对于具有一个通道的图像,卷积如上图所示。在这里的滤波器是一个3x3的矩阵[[0,1,2],[2,2,0],[0,1,2]]。滤波器滑过输入,在每个位置完成一次卷积,每个滑动位置得到一个数字。最终输出仍然是一个3x3的矩阵。(注意,在上面的例子中,stride=1,padding=0)The muti-channel version
在很多应用中,我们需要处理多通道图片。最典型的例子就是RGB图像。

不同的通道强调原始图像的不同方面另一个多通道数据的例子是CNN中的层。卷积网络层通常由多个通道组成(通常为数百个通道)。每个通道描述前一层的不同方面。我们如何在不同深度的层之间进行转换?如何将深度为n的层转换为深度为m下一层?在描述这个过程之前,我们先介绍一些术语:layers(层)、channels(通道)、feature maps(特征图),filters(滤波器),kernels(卷积核)。从层次结构的角度来看,层和滤波器的概念处于同一水平,而通道和卷积核在下一级结构中。通道和特征图是同一个事情。一层可以有多个通道(或者说特征图)。如果输入的是一个RGB图像,那么就会有3个通道。“channel”通常被用来描述“layer”的结构。相似的,“kernel”是被用来描述“filter”的结构。

layer和channel之间,filter和kernel之间的不同filter和kernel之间的不同很微妙。很多时候,它们可以互换,所以这可能造成我们的混淆。那它们之间的不同在于哪里呢?一个“Kernel”更倾向于是2D的权重矩阵。而“filter”则是指多个Kernel堆叠的3D结构。如果是一个2D的filter,那么两者就是一样的。但是一个3Dfilter,在大多数深度学习的卷积中,它是包含kernel的。每个卷积核都是独一无二的,主要在于强调输入通道的不同方面。讲了概念,下面我们继续讲解多通道卷积。将每个内核应用到前一层的输入通道上以生成一个输出通道。这是一个卷积核过程,我们为所有Kernel重复这样的过程以生成多个通道。然后把这些通道加在一起形成单个输出通道。下图:输入是一个5x5x3的矩阵,有三个通道。filter是一个3x3x3的矩阵。首先,filter中的每个卷积核分别应用于输入层中的三个通道。执行三次卷积,产生3个3x3的通道。然后,这三个通道相加(矩阵加法),得到一个3x3x1的单通道。这个通道就是在输入层(5x5x3矩阵)应用filter(3x3x3矩阵)的结果。同样的,我们可以把这个过程看作是一个3Dfilter矩阵滑过输入层。值得注意的是,输入层和filter有相同的深度(通道数量=卷积核数量)。3Dfilter只需要在2维方向上移动,图像的高和宽。这也是为什么这种操作被称为2D卷积,尽管是使用的3D滤波器来处理3D数据。在每一个滑动位置,我们执行卷积,得到一个数字。就像下面的例子中体现的,滑动水平的5个位置和垂直的5个位置进行。总之,我们得到了一个单一通道输出。现在,我们一起来看看,如何在不同深度的层之间转换。假设输入层有_x_in__个通道,我们想得到输出有_D_out__个通道。我们只需要将_D_out__ filters应用到输入层。每一个 filter有_D_in__个卷积核。每个filter提供一个输出通道。完成该过程,将结果堆叠在一起形成输出层。



3. 3D Convolution
在上一节的最后一个插图中,可以看出,这实际上是在完成3D卷积。但是在深度学习中,我们仍然把上述操作称为2D卷积。3D数据,2D卷积。滤波器的深度和输入层的深度是一样的。3D滤波器只在两个方向上移动(图像的高和宽),而输出也是一个2D的图像(仅有一个通道)。
3D卷积是存在的,它们是2D卷积的推广。在3D卷积中,滤波器的深度小于输入层的深度(也可以说卷积核尺寸小于通道尺寸)。所以,3D滤波器需要在数据的三个维度上移动(图像的长、宽、高)。在滤波器移动的每个位置,执行一次卷积,得到一个数字。当滤波器滑过整个3D空间,输出的结果也是一个3D的。和2D卷积能够编码2D域中的对象关系一样,3D卷积也可以描述3D空间中的对象关系。3D关系在一些应用中是很重要的,比如3D分割/医学图像重构等。
4. 1x1 Convolution
下面我们来看一种有趣的操作,1x1卷积。
我们会有疑问,这种卷积操作真的有用吗?看起来只是一个数字乘以输入层的每个数字?正确,也不正确。如果输入数据只有一个通道,那这种操作就是将每个元素乘上一个数字。但是,如果输入数据是多通道的。那么下面的图可以说明,1 x 1卷积是如何工作的。输入的数据是尺寸是H x W x D,滤波器尺寸是1 x 1x D,输出通道尺寸是H x W x 1。如果我们执行N次1x1卷积,并将结果连接在一起,那可以得到一个H x W x N的输出。1 x 1卷积在论文《Network In Network》中提出来。并且在Google发表的《Going Deeper with Convolution》中也有用到。1 x 1卷积的优势如下:降低维度以实现高效计算
高效的低维嵌入,或特征池
卷积后再次应用非线性
前两个优势可以从上图中看出。完成1 x 1卷积操作后,显著的降低了depth-wise的维度。如果原始输入有200个通道,那么1 x 1卷积操作将这些通道嵌入到单一通道。第三个优势是指,在1 x 1卷积后,可以添加诸如ReLU等非线性激活。非线性允许网络学习更加复杂的函数。

5. Convolution Arithmetic
现在我们知道了depth维度的卷积。我们继续学习另外两个方向(height&width),同样重要的卷积算法。一些术语:
Kernel size(卷积核尺寸):卷积核在上面的部分已有提到,卷积核大小定义了卷积的视图。Stride(步长):定义了卷积核在图像中移动的每一步的大小。比如Stride=1,那么卷积核就是按一个像素大小移动。Stride=2,那么卷积核在图像中就是按2个像素移动(即,会跳过一个像素)。我们可以用stride>=2,来对图像进行下采样。Padding:可以将Padding理解为在图像外围补充一些像素点。padding可以保持空间输出维度等于输入图像,必要的话,可以在输入外围填充0。另一方面,unpadded卷积只对输入图像的像素执行卷积,没有填充0。输出的尺寸将小于输入。下图是2D卷积,Kernel size=3,Stride=1,Padding=1:这里有一篇写得很好的文章,推荐给大家。它讲述了更多的细节和举了很多例子来讲述不同的Kernel size、stride和padding的组合。这里我只是总结一般案例的结果。输入图像大小是_i_,kernel size=k,padding=p,stride=s,那么卷积后的输出计算如下:
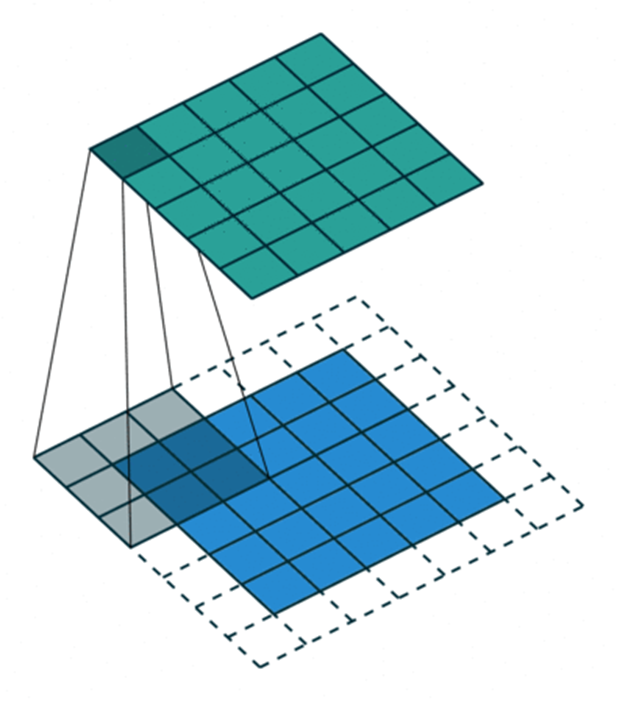
6. Transposed Convolution
在许多应用和网络架构中,我们经常想要做逆向的卷积,即要进行上采样。一些示例包括了图像高分辨率,需要将低维特征映射到高维空间,比如自动编码器或者语义分割。(对于语义分割,首先用编码器提取特征图,然后在解码器中恢复原始图像大小,这样来实现分类原始图像的每个像素。)
更直接的,可以通过应用插值方案或手动创建规则来实现上采样。现在的一些结构,像神经网络,倾向于让网络自己学习正确的转换。要实现这一点,我们可以使用Transposed Convolution。转置卷积(Transposed Convolution)在文献中也称为deconvolution或者fractionally strided convolution。但是“deconvolution”这个名字不太合适,因为Transposed Convolution毕竟不是信号/图像处理中定义的那种反卷积。从技术上讲,在信号/图像处理中deconvolution是反向的卷积操作。我们这里讲的不是这种情况。因为这,很多学者很反对将Transposed Convolution叫做deconvolution。下面我们会讲解,为什么将这种卷积操作叫做“Transposed Convolution”会更合适。我们可以使用直接卷积实现转置卷积。看下面图片中的例子,输入是2 x 2,填充2 x 2的0边缘,3 x 3的卷积核,stride=1。上采样输出大小是4 x 4。很有趣,通过填充和步长的调整,我们可以把同一张2 x 2的图像映射成不同大小的输出。下面,转置卷积应用在相同的2 x 2输入(在输入之间插入一个0)填充2 x 2边缘,stride=1。现在,输出大小为5 x 5。通过上面的例子了解转置卷积,可以帮我们建立直观的印象。但是要具体了解如何应用,就要看看在计算机中矩阵乘法是如何计算的。这样我们也可以看出,为什么Transposed Convolution是更好的名字。在卷积中,让我们定义C作为我们的卷积核,Large是输入图像,Small是卷积输出图像。完成卷积(矩阵乘法)后,我们下采样large图像,得到小的输出图像。卷积中的矩阵乘法满足C x Large=Small。下面的例子展示了该操作是怎么工作的。首先将输入变成一个16 x 1的矩阵,然后将Kernel转换成4 x 16的稀疏矩阵。在稀疏矩阵和变换后的输入间执行矩阵乘法。完成后,将得到的结果矩阵(4 x 1)转换回2 x 2输出。现在,如果我们在等式两边多次执行矩阵C转置,得到转置矩阵CT,使用矩阵与其转置矩阵的乘法给出单位矩阵的属性,得到如下的公式CT x Large=Small如下图:如你所见,我们执行了小图像到大图像的下采样。这也是我们想要得到的。现在你也明白“Transposed Convolution”的由来。
7. Dilated Convolution
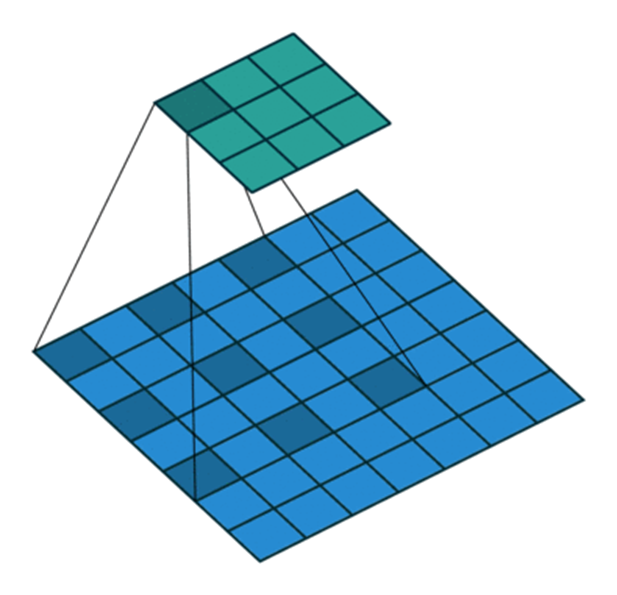
这是标准的离散卷积:
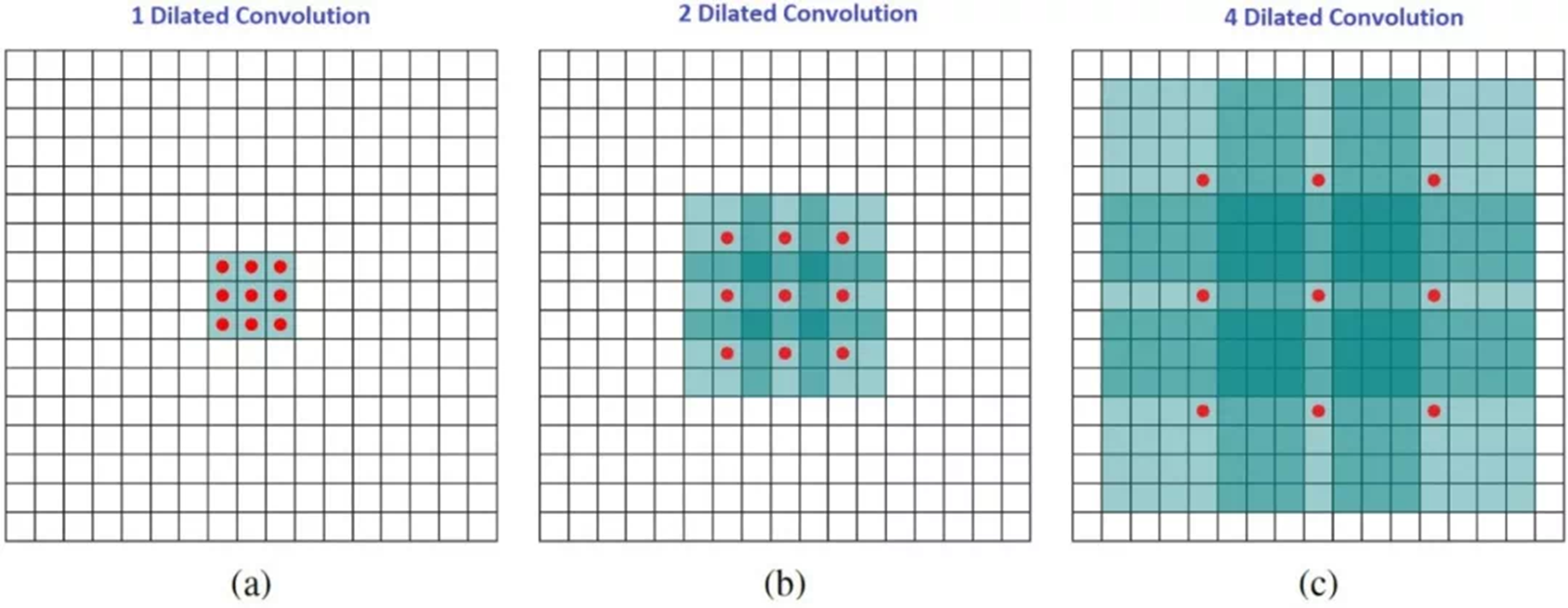
机器人厨师本尊dilated convolution如下:当_l=1_,dilated convolution称为标准离散卷积。直观地说,dilated convolutions通过在卷积核元素之间插入空格来“扩张”卷积核。扩充的参数取决于我们想如何扩大卷积核。具体实现可能会不同,但内核元素之间通常会插入l-1个空格。下面的图展示了,当kernel大小为l=1,2,4的时候。dilated convolutions的感受野,在没有增加消耗的情况下,能够观察到更大的感受野。在图中,3 x 3的红点表明,卷积后,输出图像是3x3像素。虽然三个卷积提供的输出具有相同的大小,但是模型的感受野却是不同的。当l=1时,感受野是3 x 3;l=2时,感受野是7 x7;当l=3时,感受野扩张到15 x 15。有趣的是,这些操作的相关参数数量基本相同。因此,dilated convolution被用来扩大输出的感受野,而不增加kernel的尺寸,当多个dilated convolution一个接一个堆叠时,这特别有效。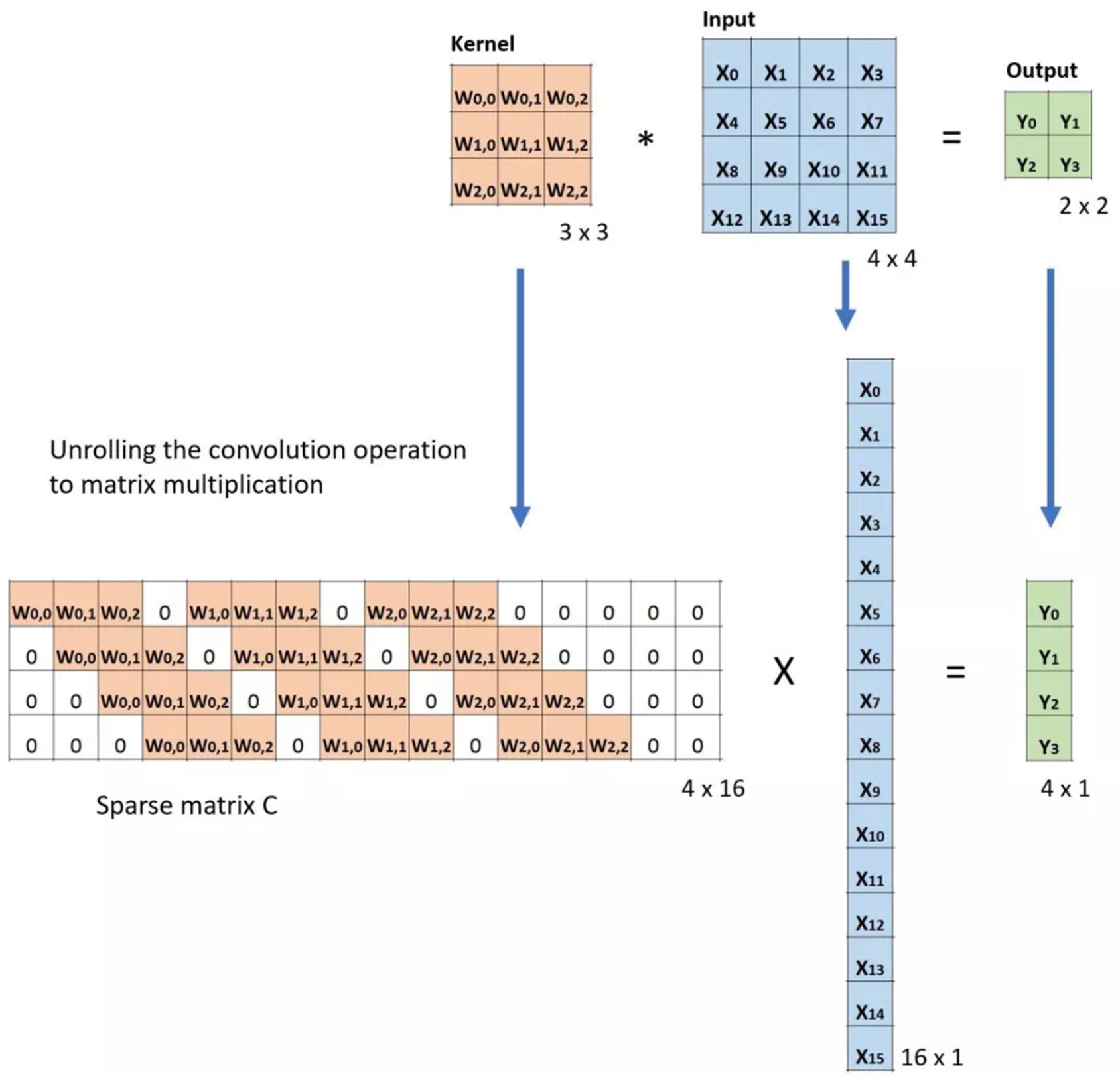


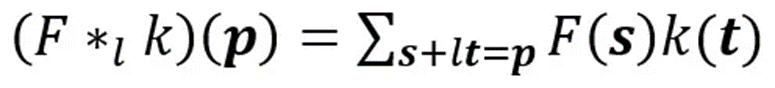
当_l=1_,dilated convolution称为标准离散卷积。
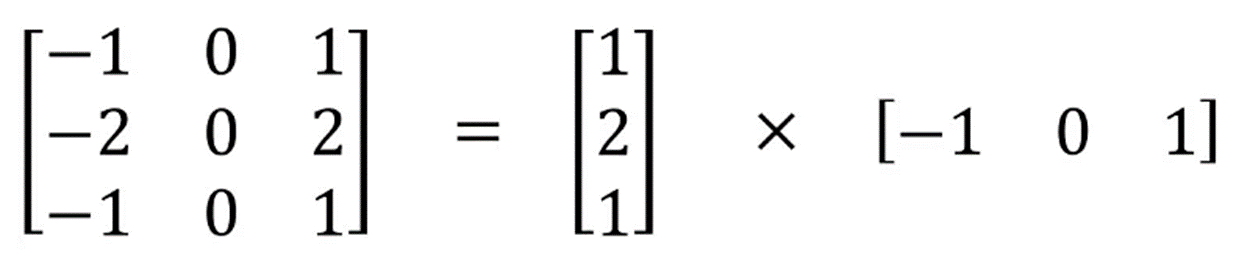

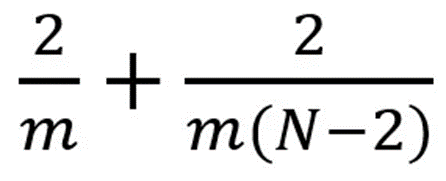




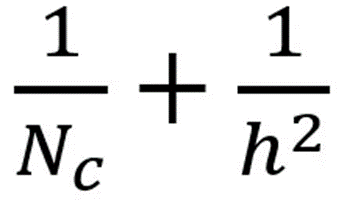
8. Separable Convolution
Separable Convolution会在一些神经网络结构中用到,比如MobileNet。有Spatially Separable Convolution 和depthwise Separable Convolution之分。
Spatially Separable Convolution
Spatially Separable Convolution在图像的2D空间维度上操作,比如高度和宽度。从概念上说,可以将该卷积操作分为两步。我们可以看下面的例子,一个Sobel kernel,3 x 3尺寸,分为3 x 1和 1 x 3的两个kernel。
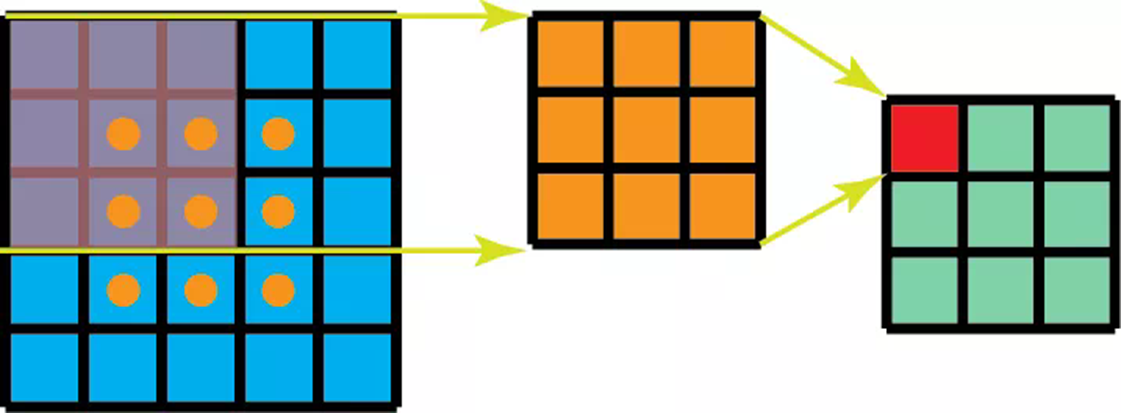
一般卷积中,是3 x 3 kernel直接和图像卷积。而Spatially Separable Convolution中,首先是3 x 1的卷积核和图像卷积, 然后再是1 x 3卷积核操作。这样一来,只需要6个参数就可以搞定了,而相同的一般卷积操作需要9个参数。更多的,在Spatially Separable Convolution中,矩阵乘法也更少。我们一起来看一个具体的例子,一个5 x 5的图像,3 x 3的卷积核(stride=1,padding=0),需要水平扫描三次,垂直扫描三次。有9个位置,可以看下图。在每个位置,9个元素要进行乘法。所以总共是要执行9 x 9=81次乘法。我们可以来看看Spatially Separable Convolution中是怎么样的。我们首先应用3 x 1的filter在5 x 5图像上。那么应该是水平扫描5个位置,垂直扫描3个位置。那么总共应该是5 x 3=15个位置,如下方有黄点的图所示。在每个位置,完成3次乘法,总共是15 x 3=45次乘法。现在我们得到的是一个3 x 5的矩阵。然后再在3 x 5矩阵上应用1 x 3kernel,那么需要水平扫描3个位置和垂直扫描3个位置。总共9个位置,每个位置执行3次乘法,那么是9 x 3=27次,所以完成一次Spatially Separable Convolution总共是执行了45+27=72次乘法,这比一般卷积要少。让我们归纳一下上面的例子。现在,我们应用卷积在一个N x N的图像上,kernel尺寸为m x m,stride=1,padding=0。传统卷积需要(N-2) x (N-2) x m+(N-2)x(N-2)xm=(2N-2)x(N-2)xm次乘法。标准卷积和Spatially Separable Convolution的计算成本比为:当有的层,图像的尺寸N远远大于过滤器的尺寸m(N>>m)时,上面的等式就可以简化为2/m。这意味着,在该种情况下,如果kernel大小为3 x 3,那么Spatially Separable Convolution的计算成本是传统卷积的2/3。虽然Spatially Separable Convolution可以节省成本,但是它却很少在深度学习中使用。最主要的原因是,不是所有的kernel都可以被分为两个更小的kernel的。如果我们将所有传统卷积用Spatially Separable Convolution替代,那么这将限制在训练过程中找到所有可能的kernels。找到的结果也许就不是最优的。Depthwise Separable Convolution
现在让我们再来看看Depthwise Separable Convolution,这在深度学习中就应用得更多一些了。该卷积也是分两步,DW卷积和1 x 1卷积。
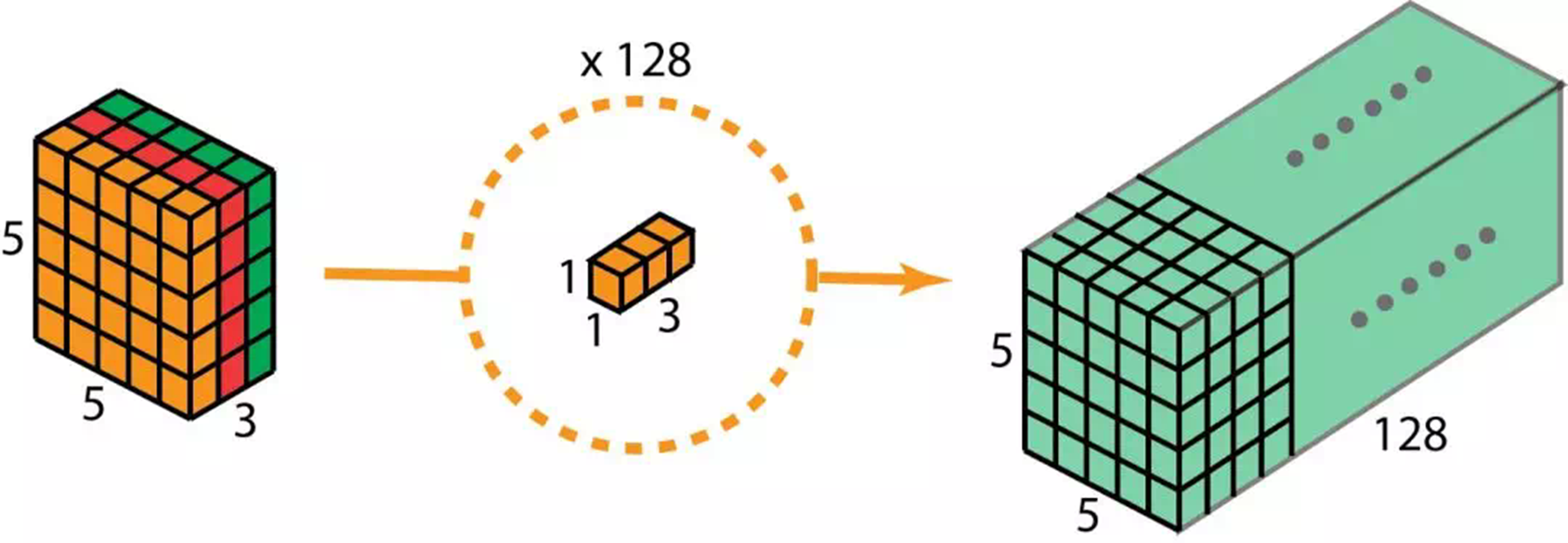
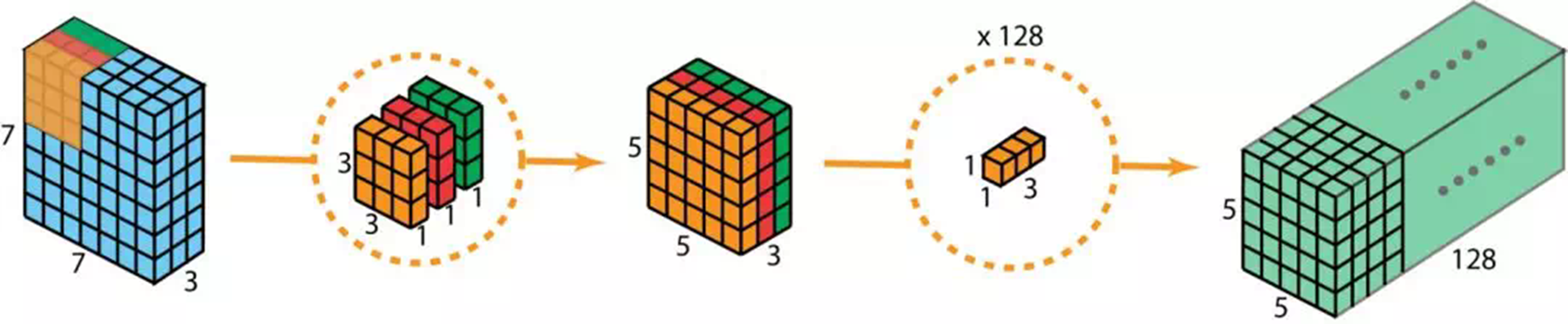
在讲解这步骤之前,我们有必要回顾一下上面提到的2D卷积和1 x 1卷积。让我们快速过一下标准2D卷积。直接看具体的案例,输入的大小是7 x 7 x 3(高、宽、通道数)。卷积核大小3 x 3 x 3。完成2D卷积操作之后,输出是5 x 5 x 1(只有一个通道)。一般的,两个网络层之间会有多个过滤器。这里我们有128个过滤器。在应用128个2D卷积后,我们有128个5 x 5 x 1的输出特征图。我们然后将这些特征图堆叠到单层,大小为5 x 5 x 128。通过该操作,我们将输入(7 x 7 x 3)的转换成了5 x 5 x 128的输出。在空间上,高度和宽度都压缩了,但是深度拓展了。128个filter,将输出扩展到128层现在我们看看使用depthwise separable convolution ,让我们看看如何获得相同的转换效果。首先,我们将deothwise convolution应用到输入层。和使用单一3 x 3 x 3filter在2D卷积上不同,我们使用3个分开的kernel。每个kernel的尺寸是3 x 3 x 1。每个kernel只完成输入的单通道卷积。每个这样的卷积操作会得到一个5 x 5 x 1的特征图。然后,我们将三个特征图堆叠到一起,得到一个5 x 5 x 3的图像。操作结束,输出的大小为5 x 5 x 3。我们压缩了空间维度,但是输出的深度和输入是一样的。depthwise separable convolution的第二步是,扩充深度,我们使用大小为1 x 1 x 3的kernel,完成1 x 1卷积。最后得到5 x 5 x 1的特征图。在完成128个1 x 1卷积操作之后,我们得到了5 x 5 x 128的层。通过上面的两步,deothwise separable convolution将输入(7 x 7 x 3)的转换成了5 x 5 x 128的输出。整个过程如下图:因此,deothwise separable convolution的优势是什么呢?效率!比起2D卷积,deothwise separable convolution要少很多操作。让我们来看看2D卷积的计算消耗。有128个3 x 3 x 3卷积核,移动5 x 5次。一共要执行128 x 3 x 3 x 3 x 5 x 5=86400乘法。separable convolution呢?在第一步deothwise convolution中,这里有3个3 x 3 x 1kernel,移动5 x 5次,一共是675次乘法。在第二步中,128个1 x 1 x 3卷积核移动5 x 5次,一共9600次乘法。总的计算消耗是675+9600=10275次乘法。消耗仅仅只有2D卷积的12%。因此,随意一张图的处理,应用deothwise separable convolution可以节省多少时间呢?让我们根据上面的案例做一般推导。现在,假设输入是H x W x D,2D卷积(stride=1,padding=0)Nc个kernel大小为h x h x D,其中h是偶数。将输入H x W x D转换为输出层(H-h+1 x W-h+1 x Nc)。总的乘法操作是:Nc x h x h x D x (H-h+1) x (W-h+1)。另一方面,使用depthwise separable convolution的计算消耗是:D x h x h x 1 x (H-h+1) x (W-h+1) + Nc x 1 x 1 x D x (H-h+1) x (W-h+1) = (h x h + Nc) x D x (H-h+1) x (W-h+1)后者和前者的计算消耗比例为:在现在的很多结构中,输出层都有相当多的通道。也就是说_Nc_往往远大于h。所以,如果是3 x 3的filter,那么2D卷积花的时间是depthwise separable convolution的9倍,如果是5 x 5的卷积核,将是25倍。depthwise separable convolution的劣势是什么呢?它减少了卷积的参数。如果是一个较小的模型,那么模型的空间将显著减小。这造成的结果就是,模型得到的结果并不是最优。
LLVM中矩阵Matrix的实现分析
1 背景说明
Clang提供了C/C++语言对矩阵的扩展支持,以方便用户使用可变大小的二维数据类型来实现计算,目前该特性还是实验版,设计和实现都在变化中。LLVM目前设计为支持小型列矩阵(column major),其对矩阵的设计基于向量。为用户提供向量代码生成功能,能够减少不必要的内存访问,并且提供用户友好的接口。本文基于LLVM13以Intel X86架构为平台,来实验和分析LLVM编译器对矩阵运算的基础支持。
LLVM目前支持的矩阵间运算包括矩阵转置、矩阵加减法和矩阵乘法,矩阵除法只支持矩阵除以标量,不支持矩阵与矩阵相除。
2 功能实现
2.1 数据实现
矩阵支持的元素类型有整型、单精、双精、半精,用户可以通过matrix_type属性来定义各种不同元素类型不同行列数的矩阵。

2.2 内建支持
2.2.1 Clang
Clang前端提供了3个内建接口供用户使用,如下表所示,目前矩阵的load和store都是按列操作,未来对行矩阵(row major)的支持也在计划中。

当从一个基地址*ptr加载矩阵时,列矩阵(column major)是一列一列依次赋值的。下图展示了跨步为5时, 列矩阵(column major)的load和store操作。

2.2.1 LLVM
LLVM后端提供了int_matrix_multiply内建函数,该接口并未在Clang前端暴露,用户在编码矩阵乘计算时,只需要使用乘法符号(*),LLVM在创建中间表示(IR)的时候会自动创建对该内建函数的调用。
2.3 算法流程
通过clang -cc1 -fenable-matrix -emit-llvm matrix_load.c编译代码,生成的IR中包含对内建接口的调用。


Clang中的3个内建接口是用户编码过程中可以直接调用的,所以它们的IR的生成过程是走的内建解析,矩阵乘在用户编码时并不是函数调用,所以走的是标量乘法解析,在其中增加了矩阵类型的分支。
以下是CreateColumnMajorLoad函数的详细代码。


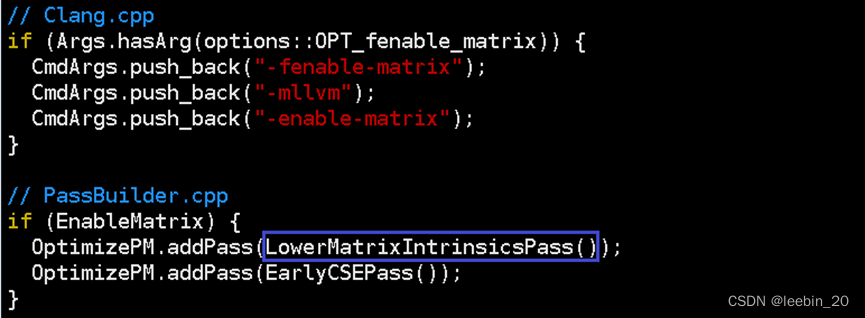
实际上LLVM X86中矩阵操作最终都是转成向量来做的,所以这一步生成的IR还需要进一步降级,使用向量指令替换内建接口的调用指令,并且对已经替换的接口指令做了缓存,下次再次调用同类矩阵接口指令,可以直接从缓存中取向量指令,而不需要再去执行矩阵转向量的操作,从而提高性能。通过clang -fenable-matrix -emit-llvm –S matrix_load.c可以生成最终的IR,该命令行在Clang.cpp中给后端传递了-enable-matrix选项,该选项会在PassBuilder.cpp中添加LowerMatrixIntrinsicsPass优化,该优化将上述IR中的矩阵操作转换成向量操作。
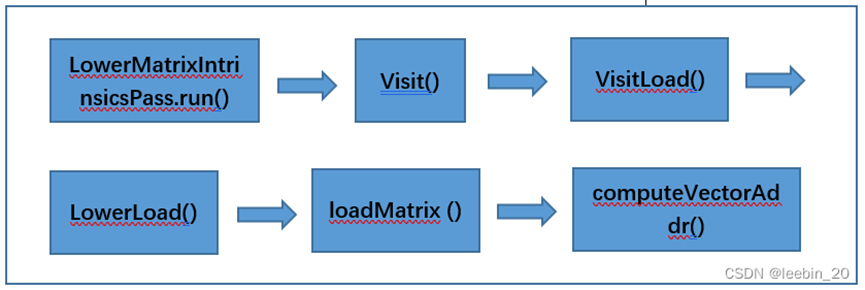
假设一个4x4的矩阵如下所示,现在需要以11为基址,从中计算一个2x3的子矩阵,LLVM提供了computeVectorAddr函数来计算子矩阵的地址。BasePtr指矩阵(向量)起始元素地址,VecIdx指当前向量在子矩阵中的index,Stride指加载时的跨步,NumElements指每个向量中的元素个数,EltType指元素类型。函数中VecStart变量通过VecIdx跟Stride相乘得到,该变量表示当前计算的向量的起始位置,比如示例矩阵中13对应的VecStart = 2 * 4 = 8;如果VecStart = 0,则代表是第0列向量,此时将BasePtr赋给VecStart作为新向量的起始地址,如果VecStart != 0,则通过Builder.CreateGEP()创建一个IR操作getelementptr,取对应列首地址,以此类推;最后通过Builder.CreatePointerCast()把上述列的首地址转成VecPtrType对应的向量地址,这样新向量就生成了。


有了以上computeVectorAddr函数,只要给定相应的参数,就可以计算出一个向量(子矩阵)的地址了,调用过程如下所示。LLVM中在load矩阵时,便是根据矩阵的列数(行矩阵根据行数)来依次生成原始矩阵对应的向量,比如一个int 5x4的矩阵会被load为4个<5 x i32>向量,而一个int 4x5的矩阵会被load为5个<4 x i32>向量。
矩阵的加减法是对应位置元素加减,所以在拆成向量后,即可以复用向量的加减操作,乘法与加减法的运算规则不同,所以需要对拆出来的向量进一步处理。假设矩阵A乘矩阵B等于矩阵C,元素类型都是int,如下所示。

load的时候矩阵A被拆成了4个<5 x i32>向量,矩阵B被拆成了5个<4 x i32>向量,LLVM会根据拆分后的向量的地址把向量进一步整合成适合目标架构宽度乘法运算的新向量,具体是通过目标架构寄存器宽度和当前向量元素类型宽度的比值得出要整合的向量的大小。当前x86架构这里的VF返回的是4,也就是说以4个元素为一组向量整合矩阵A和矩阵B,整合完成后进行向量运算,如下所示。
<A00,A10,A20,A30>x<B00,B00,B00,B00>+
<A01,A11,A21,A31>x<B10,B10,B10,B10>+
<A02,A12,A22,A32>x<B20,B20,B20,B20>+
<A03,A13,A23,A33>x<B30,B30,B30,B30>=
<C00,C10,C20,C30>
可以看到,C40还没有被计算出来,此时就剩1个元素需要计算了,于是把矩阵A每一列最后1个元素和矩阵B第一列每个元素转成<1 x i32>向量,然后对应元素相乘后再相加,从而完成计算。
<A40>x<B00>+<A41>x<B10>+<A42>x<B20>+<A43>x<B30>=<C40>
那么是如何得到最后的向量是<1 x i32>类型呢?如前所述,VF决定了整合的向量的元素个数,LLVM通过以下代码来实现,C = 4,R = 5,当I + BlockSize > R时,会不断对BlockSize取半,确保了除1以外的其它向量元素个数都是偶数,BlockSize初值为4,第0列第0行时,I + BlockSize = 4 < R,所以取4个元素作为一组向量,第0列第5行时,I + BlockSize = 8 > R,BlockSize在while循环中最终算得1后满足条件。

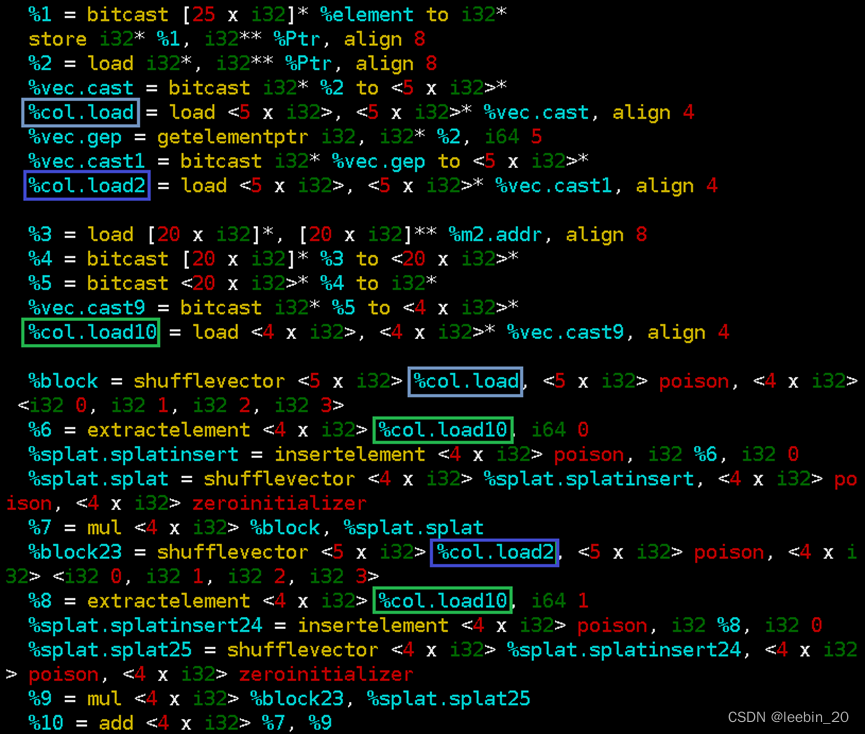
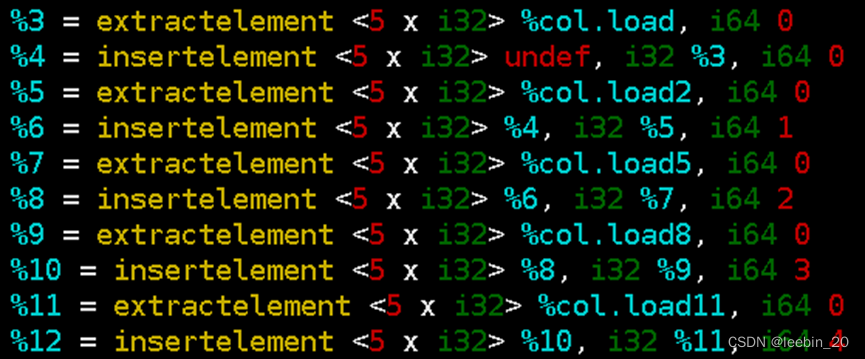
实际在IR中使用了shufflevector、extractelement和insertelement来生成新的向量。如下代码所示,%col.load为矩阵A第0列元素,%col.load2为矩阵A第1列元素,%col.load10为矩阵B第0列元素,从%col.load中取4个元素依次与%col.load10中的第0个元素相乘,从%col.load2中取4个元素依次与%col.load10中的第1个元素相乘,再把乘积依次相加。

key value
%block < A00,A10,A20,A30>
%splat.splat < B00,B00,B00,B00>
%block23 < A01,A11,A21,A31>
% splat.splat25 < B10,B10,B10,B10>

3 举例说明
3.1 Matrix load
编写一段测例matrix_load.c如下所示,通过matrix_type属性指定行列数定义5x5的int类型矩阵,跨步设为5,这样正好把数组中的25元素都加载到矩阵中。
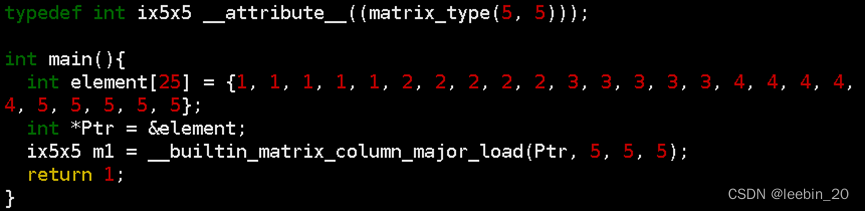
生成的IR正如前文所述,首先每次从数组element中取出5个元素组成一个向量。
再依次存到m1对应的矩阵的地址里。

生成的汇编部分截图如下所示,可以看到,长度25的数组元素被拆成4+4+4+4+4+4+1取出来放到对应地址,存的时候按照4+1作为一组存了5次,正好构成5x5的矩阵。

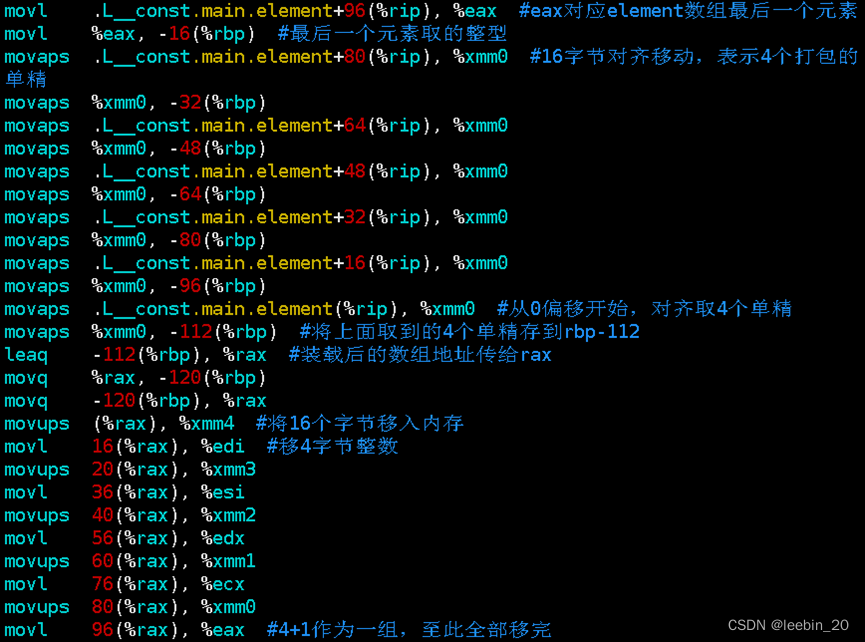
3.3 Matrix transpose
矩阵转置同样也是将矩阵操作转换为向量操作,编写测例如下所示。

以下是生成的部分IR,从矩阵中load出每一列向量,第0列第0个元素插入到%4代表的<5 x double>新向量第0位置,第1列第0个元素插入到%4第1位置,第2列第0个元素插入到%4第2个位置,依次提取,按序插入,这样就完成了矩阵的转置操作。
参考文献链接
https://mp.weixin.qq.com/s/sr3D_DXvF1lqufdb5U5z0g
https://blog.csdn.net/leebin_20/article/details/128394980





