标准自编码器(TensorFlow实现)
由 Hinton 提出的标准自动编码机(标准自编码器)只有一个隐藏层,隐藏层中神经元的数量少于输入(和输出)层中神经元的数量,这会压缩网络中的信息,因此可以将隐藏层看作是一个压缩层,限定保留的信息。
自动编码机的学习包括在隐藏层上对输入信号进行压缩表示,然后在输出层尽可能地复现原始输入:
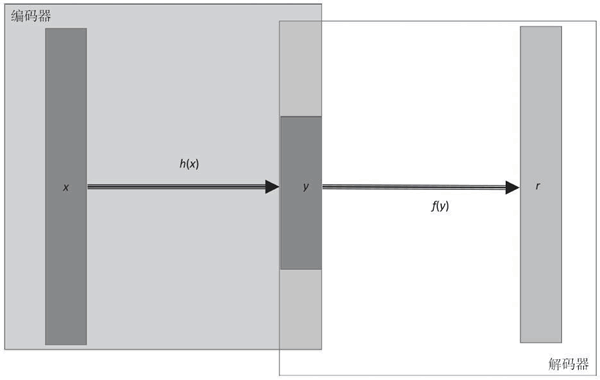
图 1 单隐藏层的自动编码机
本节利用自动编码机进行图像重构,将利用 MNIST 数据训练自动编码机,并使用它来重构测试图像。
具体做法
-
导入所有必要的模块:

-
从 TensorFlow 中获取 MNIST 数据,这里要注意的一点是,标签并没有进行独热编码,因为并没有使用标签来训练网络。自动编码机是通过无监督学习进行训练的:

-
声明 AutoEncoder 类,使用 init 方法初始化自动编码机的权重、偏置和占位符,也可以在 init 方法中构建全部的计算图。还需要定义编码器、解码器,set_session(会话建立)和 fit 方法。此处构建的自动编码机使用简单的均方误差作为损失函数,使用 AdamOptimizer 进行优化:

为便于使用,此处还定义了两个辅助函数,reduced_dimension 给出编码器网络的输出,reconstruct 给出重构的测试图像的输出。
-
训练时将输入数据转换为 float 型,初始化所有变量并运行会话。在计算时,目前只是测试自动编码机的重构能力:

-
绘制误差在训练周期中的变化图,验证网络的均方误差在训练时是否得到优化,对于一个好的训练,误差应该随着训练周期的增加而减少:

图示如下:
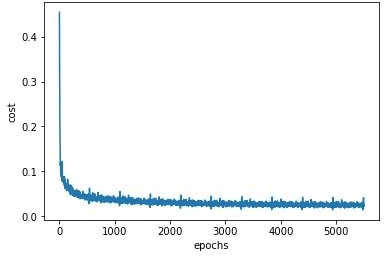
可以看到,随着网络的学习,损失/成本是下降的,当训练周期达到 5000 时,几乎是在一条线上振荡,这意味着进一步增加训练周期将不再有用。如果现在还想要改进模型,应该调整学习率、批量大小和优化器等超参数。
-
观察重构的图像,对比原始图像和自动编码机生成的重构图像:

得到以下结果:

解读分析
有意思的是,在前面的代码中,维数从输入的 784 降到了 256,但是网络仍然可以重构原始图像。将自动编码机性能与 RBM 进行对比,其中隐藏层维数相等:

可以看到,由自动编码机重构的图像比 RBM 重构的图像要清晰得多。原因在于自动编码机中有更多的权重(从隐藏层到解码器输出层的权重)被训练。自动编码机学到的细节更多,即使两者都将信息压缩到相同的尺寸,其性能也优于 RBM。
知识扩展
像 PCA 一样,自动编码机也可以用于降维,但 PCA 只能进行线性变换,而自动编码机可以使用非线性激活函数,从而在其中引入非线性变换。
下图是 Hinton 的论文“Reducing the dimensionality of data with Neural Networks”复现的结果,图 A 显示 PCA 的结果,图 B 是由 RBM 堆叠的自动编码机(每层节点为 784-1000-500-250-2)的结果:
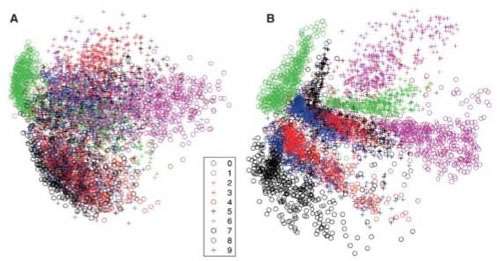
正如稍后会看到的,使用堆叠自动编码机时,每个自动编码机最初会独立进行预训练,然后会对整个网络进行微调以获得更好的性能。
人工智能芯片与自动驾驶





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· 没有源码,如何修改代码逻辑?
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· .NET10 - 预览版1新功能体验(一)