个性化排序的神经协同过滤

个性化排序的神经协同过滤

Neural Collaborative Filtering for Personalized Ranking

这一部分将超越显式反馈，介绍神经协作过滤（NCF）框架，用于推荐具有隐式反馈。隐式反馈在推荐系统中普遍存在。诸如点击、购买和观看等行为都是常见的隐性反馈，这些反馈很容易收集并指示用户的偏好。我们将介绍的模型名为NeuMF[He et al.，2017b]，是神经矩阵分解的缩写，旨在解决带有隐式反馈的个性化排名任务。该模型利用神经网络的灵活性和非线性，代替矩阵分解的点积，提高模型的表达能力。具体地说，该模型由广义矩阵分解（GMF）和多层感知器（MLP）两个子网络构成，用两条路径来模拟相互作用，而不是简单的内积。将这两个网络的输出连接起来，以计算最终的预测分数。与AutoRec中的评分预测任务不同，该模型基于隐含反馈为每个用户生成一个排名推荐列表。我们将使用最后一节介绍的个性化排名损失来训练这个模型。

1. The NeuMF model

如上所述，NeuMF融合了两个子网。GMF是矩阵分解的一种神经网络模型，输入是用户和项目潜在因素的元素乘积。它由两个神经层组成：

 

这个模型的另一个组件是MLP。为了增加模型的灵活性，MLP子网不与GMF共享用户和项嵌入。它使用用户和项嵌入的连接作为输入。通过复杂的连接和非线性变换，它能够模拟用户和物品之间的复杂交互。更准确地说，MLP子网定义为：

 

 

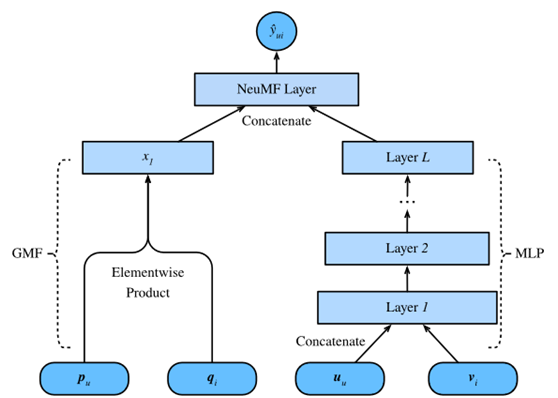
 Fig. 1  Illustration of the NeuMF model

from d2l import mxnet as d2l

from mxnet import autograd, gluon, np, npx

from mxnet.gluon import nn

import mxnet as mx

import random

import sys

npx.set_np()

2. Model Implementation

下面的代码实现了NeuMF模型。它由一个广义矩阵分解模型和一个具有不同用户和项目嵌入向量的多层感知器组成。MLP的结构由参数nums_hiddens控制。ReLU用作默认激活功能。

class NeuMF(nn.Block):

    def __init__(self, num_factors, num_users, num_items, nums_hiddens,

                 **kwargs):

        super(NeuMF, self).__init__(**kwargs)

        self.P = nn.Embedding(num_users, num_factors)

        self.Q = nn.Embedding(num_items, num_factors)

        self.U = nn.Embedding(num_users, num_factors)

        self.V = nn.Embedding(num_items, num_factors)

        self.mlp = nn.Sequential()

        for num_hiddens in nums_hiddens:

            self.mlp.add(nn.Dense(num_hiddens, activation='relu',

                                  use_bias=True))

    def forward(self, user_id, item_id):

        p_mf = self.P(user_id)

        q_mf = self.Q(item_id)

        gmf = p_mf * q_mf

        p_mlp = self.U(user_id)

        q_mlp = self.V(item_id)

        mlp = self.mlp(np.concatenate([p_mlp, q_mlp], axis=1))

        con_res = np.concatenate([gmf, mlp], axis=1)

        return np.sum(con_res, axis=-1)

3. Customized Dataset with Negative Sampling

对于成对排序损失，一个重要的步骤是负采样。对于每个用户，用户未与之交互的项是候选项（未观察到的条目）。下面的函数以用户身份和候选项作为输入，并从每个用户的候选项集中随机抽取负项。在训练阶段，该模型确保用户喜欢的项目的排名高于其不喜欢或未与之交互的项目。

class PRDataset(gluon.data.Dataset):

    def __init__(self, users, items, candidates, num_items):

        self.users = users

        self.items = items

        self.cand = candidates

        self.all = set([i for i in range(num_items)])

    def __len__(self):

        return len(self.users)

    def __getitem__(self, idx):

        neg_items = list(self.all - set(self.cand[int(self.users[idx])]))

        indices = random.randint(0, len(neg_items) - 1)

        return self.users[idx], self.items[idx], neg_items[indices]

4. Evaluator

在这一部分中，我们采用按时间分割的策略来构造训练集和测试集。给定截线命中率的两个评价指标ℓℓ (Hit@ℓHit@ℓ) and area under the ROC curve (AUC)，用ROC曲线下面积（AUC）评价模型的有效性。给定位置命中率ℓ，对于每个用户，指示建议的项目是否包含在顶部ℓ排行榜。正式定义如下：

 

#@save

def hit_and_auc(rankedlist, test_matrix, k):

    hits_k = [(idx, val) for idx, val in enumerate(rankedlist[:k])

              if val in set(test_matrix)]

    hits_all = [(idx, val) for idx, val in enumerate(rankedlist)

                if val in set(test_matrix)]

    max = len(rankedlist) - 1

    auc = 1.0 * (max - hits_all[0][0]) / max if len(hits_all) > 0 else 0

return len(hits_k), auc

然后，总体命中率和AUC计算如下。

#@save

def evaluate_ranking(net, test_input, seq, candidates, num_users, num_items,

                     ctx):

    ranked_list, ranked_items, hit_rate, auc = {}, {}, [], []

    all_items = set([i for i in range(num_users)])

    for u in range(num_users):

        neg_items = list(all_items - set(candidates[int(u)]))

        user_ids, item_ids, x, scores = [], [], [], []

        [item_ids.append(i) for i in neg_items]

        [user_ids.append(u) for _ in neg_items]

        x.extend([np.array(user_ids)])

        if seq is not None:

            x.append(seq[user_ids, :])

        x.extend([np.array(item_ids)])

        test_data_iter = gluon.data.DataLoader(gluon.data.ArrayDataset(*x),

                                               shuffle=False,

                                               last_batch="keep",

                                               batch_size=1024)

        for index, values in enumerate(test_data_iter):

            x = [gluon.utils.split_and_load(v, ctx, even_split=False)

                 for v in values]

            scores.extend([list(net(*t).asnumpy()) for t in zip(*x)])

        scores = [item for sublist in scores for item in sublist]

        item_scores = list(zip(item_ids, scores))

        ranked_list[u] = sorted(item_scores, key=lambda t: t[1], reverse=True)

        ranked_items[u] = [r[0] for r in ranked_list[u]]

        temp = hit_and_auc(ranked_items[u], test_input[u], 50)

        hit_rate.append(temp[0])

        auc.append(temp[1])

    return np.mean(np.array(hit_rate)), np.mean(np.array(auc))

5. Training and Evaluating the Model

培训功能定义如下。我们以成对的方式训练模型。

#@save

def train_ranking(net, train_iter, test_iter, loss, trainer, test_seq_iter,

                  num_users, num_items, num_epochs, ctx_list, evaluator,

                  candidates, eval_step=1):

    timer, hit_rate, auc = d2l.Timer(), 0, 0

    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0, 1],

                            legend=['test hit rate', 'test AUC'])

    for epoch in range(num_epochs):

        metric, l = d2l.Accumulator(3), 0.

        for i, values in enumerate(train_iter):

            input_data = []

            for v in values:

                input_data.append(gluon.utils.split_and_load(v, ctx_list))

            with autograd.record():

                p_pos = [net(*t) for t in zip(*input_data[0:-1])]

                p_neg = [net(*t) for t in zip(*input_data[0:-2],

                                              input_data[-1])]

                ls = [loss(p, n) for p, n in zip(p_pos, p_neg)]

            [l.backward(retain_graph=False) for l in ls]

            l += sum([l.asnumpy() for l in ls]).mean()/len(ctx_list)

            trainer.step(values[0].shape[0])

            metric.add(l, values[0].shape[0], values[0].size)

            timer.stop()

        with autograd.predict_mode():

            if (epoch + 1) % eval_step == 0:

                hit_rate, auc = evaluator(net, test_iter, test_seq_iter,

                                          candidates, num_users, num_items,

                                          ctx_list)

                animator.add(epoch + 1, (hit_rate, auc))

    print('train loss %.3f, test hit rate %.3f, test AUC %.3f'

          % (metric[0] / metric[1], hit_rate, auc))

    print('%.1f examples/sec on %s'

          % (metric[2] * num_epochs / timer.sum(), ctx_list))

现在，我们可以加载MovieLens 100k数据集并训练模型。由于在MovieLens数据集中只有评级，但准确性会有所下降，因此我们将这些评级进行二值化，即0和1。如果一个用户对一个项目进行评分，我们认为隐含反馈为1，否则为零。给一个项目评分的行为可以看作是一种提供隐性反馈的形式。在这里，我们在seq感知模式下分割数据集，在这种模式下，用户的最新交互项被排除在外进行测试。

batch_size = 1024

df, num_users, num_items = d2l.read_data_ml100k()

train_data, test_data = d2l.split_data_ml100k(df, num_users, num_items,

                                              'seq-aware')

users_train, items_train, ratings_train, candidates = d2l.load_data_ml100k(

    train_data, num_users, num_items, feedback="implicit")

users_test, items_test, ratings_test, test_iter = d2l.load_data_ml100k(

    test_data, num_users, num_items, feedback="implicit")

num_workers = 0 if sys.platform.startswith("win") else 4

train_iter = gluon.data.DataLoader(PRDataset(users_train, items_train,

                                             candidates, num_items ),

                                   batch_size, True,

                                   last_batch="rollover",

                                   num_workers=num_workers)

然后我们创建并初始化模型。我们使用一个三层MLP，隐藏大小恒定为10。

ctx = d2l.try_all_gpus()

net = NeuMF(10, num_users, num_items, nums_hiddens=[10, 10, 10])

net.initialize(ctx=ctx, force_reinit=True, init=mx.init.Normal(0.01))

下面的代码训练模型。

The following code trains the model.

lr, num_epochs, wd, optimizer = 0.01, 10, 1e-5, 'adam'

loss = d2l.BPRLoss()

trainer = gluon.Trainer(net.collect_params(), optimizer,

                        {"learning_rate": lr, 'wd': wd})

train_ranking(net, train_iter, test_iter, loss, trainer, None, num_users,

              num_items, num_epochs, ctx, evaluate_ranking, candidates)

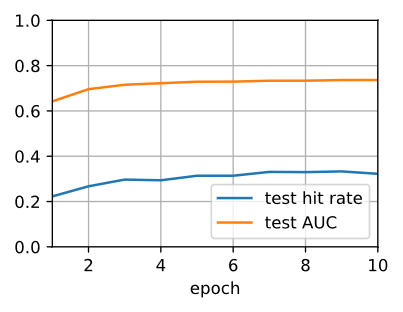
train loss 4.030, test hit rate 0.322, test AUC 0.736

13.1 examples/sec on [gpu(0), gpu(1)]

 

6. Summary

• Adding nonlinearity to matrix factorization model is beneficial for improving the model capability and effectiveness.
• NeuMF is a combination of matrix factorization and Multilayer perceptron. The multilayer perceptron takes the concatenation of user and item embeddings as the input.