new_hope网络流

网络流与费用流

——new_hope

---

一、流网络

1.形式化定义：

设 \(G = (V,E)\) 为一个流网络，\(s\)，\(t\) 分别为网络的源节点和汇点，容量函数 \(c\)，流函数 \(f\)，满足以下性质：

• 容量限制：\(\forall u, v \in V, 0 \le f(u,v) \le c(u,v)\)，当 \((u,v) \notin E\) 时，\(f(u,v) = 0\)
• 流量守恒：\(\forall u \in V - \{ s, t\}, \sum_{v \in V} f(v,u) = \sum_{v \in V} f(u,v)\)

wuhupai注:前一个 \(\sum\) 的意思就是所有流向 \(u\) 的东西，后一个 \(\sum\) 说的是从 \(u\) 流出去的所有东西，这显然是对的

值得注意的是，若流网络的边集 \(E\) 包含一条边 \((u,v)\)，则不存在反方向的边 \((v,u)\)，所以对于流量守恒这一性质的理解应是，对于一个点 \(u\)，流入量等于流出量，那么对于整张网络而言，便有全局流入量等于全局流出量，而并非正反两条边流量相等。（形式化的定义容易带偏理解）

我们定义流网络 \(G\) 的一个流 \(f\) 的值 \(|f|\) 如下：

\[|f| = \sum_{u \in V}f(s,u) - \sum_{u \in V}f(u,s) \]

即流入源节点 \(s\) 的流之和 - 流出源节点 \(s\) 的流之和，通常情况下，右边的求和项为 \(0\)（没有流入 \(s\) 的流量），而这个完整的式子接下来会用到。

2.两个简单的转化：

1. 反平行边：
   流网络中，若 \((u,v) \in E\)，则 \((v,u) \notin E\)，但实际情况中，若图同时存在 \((u, v)\) 和 \((v,u)\)，则称这两条边为反平行边，我们可以通过分裂其中一条反平行边，加入新节点，从而得到与原图等价的网络【画图说明】。（这里不能简单等价为一条容量为 \(c(u,v) - c(v,u)\) 的边）
2. 超级源点与超级汇点：
   若一张网络有多个源点与多个汇点，则可通过加入超级源点与超级汇点，设容量为正无穷，显然地，这样得到的网络与原图等价。

3.思考题

假定除边的容量外，流网络还有节点容量，记为 \(l(v)\)，则如何构造除一个带有节点容量的流网络 \(G'\) 转化为一个等价的不带有节点容量的流网络 \(G\)。

\({拆点,加边} 【画图说明】\)

---

二、最大流问题与解决思想、实现算法

1. 概念引入：

1. 残存网络
   设残存网络 \(G_f\)，\(G_f\) 由仍有空间对流量 \(f\) 进行调整的边构成。但同时，为了试探更大的流量，可能会需要有对正流量 \(f(u,v)\) 的缩减，此时则需要引入原图 \(G\) 中没有的边，利用反向流量抵消正向流量，从而达到缩减。
   因此，我们形式化地将残存网络 \(G_f\) 中的残存容量定义为：
   \[c_f(u,v) = \begin{cases} c(u,v) - f(u,v) & (u,v) \in E \\ f(v,u) & (v,u) \in E \end{cases}\]
   而根据流网络性质，\(c_f(u,v)\) 仅会取到上述的一个值。【画图说明】
   由图可以看出，残存“网络”出现了反平行边，不符合流网络的定义，但除此以外都符合流网络的性质。
   设 \(f'\) 为 \(G_f\) 中的一个流，定义 \(f \uparrow f'\) 为 \(f'\) 对 \(f\) 的递增，形式如：
   \[(f \uparrow f')(u, v) = f(u,v) + f'(u, v) - f'(v, u),(u,v) \in E \]
   (即边 \((u,v)\) 的流量增加 \(f'(u,v)\)，又减少了 \(f'(v,u)\))
   根据数学推导，可以得到 \(f \uparrow f'\) 是 \(G\) 中的一个流(满足流量守恒和容量限制)，且 \(|f \uparrow f| = |f| + |f'|\)
   
   
2. 增广路径
   给定流网络 \(G = (V, E)\) 和流 \(f\)，增广路径 \(p\) 是残存网络 \(G_f\) 中一条从源点 \(s\) 到汇点 \(t\) 的简单路径。定义在一条增广路径 \(p\) 上能够为每条边增加的流量的最大值为 \(p\) 的残存容量(注意与残存网络中残存容量的区分)，记作：
   \[c_f(p) = \min(c_f(u,v):(u,v) \in p) \]
   可以很直观地感受到，当 \(f\) 增加了大小为 \(c_f(p)\) 的流时，\(f\) 越接近最大流。
   
   
3. 流网络的切割
   流网络 \(G = (V,E)\) 中的一个切割 \((S,T)\) 将点集 \(V\) 划分为 \(S\) 和 \(T = V - S\) 两个集合，使得 \(s \in S\), \(t \in T\)。定义横跨切割 \((S,T)\) 的净流量 \(f(S,T)\) 如下：
   wuhupai注：这其实就是在这个截面上流过去的流，这个流是流过去的减流回来的
   \[f(S,T) = \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T}f(v,u) \]
   切割 \((S,T)\) 的容量是：
   \[c(S,T) = \sum_{u \in S}\sum_{v \in T}c(u,v) \]
   还是一样的，\((u,v) 和 (v,u)\) 只能有其中一条在 \(E\) 中，不存在的一条，其 \(|f| = 0\)。
   一个网络的最小切割是整个网络中 \({容量最小}\) 的切割。
   我们可以发现，切割容量只计算了从 \(S\) 到 \(T\) 的容量和，这与流的定义有所区别。
   wuhupai注：这就是从 \(S\) 流向 \(T\) 的流量减去从 \(T\) 流向 \(S\) 的流量
   wuhupai注：切割就是将一个图分成两半
   wuhupai注：切割的容量就是在这个横截面上的边的容量之和

2. 引理证明【重要】：

1. 对于给定的流 \(f\)，横跨任何切割的净流量都相同，都等于 \(|f|\)。
   wuhupai注：我喜欢感性理解，不妨将这张图看成一个并联电路，那么支路电流之和就等于干路电流。我任选一些支路，电流之和就等于干路电流
   \(\triangle\)证明如下：
   重写流量守恒式，\(\forall u \in V - \{s, t\}\)

   \[\sum_{v \in V} f(v,u) - \sum_{v \in V} f(u,v) = 0 \]

   根据 \(|f|\) 定义，加入上式(针对 \(S - \{s\}\) 部分的求和)，

   \[|f| = \sum_{v \in V}{f(s,v)} - \sum_{v \in V}{f(v,s)} + \sum_{v \in S - \{s\}} \left( \sum_{v \in V}{f(v,u)} - \sum_{v \in V}{f(u,v)} \right) \]

   展开重组得，

   \[|f| = \sum_{v \in V} \left(f(s,v)+\sum_{v \in {S - \{s\}}}f(v,u) \right ) - \sum_{v \in V}\left(f(v,s) + \sum_{v \in S - \{s\}} f(u,v) \right) \]

   惊奇地发现，

   \[|f| = \sum_{v \in V}\sum_{u \in S}f(u,v) - \sum_{v \in V}\sum_{u \in S}f(v,u) \]

   (跟 \(f(S,T)\) 已经有点像了，集合不同)
   因为 \(V = S \cup T\)，且有 \(S \cap T = \varnothing\)，可将针对 \(V\) 的求和，分解为针对 \(S\) 和 \(T\) 的求和，得到

   \[|f| = \sum_{u \in S} \left( \sum_{v \in S}f(u,v) + \sum_{v \in T}f(u,v) \right) - \sum_{u \in S} \left( \sum_{v \in S}f(v,u) + \sum_{v \in T}f(v,u) \right) \]

   "观察到"，

   \[|f| = \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T}f(v,u) + \left( \sum_{u \in S}\sum_{v \in S}f(u,v) - \sum_{u \in S}\sum_{v \in S}f(v,u) \right ) \]

   括号内，\(u,v\) 对称，值为 \(0\)。
   我们终于得到，

   \[|f| = \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T}f(v,u) = f(S,T) \]

   感性地理解，根据流量守恒和流网络的连通性( \(\forall u \in V, \exist s \rightarrow u \rightarrow t\) )，无论在哪里划分，从 \(S\) 到 \(T\) 的净流量总是恒定的，且等于 \(|f|\)。
   
   

2. 流网络 \(G\) 中任意的 \(|f|\) 不能超过 \(G\) 任意的 \(c(S,T)\)。
   wuhupai注：数学推导较好理解，也可以感性理解
   \(\triangle\)证明如下：
   设 \(f\) 为任意流，\((S,T)\) 为任意切割。

   \[|f| = f(S,T) = \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T}f(v,u) \]
   \[|f| \le \sum_{u \in S}\sum_{v \in T}f(u,v) \]
   \[\sum_{u \in S}\sum_{v \in T}f(u,v)-\sum_{u \in S}\sum_{v \in T}f(v,u) \le \sum_{u \in S}\sum_{v \in T}f(u,v) \]
   \[\sum_{u \in S}\sum_{v \in T}f(u,v) \le \sum_{u \in S}\sum_{v \in T}f(u,v) + \sum_{u \in S}\sum_{v \in T}f(v,u) \]
   \[\sum_{u \in S}\sum_{v \in T}f(u,v) \le \sum_{u \in S}\sum_{v \in T}c(u,v) \]
   \[|f| \le \sum_{u \in S}\sum_{v \in T}f(u,v) \le \sum_{u \in S}\sum_{v \in T}c(u,v) = c(S,T) \]

   最直观的结论是，最大流 \(\le\) 最小切割
   
   

3. 最大流最小切割定理
   设 \(f\) 为流网络 \(G = (V, E)\) 中的一个流，则有以下 \(3\) 个条件等价：
   \(a\). \(f\) 是 \(G\) 的一个最大流
   \(b\). 残存网络 \(G_f\) 不包括任何增广路径
   \(c\). \(|f| = c(S,T)\)，其中 \((S,T)\) 是 \(G\) 的某个切割
   \(\triangle\)证明如下：
   \(a \Rightarrow b\)，显然
   \(b \Rightarrow c\)，假定 \(G_f\) 不包含任何增广路径 \(p\)，即任意的 \(c_f(p) = 0\)，在这里认为是"不存在" \(s\) 到 \(t\) 的路径。定义 \(S = \{v \in V : 在 G_f 中存在一条路径s \rightarrow v\}, T = V - S\)。显然有 \(s \in S, t \in T\)，所以 \((S,T)\) 是 \(G\) 的一个切割。
   设有 \(u \in S, v \in T\)，

   1. 若有 \((u,v) \in E\)，则必有 \(f(u,v) = c(u,v)\)，否则根据残存网络定义，\(c_f(u,v) = c(u,v) - f(u,v) > 0\)，会有 \((u,v) \in E_f\)，与条件 \(b\) 矛盾。
   2. 若有 \((v,u) \in E\)，则必有 \(f(v,u) = 0\)，否则根据残存网络定义，\(c_f(u,v) = f(v,u) > 0\)，会有 \((u,v) \in E_f\)，与条件 \(b\) 矛盾。
   3. 若有 \((u,v) \notin E,(v,u) \notin E\)，则 \(f(u,v) = f(v,u) = c_f(u,v) = 0\)，可行。

   综上，可以得到，

   \[|f| = f(S,T) = \sum_{u \in S}\sum_{v \in T}f(u,v) - \sum_{u \in S}\sum_{v \in T}f(v,u) = \sum_{u \in S}\sum_{v \in T}c(u,v) - \sum_{u \in S}\sum_{v \in T}0 = c(S,T) \]

   此时，\(|f|\) 最大，\(c(S,T)\) 最小，即最大流 \(=\) 最小切割。

   \(c \Rightarrow a\), 由证明 \(2\)，\(|f| \le c(S,T)\)，则此时 \(f\) 便为最大流。
   wuhupai注:我们取出一个最大流和最小割，考虑这个最大流的残存网络，因为这是不存在增广路径，这时从S点出发能到达的集合和从T点出发能到达的点的集合就构成了一个割，所以流的集合和割的集合都有了这个元素，因为大于等于的关系，那么这个最大流就是最小割

3. Ford-Fulkerson思想：

1. 步骤
   \(|f| = 0\) \(\rightarrow\) 构建残存网络 \(G_f\) \(\rightarrow\) 寻找增广路径 \(p\) \(\rightarrow\) \(|f| = |f| + c_f(p)\) \(\rightarrow\) 直至 \(G_f\) 不存在 \(p\) 时结束。
   
   
2. 随堂思考
   为何最后找到的 \(|f|\) 是最大流，尝试用之前讲过的知识解释。

最大流最小切割定理的三个等价条件。

4. 多种实现方式：

本质都是 \(\texttt{Ford-Fulkerson}\) 思想，只不过实现效率不同。

wuhhupai注:new_hope 几乎没讲反向边的作用，这里来讲一下

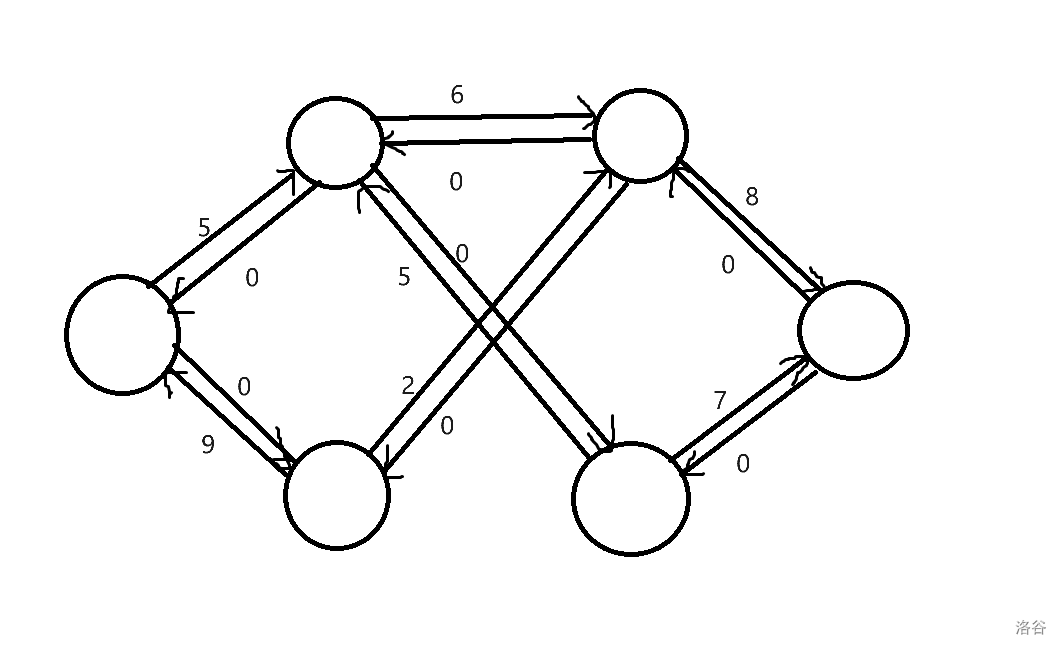
（画错了，懒）
这是一个我也不知道是什么的东西，但建图建出来就是这样，因该是流网络和残存网络的叠加体，边权为0的边是流网络，正的是残存网络（因为什么都没有操作）
比如说我找到了两条增广路径（只是演示）

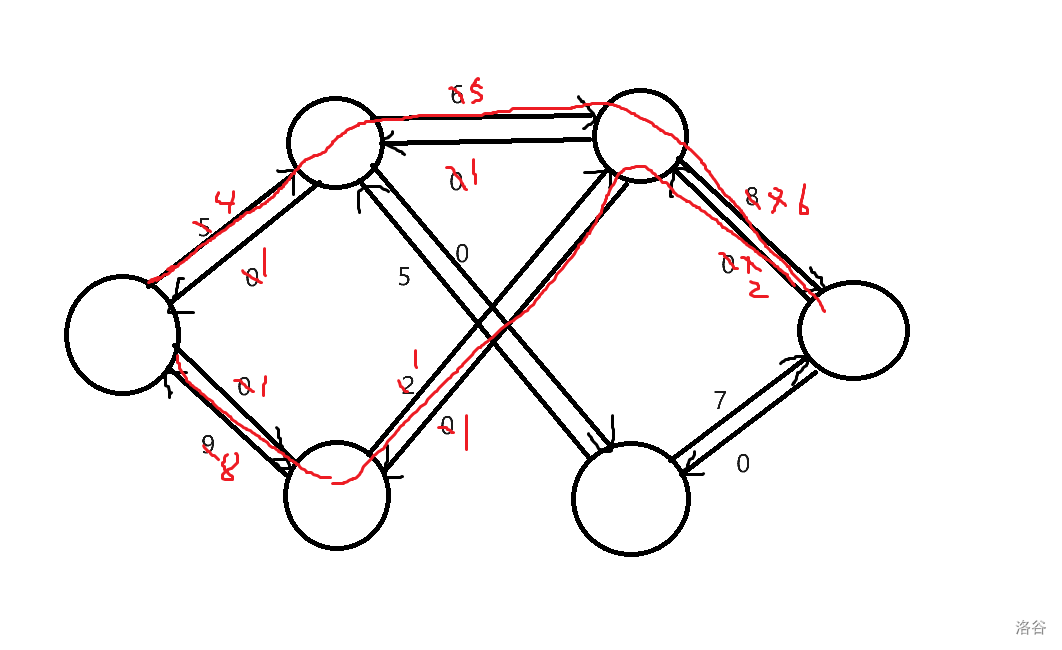
那么我要找下一条增广路

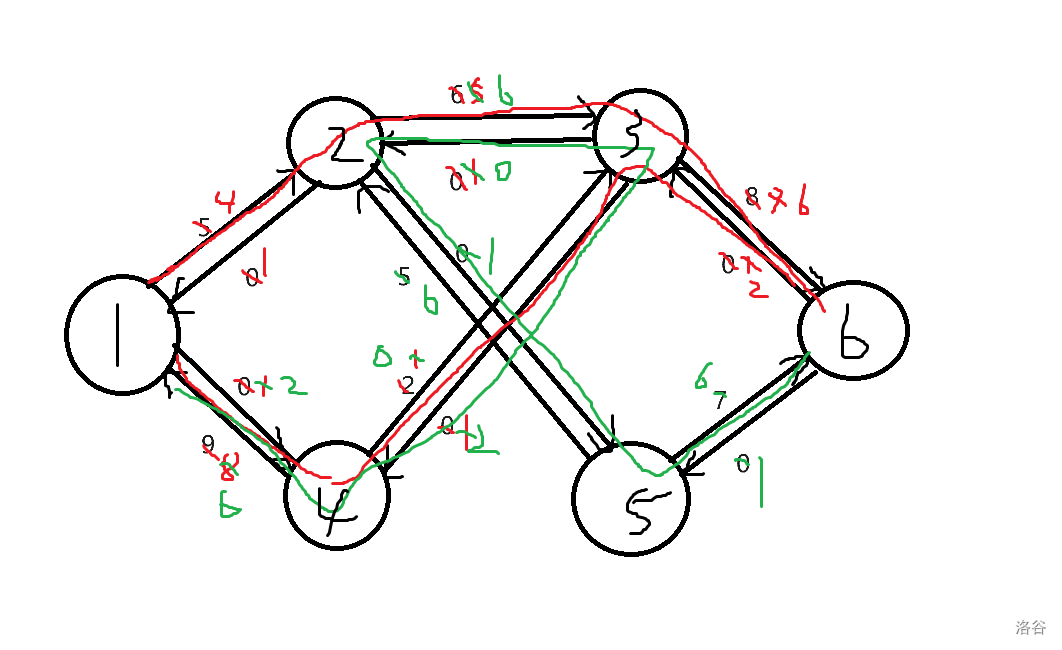
(给节点标了个号)
此时我们发现原来1-2-3-6和1-4-3-6的增广路变成了1-4-3-6和1-2-5-6达到了找增广路的目的，所以这是对的，感性理解并且会用就行
————————————————————————————————————————————————

1. \(\texttt{Edmonds−Karp}\) 算法
   • 主要步骤：每次 bfs 搜一遍残存网络，找到一条增广路，更新最大流与残存网络。
   • 时间复杂度：\(O(nm^2)\) (\(n\) 点数，\(m\) 边数)
2. \(\texttt{Dinic}\) 算法
   • 主要步骤：每次 bfs 搜一遍残存网络，建分层图，找到多条可能的增广路，再 dfs 找到增广路的残存容量，更新最大流与残存网络。
   • 时间复杂度：\(O(n^2m)\) (\(n\) 点数，\(m\) 边数)

// Edmonds−Karp 核心部分
int bfs() {  
    for(int i = 1; i <= n; i ++) vis[i] = 0;
    queue<int> q;
    q.push(s);
    vis[s] = 1;
    dis[s] = 2005020600;
    while(!q.empty()) {
        int x = q.front();
        q.pop();
        for(int i = head[x]; i; i = e[i].net) {
            if(e[i].val == 0) continue;    
            int v = e[i].to;
            if(vis[v] == 1) continue; 
            dis[v] = min(dis[x], e[i].val);
            pre[v] = i;//记录路径
            q.push(v);
            vis[v] = 1;
            if(v == t) return 1;
        }
    }
    return 0;
} //寻找增广路
void update() {   
    int x = t;
    while(x != s) {
        int v = pre[x];
        e[v].val -= dis[t];
        e[v^1].val += dis[t];
        x = e[v^1].to;
    }
    ans+=dis[t];   
} //构建残存网络

//Dinic 核心部分
bool bfs() {
    queue<int> q; memset(dep,0,sizeof(dep)); 
    q.push(s), dep[s] = 1;
    while(!q.empty()) {
        int fr = q.front(); q.pop();
        for(int i = head[fr]; i; i = edge[i].ne) {
            int ed = edge[i].v, w = edge[i].c;
            if(!dep[ed] && w) {
                dep[ed] = dep[fr] + 1;
                if(ed == t) return true;
                q.push(ed);
            }
        }
    } 
    return false;
} // 分层图找增广路
int dfs(int u,int minf) {
    if(u == t) return minf;
    int sum = 0;
    for(int i = head[u]; i; i = edge[i].ne) {
        int ed = edge[i].v, w = edge[i].c;
        if(dep[ed] == dep[u] + 1 && w) {
            int f = dfs(ed,min(minf,w));
            edge[i].c -= f;
            edge[i^1].c += f;
            minf -= f;
            sum += f;
            if(minf == 0) break;
        }
    }
    if(sum == 0) dep[u] = 0;
    return sum;
} // 构建残存网络，更新最大流

视频模拟网络流

三、好多网络流题

“网络流的题目难在建模。”——Rayleigh.
“【】”——wuhupai
“网络流解决的问题很像NPC”——DXqwq

1. 最大权闭合子图问题

1. 前置知识

闭合子图：对于有向图 \(G\)，存在点集 \(V\)，满足点集内所有的点，他们的出边指向的点都是 \(V\) 内的点，将有向边添加上，就是一个子图。（可以有入边）
wuhupai注:

简单割：在一个割中,如果连接两个集合的边都是源点或者汇点的邻边,那么这个割被称为简单割。

最大权闭合子图即求解上述子图中点权和最大的子图。

如何将闭合子图变成流网络？

2. 步骤：

建一个源点，和一个汇点；
\(s\) 连向权值为正的点，流量赋为点权；
权值为负的点向 \(t\) 连一条边，流量赋为点权的绝对值；
点与点之间的有向边不变，流量赋为正无穷。

原理？
//这个v1假设成了闭合子图

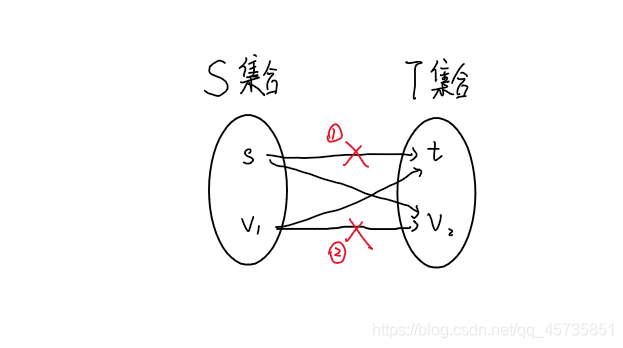
割的所有情况共有四种（ \(S\) 集合到 \(T\) 集合共四种情况），其中有两种情况不存在，第①种情况不存在是因为我们在建图时就不会建 \(s\) 到 \(t\) 的边，第②种情况不存在是根据闭合子图的定理，从 \(v_1\) 出发的点一定会回到 \(v_1\)，不会到 \(v_2\)。

为啥割中没有 \(s \rightarrow v_1\) 和 \(v_2 \rightarrow t\) 的边，假设有，那么 \(S,T\) 联通

3. 数学推导：

设简单割 \((S,T)\)，闭合子图 \(G_1 = (V_1, E_1)\)，原图 \(G\) 的闭合子图的补图 \(G_2 = (V_2, E_2)\)

由图知，割中不存在 \(v_1 \rightarrow v_2\)，和 \(s \rightarrow t\) 的边，只有 \(v_1 \rightarrow t\) 和 \(s \rightarrow v_2\) 的边，所以可以得到该割的容量 \(c(S,T)\) 为：

\[c(S, T) = c(V_1, \{t\}) + c(V_2, \{s\}) = (\sum_{v \in V_1^{-}} -W_v) + \sum_{v \in V_2^{+}} W_v \]

闭合子图的权值

\[W = \sum_{v \in V_1^{+}} W_v + \sum_{v \in V_1^{-}} W_v = \sum_{v \in V_1^{+}} W_v - (\sum_{v \in V_1^{-}} -W_v) \]

两个量相加有(加括号的式子抵消)，

\[W + c(S,T) = \sum_{v \in V_2^{+}} W_v + \sum_{v \in V_1^{+}} W_v = \sum_{v \in V^{+}} W_v \]

最后得到，

\[W = \sum_{v \in V^{+}} W_v - c(S,T) \]

在左项恒定的情况下，若要得到最大的 \(W\)，则仅需求得最小的 \(c(S,T)\)，而最大流最小切割定理告诉我们，这可以转化为最大流求得。

wuhupai注:这里我们求的是 \(v1\) 这个闭合子图的权值之和。

看懂数学推导还是比较困难的，我们 \(s\) 每连出去一条边，就代表一个正权点没有选，\(t\) 每连出去一条边，就代表选了一个负权点，然后就好了

有啥用呢？

CF311E

为啥是网络流，怎么与最大权闭合子图建立联系？

分析题目，发现 \(0/1\) 修改比较麻烦，先假设所有的点都被改为 \(1\)。当前的答案是：所有 \(1\) 要求的 \(w\) 之和 \(-\) 所有修改为 \(0\) 点的 \(v\) 之和 \(-\) \(g\) 乘上 \(0\) 要求中要求倒给的个数。

现在，在上述的假设下，如果要满足一个 \(0\) 要求，那么该要求所有相关的点都必须进行修改，如果一个点进行了修改，那么该点所有有关的 \(1\) 要求都不满足。

这和之前 闭合子图中一个点被选择了则后继必须被选择 这一性质是一样的，我们考虑建图。

怎么建图？

注意接下来的分析还是基于所有点都被改为 \(1\) 的题设。

原先为 \(0\) 的点，因为之前已经被修改过一次，如果修改该点就相当于反悔，会产生 \(v\) 的贡献。

原先为 \(1\) 的点，如果修改该点，会产生 \(-v\) 的贡献。

对于每个 \(0\) 要求，如果将该要求改为满足，那么对答案会产生 \(w\) 贡献，如果该节点还要倒贴，一共会产生 \(w+g\) 贡献，将贡献作为点的权值，而且所有与它相关的点都必须选，于是连该要求到所有有关的点的边(出边)。

对于每个 \(1\) 要求，如果将该要求改为不满足，那么对答案会产生 \(-w\) 贡献，如果还要倒贴，一共会产生 \(-w-g\) 贡献，将贡献作为点的权值，而且所有与它相关的点一个被修改该要求也会不满足，所以连所有有关的点到该要求的边(入边)。

接着我们按照前面所讲的步骤，利用网络流求解最大权闭合子图问题。

补充：最终构造的流网络中，贡献为所有的所有 \(0\) 要求的 \(w\) 之和 \(+\) 所有 \(0\) 点的修改代价 \(+\) \(g\) 乘上 \(0\) 要求中要求倒给的个数 \(-\) 最小割，加上题设的答案，最终答案为 \(\sum w - MinCut\)

• 下面是集训extra

[P3749]

我们将区间变成一个上三角，然后如果我们选了一个点，那么左下角的点都要选。

然后这个就是最大权闭合子图问题了，当然还有点的贡献。如果我们闭合子图里面包含了一个代号，那么就直接 \(mx^{2}\)，如果选了一个寿司，那么久再加上 \(c\)，然后就做完了。

[ARC161F]

有点神。问题转化为，是否存在一个点集的导出子图比原图更稠密。我们建图，一条边的代价是 \(-1\)，一个点的代价是 \(+D\)，然后选一条边必须选两个点，然后就变成了最大权闭合子图问题了。如果答案大于 0，那么必然合法，如果答案等于 0，则要考虑是否我们求出来的图是否为原图。怎么判定呢？
发现一种很妙的解法，我们不是要特意搞出来个子图满足条件吗？那么我们是求最小割，那么我们只要让原图中的边能被割掉即可，那么我们只要将边的容量设为1-eps即可，容易理解正确性。

2. 图上问题

建模方式：每个点拆成入点和出点转成二分图匹配。

例：最小路径覆盖问题
给定一张图，求最少能用多少条边不相交的路径覆盖所有点。

考虑将每个点 \(u\) 拆成入点 \(in_u\) 和出点 \(out_u\)，那么对于一条边 \((u,v)\)，它的作用就是将 \(in_u\) 所属的路径与 \(out_u\) 所属的路径合并，使得路径数 \(-1\)。

由于路径不能相交，所以每个 \(in_u\) 和 \(out_u\) 只能合并一次，那么就相当于初始时有 \(n\) 条路径，我们希望用若干条边减去最多的路径数。
该数目就等于以 \(in_u\)，\(out_u\) 为点，以 \((in_u,out_u)\) 为边的二分图最大匹配。
于是有：最小路径覆盖数 = 总点数 - 最大匹配数。

LuoGu P2764

思考：用匈牙利算法和最大流算法分别如何实现路径输出

匈牙利算法：利用数组 \(match[]\) 递归输出。

bool find(int x) {
    for(int it : g[x]) {
        if(vis[it]) continue;
        vis[it] = 1;
        if(!match[it] || find(match[it]))
            match[it] = x; return true;
    }
    return false;
}
void rec(int u) {
    r[t].push_back(u);
    for(int it : g[u])
        if(match[it] == u) rec(it);
    return;
}
void solve() {
    int ct = 0;
    for(int i = 1; i <= n; i ++) {
        memset(vis, 0, sizeof(vis));
        ct += find(i);
    }
    for(int i = 1; i <= n; i ++)
        if(!match[i]) t ++, rec(i);
    for(int i = 1; i <= t; i ++) {
        for(int it : r[i]) cout << it << " ";
        cout << "\n";
    }
    cout << n - ct;
}

最大流算法：在残存网络中寻找满流的边。

留给大家发挥

图上问题其实都与之前二分图的解法相同，不再过多介绍。

3. 最小割问题

广义地来说，最大权闭合子图问题可归类于最小割问题，但发现答案具有闭合子图的性质较难（对于讲者来说），最小割通常为“选择”问题。

一类“选择”问题：选择若干个物品使得收益之和最大（即没选的物品收益之和最小），满足约束。

建模方式：
源点向每个物品连边，边权为收益，割掉该边表示不选该物品；
每个物品向汇点连边，边权为代价，割掉该边表示选该物品；
中间的连边视题目约束而定。
最大值：\(Ans = \sum val - MinCut\)

这里不太好理解的地方在于，\(-MinCut\) 实际上是对于答案的贡献，比如一个物品 \((val_i,w_i)\)，其价值 \(val\) 已被统计到 \(\sum val\) 中，所以有选该物品则需带上代价 \(w_i\)，不选该物品要撤销价值 \(v_i\)。

4.网络流24题+杂题

飞行员配对方案问题

首先我们将外籍飞行员连向源点，英国飞行员连向汇点，边权均为 1，然后对于给定的关系，边权也为 1。然后我们就求出了一次能派出的最多飞机数量，然后考虑怎么输出方案。如果一个外籍飞行员和英国飞行员的流量为 1，那么这两个就配合，输出即可。

试题库问题

首先看这道题，是一个最大流问题。考虑最大流是什么，因为所有试卷都要被包含进去，所以最大流就是试卷的数量。然后每个类型连汇点，边权无限然后试卷连类型，边权为 1，然后源点连试卷，边权为 1，然后按照残量网络输出路径即可。

圆桌问题

看这道题，是个最大流问题。考虑最大流是什么，因为每个人都要入座，所以最大流就是人。然后公司连每个餐桌，边权为 1。源点连每个公司，边权为公司人数。餐桌连汇点，边权为能容纳的元素，然后按照残量网络输出路径即可。

分配问题

看这道题，是个费用流问题。考虑最大流是什么。因为每个人都要干活，所以最大流就是人。然后源点连人，人连任务，跑下费用流就行了。

运输问题

看到货物供需平衡其实就可以往网络流这方面想了。看这道题，是个费用流问题。考虑最大流是什么。因为供需平衡，所以最大流就是货物。跑下费用流就行了。

餐巾计划问题

看这道题，是个费用流问题。考虑最大流是什么。因为要保证每天的餐巾都供的上，那么流就是每天的餐巾。然后先拆个点，将点拆为白天和晚上。首先这个送洗操作可以将一天的晚上连到后面的白天做到。原点向白天流的是新买的，源点向晚上流的是当天一共有多少餐巾，然后这些餐巾回流到下一天晚上或新一天的早上。然后白天连上汇点。这个建图还是比较独特的，但按照上面的步骤思考还是可以做出来的。在最后跑下费用流即可。

这样可以刻画的限制一般形如：如果一个元素被划入集合 \(A\)，另一个元素被划入集合
\(B\)及之后，产生的代价。这里需要保证非负性。

happiness

反正不看题解写不出来。考虑要将一些元素划入两个集合，并产生一些代价。在一些元素共同在一个集合时，会产生一些代价。我们通常是这样做的:

使用最小割，考虑将尽可能小的流割掉。
和左边集合相连，代表选文，和右边集合相连，代表选理，中间小小的是共同在一个集合的代价。
如果两个人都选文，为了不连通，那么割掉的边就会是 \(w_{4},w_{5},w_{6}\)，如果有一条保留，那么就矛盾。
如果一个人选文，一个人选理，为了不连通，那么割掉的边就会是 \(w_{2},w_{3},w_{4},w_{5}\)，如果有一条保留，那么就矛盾。
其他同理。

Luogu P1646

如果我们暂且不考虑第 \(3 \sim 6\) 个矩阵，怎么做？

非常简单，对于一个人拆成两个点，\(s\) 连向 \(u_1\) 代表选理科，\(u_2\) 连向 \(t\) 代表选文科，\(u_1\) 连向 \(u_2\) ，容量正无穷，根据上述套路求解即可。

考虑如何体现 \((i,j)\) 同时/不同时选文科的贡献?

首先，如果同时选文科肯定会有新增的贡献，根据得到答案的套路，我们肯定是要新增一个节点并与 \(s\) 相连。

\((i,j)\) 不同时选文科时，假设有 \(s \rightarrow i\) 而没有 \(s \rightarrow j\)，同时也有 \(j \rightarrow t\) 而没有 \(i \rightarrow t\)。

\((i,j)\) 同时选文科时，有 \(s \rightarrow i\) 和 \(s \rightarrow j\)，同时没有 \(j \rightarrow t\) 和 \(i \rightarrow t\)。

充分发扬人类智慧，新增一个节点 \(p\)，从 \(s\) 连一条容量为都选择文科的贡献到 \(p\)，从 \(p\) 连向 \(i,j\) 的边容量为正无穷。【画图说明】(理科操作同理)

[佚名]

网络流难以刻画一个点的颜色数这种东西，考虑转化。我们发现每种颜色的球是一样的，而且只有一个能产生贡献，那么我们规定一个球能产生贡献，其他球不能产生贡献，这样我们的颜色数就是黑球的个数了。然后考虑刻画这个交换。我们从上面的思路很容易想到将流量看作黑球个数，容量看作球的总数，那么我们的交换一定是白球和黑球交换，否则没有意义，那么我们这样建图。我们将箱子拆成入点和出点，那么我们的交换就是将一个的入点连到另外一个点的入点，然后就可以了？但是我们交换有先后顺序啊，那还是正常建边，差不多了。就是一层一层这样了

5.网格染色型

方格取数问题

像这种有限制的方格问题我们基本都可以用网络流做，具体的就是对网格进行黑白染色，但这个染色不是随便染的，这个染色要保证从一个格子走到另一个格子时，两个格子异色。对于这道题，我们先假设所有点都可以选，然后减去那些不能选的格子。我们就是这样染色

然后相邻的黑白格子连边

然后我们会发现左边就是黑色格子，右边就是白色格子。点（后续会进行拆店）的容量就是该点的权值。我们要求一个最小割，就是将一些点割断，使得没有点之间互相连通，这里还用到了最小割的性质，割去的边必定是满流边（要么还是有联通，要么不是最小），然后这题就做完了

骑士共存问题

与上题相同的黑白染色方法

王者之剑

首先看题意，如果发现我们停留一秒，那么会发现一个很蠢的事。比如我们先在起点拿宝石，然后四周消失，然后停一秒，然后到四周，取的是 0，因为这是偶数秒，那么四周又会消失，这样就不能取到其他东西了。所以这就是停留奇数秒的情况，这是肯定没有听偶数秒优的，所以这个就不用停。所以这题就变成了方格取数问题。

方格取数加强版

黑白染色，然后相邻各自之间连边，因为可以走 \(k\) 次，那边权容量为 \(k\),权值为 \(w\)。但这里经过一次权值就会消失，所以我们可以连一条权值为 \(w\) 容量为 1 的边，和权值为 0，容量为 \(k-1\)。后然后跑一边费用流即可。

长脖子鹿放置

发现传统的黑白染色方法不再适用。于是我们可以随机找一个点，用你智慧的大脑跑一边模拟。就是钦定这个点是黑色，那么能到达的点就是白色。如果还有没有染色的点，那么就重复这个操作。或者还有一种方法，因为我们每次都向上或向下奇数行，所以我们可以对相邻行染色。又有一种染色方法，是非常神奇的。我们将图按照传统方法染色，然后将黑点和白点分开形成一张新图，发现不会有跨图的边，然后再每张图内部跑骑士共存问题就行了。

水晶

直接染色，然后就可以了

老C的方块

感觉比 happiness 简单 qwq
看到是网格，想到染色。因为限制在四个格子内进行，所以考虑染成四种颜色，然后稍微跑下网络流就可以了。

线性规划

没学过，先咕着，但是听懂了一道题

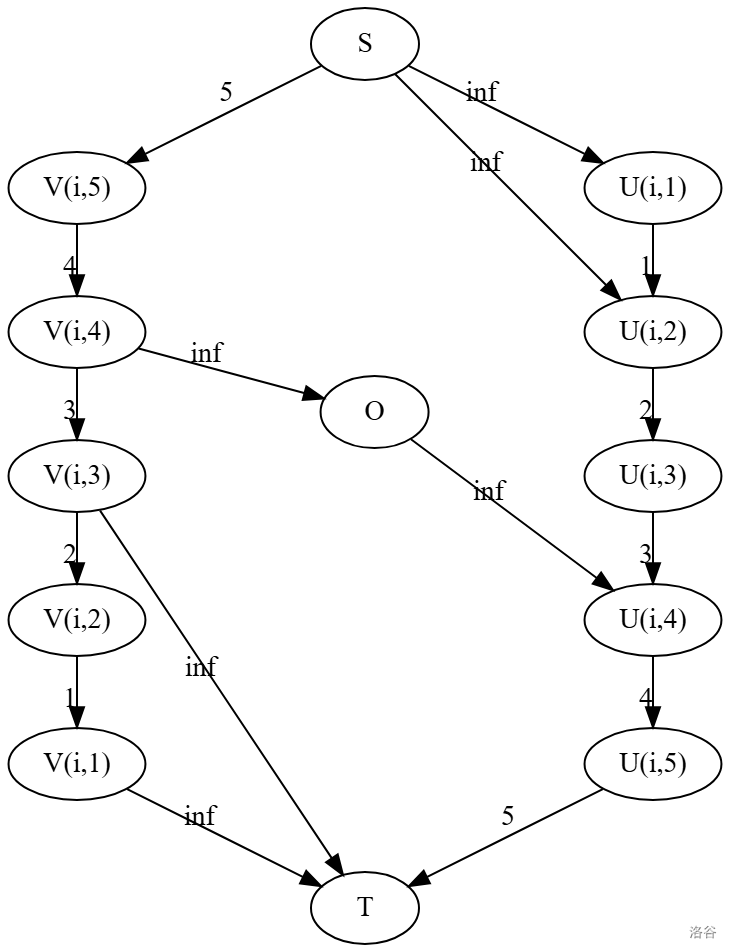
志愿者招募

这题看起来十分困难，实则十分困难。考虑如何用网络流刻画这些条件。首先每天必须得有 \(a_{i}\) 个人，那么我们希望流进这条边至少有 \(a_{i}\) 的流量，同时流过还有费用，每类人可以工作一段天数，我们可以这样建模。

我们发现如果这样，那么就可以解决这个问题了。平的边代表天，弯的边代表人。

费用流

最小(大)费用最大流：在满足最大流的前提下使得所花费用最少(多)。
实现：寻找增广路时使用SPFA处理。
方式：基于 \(\texttt{EK}\) 或 \(\texttt{Dinic}\)。

Luogu P3381 【模板】最小费用最大流

板题，这里是基于 \(\texttt{EK}\) 的代码。(似乎费用流中 \(\texttt{EK}\) 用得多些)

bool spfa()
{
    clear();
    queue<int> q;
    q.push(s); vis[s] = 1; mxcf[s] = inf; dis[s] = 0;
    while(q.size())
    {
        int fr = q.front(); 
        q.pop(); vis[fr] = 0;
        for(int i = hd[fr]; i; i = e[i].nx) 
        {
            int v = e[i].v, C = e[i].C, F = e[i].F;
            if(C && dis[v] > dis[fr] + F) 
            {
                dis[v] = dis[fr] + F;
                if(!vis[v]) { q.push(v); vis[v] = 1; }
                mxcf[v] = min(mxcf[fr], C);
                pre[v] = i;
            }
        }
    }
    return mxcf[t] > 0;
}
void update()
{
    int v = t;
    do {
        int id = pre[v];
        e[id].C -= mxcf[t], e[id ^ 1].C += mxcf[t];
        v = e[id ^ 1].v;
    } while(v != s);
    mxFl += mxcf[t];
    mnFe += mxcf[t] * dis[t];
}   

LuoGu P6577 【模板】二分图最大权完美匹配

理解透后应该也可以写了。

CF277E Binary Tree on Plane

约束——二叉树的性质：“树”和“二叉”的性质。

想清楚上面这个问题大概就好做了。
树的性质：一个节点必须是一个节点的儿子。
二叉树的性质：一个节点最多有两个儿子。

建图？判断无解？

可能会有同学想到拆点限流，但这道题对于一个点有双重限制，所以这里使用拆点。
我们根据这两个约束对一个节点拆为 \(u_{fa}\) 和 \(u_{son}\) 两个点，\(s\) 向 \(u_{fa}\) 连容量为 \(2\) 的边，代价 \(0\)，代表可最多容纳两个儿子，\(u_{son}\) 向 \(t\) 连容量为 \(1\) 的边，代价 \(0\)，代表最多成为一个节点的儿子。\(u_{fa}\) 向 \(v_{son}\) 连容量 \(1\)，代价距离的边。最终一条 \(s \rightarrow u_{fa} \rightarrow v_{son} \rightarrow t\) 的路径代表 \(u\) 成为了 \(v\) 的父亲。

\(\triangle\) 另一方面，最大流中很少出现带小数的流，所以考虑将距离作为代价。

LuoGu P4066

路径不相交问题经典思路：若有两条路径相交，则可交换两人身份，具体在这道题也有体现，\(\text{Dong Shu Cheng}\) 的一篇题解中也有涉及。（所以本质上“不相交”只是用来迷惑的）

建图？

应该能想到，对于每个点的限制拆成 （入点，出点，边） 考虑，连边细节留给大家，最后跑最大费用最大流即可。

Tips：连边需要优化。（最大流复杂度）

[ARC137E]

详见lyc的题解，非常好的题解，说的天真想法我基本都想过了。下面基本就是抄的，但有自己理解。

考虑费用流算法，这个算法的基础是最大流条件下的最小费用，这题的关键在于费用容易处理，但是流量是什么呢？

天真的想法是直接把面包当做流量，面包师向它做的面包连边。这样做的问题在于：

1. 不好处理雇佣面包师的代价。
2. 制作面包最多的方案是不一定是利润最大的。

于是我们可以用钦定最大流的技巧，建一个最大流一定是 \(\infin\) 的网络，这样就不用考虑的流量的问题了。

那怎么建图呢？详见P3980 NOI 2008 志愿者招募

我们仍然可以把面包当作流量，钦定最大流为 \(\infin\)。我们可以先假设我们能够得到所有面包的利润，即先让 \(w=d\sum a_i\)。我们让图上的最小代价表示的是与 \(w\) 相比损失的代价。于是关于面包的建图如下：第 \(i\) 个点表示第 \(i\) 天，\(i\to i+1\) 连两条边：一条容量为 \(a_i\)，代价为 \(d\)，走这条的边就代表不做面包，所以会损失 \(d\) 的代价；另一条容量为 \(\infin-a_i\)，代价为 0，走这条边就代表实际上没有面包了（这条边存在的意义就是保证最大流为 \(\infin\)）。

这样建出来的图满足：最大流为 \(\infin\)，最小费用为 \(w\)。

关于这个图的意义，我们要保证每天都做了 \(\infin\) 个面包，那么既然每天代价为0的面包只能做 \(\infin-a_i\) 个，那么自然就会去做花钱的面包了

随后考虑加入面包师对网络的影响，\((l,r,c)\) 可以建成图上 \(l\to r+1\) 的一条容量为 1，代价为 \(c\) 的边。这样的含义是有一位面包师可以在 \([l,r]\) 的时间内每天提供一个面包。这么建图的正确性：连上这条边之后，\(\forall l\leqslant i\leqslant r\)，\(i\rightarrow i+1\) 的那条代价为 \(d\) 的边的流量可以减少 1，最多减少 \(a_i\) 次，就相当于第 \(i\) 天每个面包师可以做一个面包，所有面包师最多做 \(a_i\) 个。

于是我们可以得到一个算上负权边共 \(2(2n+m)\) 条边的网络，在这张图上跑 EK 就可以得到答案。

考虑到每次 EK 的增广路有如下三种情况：

1. 全走费用为 0 的边，必然是第一次增广的情况
2. 包含一条面包师的边，最多有 \(m\) 次增广会包含此情况

注:如果有一条路径经过的全都是老的面包师（也就是全部都没有），那么这个肯定是没啥用的。

3. 其它情况，必然包含至少一条流满的 \(i\to i+1\) 的容量为 \(a_i\)，代价为 \(d\) 的边，不然根据增广路的性质，可以增大流量

注:根据我们EK代码理解即可

于是增广轮数最多是 \(2m+1\)，时间复杂度也是 \(O(nm\log n)\)。

然后稍微优化一下即可

[CF2038H]

还是神仙题？
仔细观察，我们在第一回合会知道执政党的票数，考虑观察接下来执政党的票数情况，分讨，比较好理解。

1. 若 \(p_{i+1}<p_{i}\)，那么说明在 \(i\) 回合 \(val_{p_{i+1}}+1=val_{p_{i}}\)，而在 \(i+1\) 回合，\(val_{p_{i+1}}=val_{p_{i}}\)
2. 若 \(p_{i+1}=p_{i}\)，由于不能支持自己，那么 \(val_{p_{i+1}}=val_{p_{i}}\)
3. 若 \(p_{i+1}<p_{i}\)，那么说明在 \(i\) 回合 \(val_{p_{i+1}}=val_{p_{i}}\)，而在 \(i+1\) 回合，\(val_{p_{i+1}}=val_{p_{i}}+1\)
   然后我们保证其他参政党随便搞一下这个限制就刻画完全了。
   然后我们设一些点代表每个回合，然后从 \(S\) 连边到 \(u\)，容量为1，em，我们得构造一下保证这条边流满的，然后我们还有 \(m*n\) 个党派在每回合的选票情况。由于我们会限定一些流量的流通，然后对于参政党，我们有的是流量，可以限制票数多和少。我们只要不乱流，那么每天的选票就自然会继承到下一天，然后是不是就好了？我们有限制！也就是限制执政党的票数，怎么保证这个被流满呢？我们只要搞容量为当天票数并且费用为 \(-inf\) 的边就可以了！因为我们肯定有合法的流吧，然后因为我们知道了要流多少，所以直接在答案里减即可

[AGC031E]

看看 Hint，只有一个维度的矩形限制怎么做？
dp，但是 trivial，考虑用网络流怎么做。选的宝石肯定就是流量了，我们前几行行作为一个节点，然后流过来，然后宝石就是从外面流进来，然后就做完了。
只有左侧和上侧怎么做？
不会。
不思考 hint了。考虑枚举偷了几个宝石，然后就变成恰好偷 \(k\) 个宝石的代价，然后我们四维的限制就变成了二维。然后我们就可以假设宝石已经排好序了，所以每个宝石坐标还有范围？
考虑如何求这个范围，如果一个点的 \(id<b_{i}\)，那么对横坐标就会有一个限制。然后这个限制区间应该是随着 \(id\) 增大，左端点单调不降，右端点单调不增的。此时是不是可以把宝石横坐标的相对大小这个限制抛掉。只要所有点都满足这个关系，那么相对大小也就不重要了。
两维在网络流中有一个很经典的东西，就是 \(S\) 连横坐标，\(T\) 连纵坐标。那么我们将那个点连向个区间，然后横纵坐标连边连到汇点，这里就有费用了，前面都没有费用的。

[CF2109F]

注意读题。
我们首先可以求出来 M 的代价吧，也就是二分答案bfs。

看看 hint，如果不改变怎么做？首先用网络流刻画最小值很简单，就是一条路径流下去就可以了。注意到允许操作的次数为 \(1e6\)，我们不可能把这个扔到图里面。

我们还是二分答案。考虑什么样的情况会合法，那就是一条隔开起点和终点的八连通路径，其中路径上的所有格子都大于 \(mid\)，这样我们的 F 走下去肯定会经过其中的一个格子。考虑如何使用这个东西刻画。首先这个特别像最小割对吧，我们的一个最大流就对应着一个最小割，那么我们将每个格子都拆成入点和出点，然后格子四联通连边，这个最小割代表什么，那么就是八联通的这个路径了。我们如果一个格子 \(\ge mid\) 了，那么我们就直接不给这个连边了，否则我们格子的容量就是 \(mid-a[i]\)，考虑怎么刻画这个黑格子白格子的方案，那么把白格子变成不能割，也就是容量特别大就可以了。为啥题解网络流都没用啊。em其实这是一个多源汇最短路，也就是从上边界到下边界找出一条路径，使得上面最小，很显然。聪明的小朋友会想到 [P7916 交通规划]
考虑加回 M 的限制。
先分讨：

• 若 \(mid\le M\) 那么答案肯定不会改变
• 否则直接开始深度思考
  因为我们的起点不同，所以我们挑的路径得尽量避开我们的墙。感性告诉我们我们最优的路径Q是唯一的。对于两条不同的路径 \(Q_1\) 和 \(Q_2\)，他们的相邻交点会产生多边形，而交点将多边形的边分为两段，选择其中一段可以使得相较于另一段， \(P\) 的选择空间多出了整个多边形，则每个多边形选择更优的一段可以得出更优的一条路径。嗯，非常有道理，然后我们把这些点也变成不能选，然后就做完了。
  网络流真的要关心复杂度吗？要的要的，我们这边二分 \(\log V\) 次，然后每一次复杂度是 \(n^{2}\log V\)
  很有意思！

[ARC176E]

这hint有什么用吗？
好的，注意到值域不大，考虑如何刻画取 max 这个限制。我们序列每个都会被分配给 \(X,Y\) 其中一个，考虑最小割，虽然不知道里面细节是啥，但是可以想象是 \(S\rightarrow X\rightarrow A \rightarrow Y\rightarrow T\) 这样的结构。值域不大，所以我们对于值域建点。
我们发现取 max 相当于，如果 \(X_{i}<A_{i}\) 那么 \(Y_{i}\) 就必须 \(\ge A_{i}\) 有这个限制就足够了。
先对每一位独立起来看，我们对每个 \(X_{i}\) 和 \(Y_{i}\) 建 501个点，代表当前的取值。注意到我们要求的是 \(\sum\limits_{i=1}^{n} X_{i}+Y_{i}\) 所以我们值域点连向下一个的容量就是 \(X_{i}\) 一旦有一个 \(A_{i}\) 向 \(X_{i}\) 连边了，那么连的那个点出去的那条边就是 \(A_{i}\)。还是从最小割的角度考虑，那么这个建图就很清晰了。对于每个 \(X_{i}\) 和 \(Y_{i}\) 我们都建 501 个点代表值，然后 \(X\) 的链是正的，\(Y\) 的链是倒的，\(X_{i,A_{i}}\rightarrow A_{i} \rightarrow Y_{i,A_{i}+1}\) 这样代表如果 \(S\) 和 \(X_{i,A_{i}}\) 下面的点联通，也就是 \(X_{i}\) 的取值 \(<A_{i}\) 那么 \(Y_{i}\) 就 \(\ge A_{i}\)。那是否要从 \(Y_{i}\) 向 \(X_{i}\) 连边呢？还是从最小割的角度考虑。那么我们考虑对整个操作绑定，那也就是对整个操作建虚点，然后只能让操作点之间连的边被割掉，而其它边不会被割掉。
有点混乱，我们把这个看作很多很多柱子，然后你可以从中间切开，中间切开那么就是最小割。

好图！我们 \(X_{i}\) 初始连到 \(T\)，那么就不可能割 \(X_{i,X_{i}}\) 下面的边，如果\(X_{i}\) 割比 \(A_{i}\) 下面的边，那么 \(Y_{i}\) 就要割下面的边，这是为了保证最小割的性质，可以理解。\(X_{i}\) 割上面的边就貌似没啥关系了。首先这样的割一定是合法的，会不会出现 \(Y_{i}<A_{i}\) 并且 \(X_{i}<A_{i}\) 的情况，因为我们是割，那么这个就是合法的。然后我们的最小割会自动找到这个最小值。操作绑定按上面的来搞差不多了。
具体而言，会不会出现 \(X_{i}<A_{i}\) 并且 \(Y_{i}\ge A_{i}\) 的