数论学习笔记

合集 - 学习笔记(14)

1.关于导数问题的一些粗浅思考2024-02-27

2.数论学习笔记2024-02-27

3.模拟退火学习笔记2024-02-274.单调队列+决策单调性dp学习笔记2024-02-275.前中后缀表达式学习笔记2024-02-276.关于dfs序求lca的一点思考2024-02-277.P1240+P1350+ AT_abc282_g得出的一些dp技巧2024-02-278.关于线段树合并维护树上信息的一点思考2024-02-279.关于一些合并操作加维护信息的一类题的思考2024-02-2710.状压dp学习笔记2024-02-2911.由POJ1821得出的一些dp优化技巧2024-02-2912.tarjan学习笔记2024-04-2113.manacher学习笔记2024-05-2014.hall 定理学习笔记2024-07-29

收起

写在前面

$a\mod b=(a-\left \lfloor \frac{a}{b} \right \rfloor *b)$

代数推导天地灭，组合意义保平安

1.辗转相减

利用辗转相减法求最大公约数, 即 $gcd(a, b)$。假设 $a > b$, 则 gcd(a, b) =gcd(a − b, b), 不断的利用大的数减去小的数，就能得到最大公约数。

1.证:若$n,m(n>m)$互质，则 $(n-m) , m$互质

若不互质,则设 $n - m = k * a , m = k * b$

$\therefore n-k*b=k*a$

$\therefore n=k*(a+b)$，与n,m互质矛盾,得证

我们发现当 a 一直大于 b 的时候，就会一直减去 b，其实就是变成 a%b，所以就变成了辗转相除

2.扩展欧几里得(exgcd)

解的存在性:

裴蜀定理

对于任意n个整数，存在以种线性组合使得其等于所有数的最大公约数。

若$a,b$是整数,且$gcd(a,b)=k$，那么对于任意的整数$x,y,ax+by$都一定是k的倍数。

证：一定存在整数$x,y$，使$ax+by=gcd(a,b)$成立。

不太好证，采用数形结合的方法

皮克定理 : 给定顶点坐标均是整点（或正方形格点）的简单多边形，面积$S$和内部格点数目$n$、多边形边界上的格点数目$k$：$S=n+\frac{k}{2} -1$

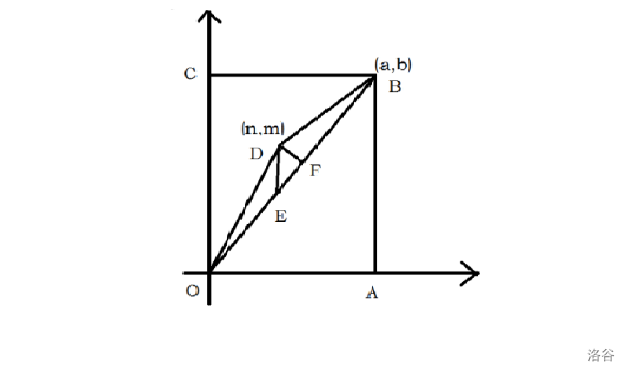
$\because \gcd(a, b)=1$

$\therefore AO$上无整点

在矩形$ABCO$中找离$AO$最近的格点$P(n,m)$

$\Delta A P O$ 边界上和内部无整点(如果有的话那个点肯定跟优,与假设矛盾)

$\therefore S\Delta A P O=0+\frac{3}{2}-1=\frac{1}{2}$

$\because AO=\sqrt{a^2+b2} $

$\therefore PH=\frac{\left |bn-am \right |}{\sqrt{a^2+b^2} }$ (点到直线距离公式)

$\therefore S\Delta A P O=\frac{1}{2}\sqrt{a^2+b^2} *\frac{\left |bn-am \right |}{\sqrt{a^2+b^2} }=\frac{1}{2}\left |bn-am \right |$

$\therefore \left |bn-am \right |=1$

所以当$\left{ $$\begin{matrix} x=m \ y=-n \end{matrix}$$ \right. $或$\left{ $$\begin{matrix} x=-m \ y=n \end{matrix}$$ \right. $时等式成立

所以当 c 是 gcd(a, b) 的倍数的时候,方程有解，将x,y同时扩大多少倍即可

若$b*x_{1}+a \bmod b *y_{1}=\gcd(a, b)$

$\therefore b*x_{1}+(a-\left \lfloor \frac{a}{b} \right \rfloor *b) *y_{1}=\gcd(a, b)$

$\therefore a*y_{1}-b*(x_{1}-\left \lfloor \frac{a}{b} \right \rfloor *y_{1}) =\gcd(a, b)$

$\therefore x=y1,y=x_{1}-\left \lfloor \frac{a}{b} \right \rfloor *y_{1}$

(代码有些不好理解)
exgcd大致分为两步:
先求出gcd 然后利用这个gcd解出一个解(不是真真的解)，然后不断扩大

long long exgcd(long long a,long long b,long long &x,long long &y){
	int d=a;
	if(b!=0){
		d=exgcd(b,a%b,x,y);
		x-=a/b*y;
		swap(x,y);
	}
	else{
		x=1,y=0;
	}
	return d;
}

3.乘法逆元

设$\frac{a}{b} \bmod p = x$

$\therefore \frac{a}{b} \equiv x \bmod p$

$\therefore a \equiv bx \pmod{p}$

设 $a \bmod p=k_{1}.....n$

$bx \bmod p=k_{2}.....n$

$\therefore k_{1}*p+n=a,k_{2}*p+n=bx$

$\therefore k_{2}*p+a-k_{1}*p=bx$

$\therefore a+p*(k_{2}-k_{1})=bx$

$\therefore p*(k_{1}-k_{2})+bx=a$

既然a,b,p都知道，我们就可以用exgcd啦

有理数取余

$\frac{a}{b} \equiv x \pmod{p}$

$a \equiv bx \pmod{p}$

先求$1 \equiv bx_{1} \pmod{p}$

再将$a \equiv b*a*x_{1} \pmod{p}$

$a*x_{1}即为所求答案$

4.高斯消元

非常好理解，之前我被 @【数据删除】称为高斯消元高手，为了不负期望，我决定复习一次。

#include<iostream>
using namespace std;
int n,st;
double a[105][105];//第i个方程的第j个未知数的系数
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n+1;j++){
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		int st=i;
		for(int j=i+1;j<=n;j++){
			if(a[j][i]>a[st][i]){//选取一个最大值减小误差
				st=j;
			}
		}
		for(int j=1;j<=n+1;j++){
			swap(a[i][j],a[st][j]);//i和st对换
		}
		if(a[i][i]==0){
			puts("No Solution");
			return 0;
		}
		for(int j=1;j<=n+1;j++){
			if(i!=j){
           //当前消到第i个未知数，那么当做到第j个方程时，其第i个未
           //知数的系数就是a[j][i]，那么这个方程就应该整体减去
           //a[j][i]/a[i][i]倍的方程i
				for(int k=i+1;k<=n+1;k++){//前面已经都是0了
					a[j][k]-=a[i][k]*a[j][i]/a[i][i];
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
		printf("%.2lf\n",a[i][n+1]/a[i][i]);
	}
	
	return 0;
}

CRT:

好文

不妨验证解为什么正确。以第一个方程为例因为乘了最小公倍数，因为两两互素那么其他乘上逆元不会对
模$mod1$ 产生影响假设其他数乘起来也就是$M1$模$mod1$那么我们只需将这个模数扩大即可。所以要求下逆元再乘$a1$就可以了

EXCRT

这个不可以用在crt上吗qwq
考虑合并
$x=k1*mod1+a1$

$x=k2*mod2+a2$

$k1*mod1+a1=k2*mod2+a2$

$a1-a2=k2*mod2-k1*mod1$

使用exgcd求出特解$k1$

将$k1$带回去就是x那么x的通解就是$x+k*lcm(mod1,dmo2)$

逻辑运算

eeeeeeee,学学玩的

1. 对于一个仅由$\land$或$\lor$(加不加$!$)都一样是满足交换律的,枚举易证.

2. $!(p \land q)=!p \lor !q$

3. $!(p \lor q)=!p \land !q$

4. 韦恩图很厉害,能解决三个命题以下的问题

写于8月28的莫反，今天励志要学懂。莫反听一遍不懂一遍

一、数论分块

1.最大的使$\lfloor{\frac{n}{x}} \rfloor=\lfloor{\frac{n}{i}} \rfloor$的x是$\lfloor{\frac{n}{\lfloor{\frac{n}{i}} \rfloor}} \rfloor$

证:
设$\lfloor{\frac{n}{i}} \rfloor=k$

$\because k \le \frac{n}{i}$

$\therefore \lfloor{\frac{n}{k}}\rfloor \ge \lfloor{\frac{n}{\frac{n}{i}}}\rfloor$

$\therefore \lfloor{\frac{n}{k}}\rfloor \ge i$

$\therefore i \le \lfloor{\frac{n}{k}}\rfloor$

因为k是定值，那么i的最大值就是$\lfloor{\frac{n}{\lfloor{\frac{n}{i}} \rfloor}} \rfloor$

二、积性函数

证:$\phi$为积性函数

$\phi (n)=n*\prod_{p1|n}(1-\frac{1}{p1})$

$\phi (m)=m*\prod_{p2|m}(1-\frac{1}{p2})$

$\gcd(n,m)=1$

因为互质，所以任意p1都不等于p2，得证

证:$\sum_{d|n} \phi(d)=n$

OI-wiki上的证法比zb妙一点。

首先设$f(x)为gcd(i,n)=x的i的个数$

$\sum_{i=1}^{n} f(i)=n$（显然）

$\sum_{d|n} f(d)=n$

考虑f和$\phi$的关系

显然$f(x)=\phi(\frac{n}{x})$

然后因为对称性就完了

常见积性函数

单位函数$e(n)=[n=1]$

幂函数$id_{k}(n)=n^{k}$其中$id_{1}(n)$常被记作$id(n)$

常函数$k(n)=k$

除数函数$\sigma_{k}(n)=\sum_{d|n} d^{k}$当$k=0$时为因数个数函数$d(n)$当$k=1$时为因数和函数为$\sigma(n)$

欧拉函数$\phi(n)=\sum[gcd(i,n)=1]$

莫比乌斯函数
$\mu(n)= \begin{rcases} 1\ \ \ \ \ \ \ \ \ \ \ \ n=1 \\ 0\ \ \ \ \ \ \ \ \ \ \ \ n有平方因子 \\ (-1)^{k} ,k为n的本质不同质因子个数 \end{rcases}$

三、莫比乌斯函数

证积性

感性一下，如果和$\mu(1)$乘显然，然后和不为1的乘也显然

证$\sum_{d|n} \mu(d)=[n=1]$

设$n=\prod p_{i}^{c_{i}},m=\prod p_{i}$

原式$=\sum_{d|m} \mu(d)=[m=1]$

设因数个数为$k$

$\sum_{d|m} \mu(d)=\sum_{i=0}^{k} {k\choose i} (-1)^{i}$

$=\sum_{i=0}^{k} {k\choose i} (-1)^{i}*1^{k-i}$

二项式定理

$=((-1)+1)^{k}$

线性筛求miu

void get(){
    miu[1]=1;
    for1(i,2,n){
        if(!vis[i]){
            miu[i]=-1;
            cnt++;
            num[cnt]=i;
        }
        for(int j=1;i*num[j]<=n&&j<=cnt;j++){
            vis[i*num[j]]=1;
            if(i%num[j]==0){
                miu[i*num[j]]=0;
                break;
            }
            miu[i*num[j]]=-miu[i];
        }
    }
}

四、狄利克雷卷积

* 表示卷积 ·表示乘。f,g为数论函数（定义域为整数的函数，通常值域也为整数）

$(f * g)(n)=\sum_{d|n} f(d)g(\frac{n}{d})$

证:若f,g为积性函数，那么f * g也是积性函数

$(f*g)(n)=\sum_{d|n} f(d)g(\frac{n}{d})$

$(f*g)(m)=\sum_{d|m} f(d)g(\frac{m}{d})$

$(f*g)(nm)=\sum_{d|nm} f(d)g(\frac{nm}{d})$

$(f*g)(n)*(f*g)(m)=\sum_{d|n} f(d)g(\frac{n}{d})·\sum_{d|m} f(d)g(\frac{m}{d})$

$(f*g)(n)*(f*g)(m)=\sum_{d1|n,d2|m} f(d1)g(\frac{n}{d1})f(d2)g(\frac{m}{d2})$

$(f*g)(nm)=\sum_{d1|n,d2|m} f(d1d2)g(\frac{nm}{d1d2})$

因为$\gcd(n,m)=1$

$(f*g)(nm)=\sum_{d|nm} f(d)g(\frac{nm}{d})$

$id_{k}*1=\sigma_{k}$

$(id_{k}*1)(n)=\sum_{d|n}id_{k}(d)$

$(id_{k}*1)(n)=\sum_{d|n}d^{k}$

$\phi*1=id$

$(\phi*1)(n)=\sum_{d|n} \phi(d)$

$(\phi*1)(n)=n$

五、狄利克雷卷积的性质

交换律

对称性易得

结合律

$(f*g)*h(n)=f*(g*h)(n)$

左式$=\sum_{d|n} (f*g)(d)h(\frac{n}{d})$

$=\sum_{d|n} h(\frac{n}{d})\sum_{d1|d} f(d1)g(\frac{d}{d1})$

右式$=\sum_{d|n} (g*h)(d)f(\frac{n}{d})$

$=\sum_{d|n} f(\frac{n}{d})\sum_{d1|d} g(d1)h(\frac{d}{d1})$

因为都穷尽了将$n=a·b·c$的方案，所以相等

分配律

$f*(g+h)(n)=f*g(n)+f*h(n)$

原式$=\sum_{d|n} f(d)*(g(\frac{n}{d})+h(\frac{n}{d}))$

$=\sum_{d|n} f(d)*g(\frac{n}{d})+\sum_{d|n} f(d)*h(\frac{n}{d})$

即$f*g(n)+f*h(n)$

单位元e

任何函数卷e都是自己

$\sum_{d|n} f(d)e(\frac{n}{d})$
当d=n时e为1，其他都为0，即为$f(n)$

证 $e=\mu *1$

原式$=\sum_{d|n} \mu(d)$

即为$e$

证 $\mu * id=\phi$

$\because \phi*1=id$

$\therefore \phi=id*\mu$

狄利克雷逆元

若$f*g=e$那么g就是f的逆元，g记作$f^{-1}$

证 $f^{-1}$为

$\begin{rcases} \frac{1}{f(1)} \ \ \ \ \ \ \ \ \ \ \ \ n=1 \\ -\frac{1}{f(1)}\sum_{d|n,d>1} f(d)g(\frac{n}{d})\ \ \ \ otherwise \end{rcases}$

当n=1时

$\sum_{d|1} f(d)g(\frac{n}{d})$

$=f(1)g(1)=1$

$g(1)=\frac{1}{f(1)}$

else

$\sum_{d|n} f(d)g(\frac{n}{d})=0$

$=f(1)g(n) \sum{d|n,d>1} f(d)g(\frac{n}{d})$

$=f(1)*(-\frac{1}{f(1)}\sum_{d|n,d>1} f(d)g(\frac{n}{d}))+\sum{d|n,d>1} f(d)g(\frac{n}{d})=0$

得证

证积性函数的逆元也是积性函数

不会，但很好记

五、莫比乌斯反演的证明

$f(n)=(g*1)(n)=\sum_{d|n} g(d)$

$g(n)=(f*\mu)=\sum_{d|n} f(d)\mu(\frac{n}{d})$

$f=g*1$那么$g=f*\mu$

$f=g*1$

$f*\mu=g*1*\mu$

$f*\mu=g*e$

$f*\mu=g$

交换求和顺序

是个很好用的东西

$\sum_{i=1}^{n}\sum_{j=1}^{m} a_{i,j}=\sum_{j=1}^{m}\sum_{i=1}^{n} a_{i,j}$

$\sum_{i=1}^{n}\sum_{j=i}^{m} a_{i,j}=\sum_{j=1}^{m}\sum{i=1}^{j} a_{i,j}$

$\sum_{i=1}^{n}\sum_{j=1}^{i} a_{i,j}=\sum_{j=1}^{m}\sum{i=j}^{n} a_{i,j}$

上面几个画图很好理解，还可以通过考虑贡献来解决

若是更一般的求和式，如何处理呢？
交换原则：入内求交，出外求并
意思是：外层变量移动到内层，需要将内外限制条件取交以限制它；
而内层变量移动到外层，需求内外限制条件的并。

外层 $i \in A$, 内层 $j \in B(i)$,

-> 外层 $j \in \bigcup B(i)$, 内层 $i \in {i \in A | j \in B(i)}$

将上面的用一下试试

$\sum_{i=1}^{n}\sum_{j=i}^{n} a_{i,j}$

j的范围$\bigcup^{n}_{i=1} [i,n]=[1,n]$
i的范围$[1,n]\bigcup[j,n]=[1,j]$
i的范围来自于i自己的限定和如果固定j对i的限定

$\sum_{i=1}^{n}\sum_{j=1}^{i} a_{i,j}$
j的范围$\bigcup^{n}_{i=1} [1,i]=[1,n]$
i的范围$[1,n]\bigcap[j,n]=[j,n]$

例1:不会

$\sum_{i=1}^{n} \phi(i)\lfloor{\frac{n}{i}}\rfloor$
$\sum_{i=1}^{n} \phi(i) \sum_{i|j}^{n} 1$
$\sum_{i=1}^{n} \sum_{i|j}^{n} \phi(i)$
$\sum_{j=1}^{n} \sum_{i|j} \phi(i)$
$\sum_{j=1}^{n} j$
$\frac{n*(n+1)}{2}$

例2:莫比乌斯反演的另一种证法

已知$f(n)=\sum_{d|n} g(d)$

求证$g(n)=\sum_{d|n} f(\frac{n}{d})\mu(d)$

原式$=\sum_{d|n} \sum_{d1|\frac{n}{d}} g(d1)\mu(d)$

$=\sum_{d|n} \sum_{d1|\frac{n}{d}} g(d1)\mu(d)$

---

交换原则：入内求交，出外求并

d1范围，显然d1范围是d1|n,因为对称性，将$d1|\frac{n}{d}$变为$d1|n$易证

d范围，考虑d1固定时对d有什么限制。$\frac{n}{d}$为$d1$倍数，那么d就为\frac{n}{d1}因数，证明:

$\frac{n}{d}=k·d1$

$\frac{n}{d1}=k·d$

---

$=\sum_{d1|n} \sum_{d|\frac{n}{d}} g(d1)\mu(d)$

$=\sum_{d1|n} g(d1)\sum_{d|\frac{n}{d1}} \mu(d)$

$=\sum_{d1|n} g(d1) [\frac{n}{d1}=1]$

$=g(n)$

请注意：求并操作做了n次，这是因为内层变量在枚举过程中受到外层n次限制。而求交操作只做一次，因为内层无论怎么变，对外层没有影响，提到外面，范围作形式保留

常见的5个数论函数线性筛求法

交换求和技巧

比较全的笔记