【洛谷 8601】[蓝桥杯 2013 省 A] 剪格子

# [蓝桥杯 2013 省 A] 剪格子

## 题目描述

如图 $1$ 所示，$3\times 3$ 的格子中填写了一些整数。


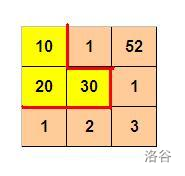
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 $60$。

本题的要求就是请你编程判定：对给定的 $m\times n$ 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 $0$。

## 输入格式

程序先读入两个整数 $m$，$n$ 用空格分割 $(m,n<10)$
表示表格的宽度和高度。

接下来是 $n$ 行，每行 $m$ 个正整数，用空格分开。每个整数不大于 $10000$。

## 输出格式

程序输出：在所有解中，包含左上角的分割区可能包含的最小的格子数目。

## 样例 #1

### 样例输入 #1

```
3 3
10 1 52
20 30 1
1 2 3
```

### 样例输出 #1

```
3
```

## 样例 #2

### 样例输入 #2

```
4 3
1 1 1 1
1 30 80 2
1 1 1 100
```

### 样例输出 #2

```
10
```

## 提示

第二个用例中：


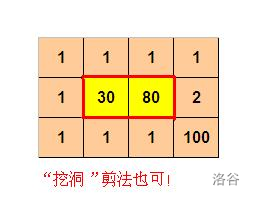
时限 5 秒, 64M。蓝桥杯 2013 年第四届省赛

 

题解：注意dfs是错解：因为可能

3

1 1 1

8 1 1

1 1 1

就没有办法dfs解决，因为dfs本质上是解决“一笔画问题”，卡错

样例较小时可以解决，较大则不可以

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<bits/stdc++.h>
using namespace std;
int ans=1e9,X,Y,n,m,a[12][12],sum,f[12][12];
//int dx[6]={1,0,0,-1};
//int dy[6]={0,1,-1,0};
int b[4][2]={{1,0},{0,1},{0,-1},{-1,0}};
void dfs(int x,int y,int sm,int now){
    if(sm==sum/2){
        if(now<ans && f[1][1]==1) ans=now;
        return ;
    }
    if(sm>sum/2) return ;
    for(int i=0;i<4;i++){
        //X=x+dx[i]; Y=y+dy[i];
        X=x+b[i][0]; Y=y+b[i][1];
        if(X<1 || X>n || Y<1 || Y>m) continue;
        if(f[X][Y]==1) continue;
        
        f[X][Y]=1; 
        dfs(X,Y,sm+a[X][Y],now+1);
        if(ans) return;
        f[X][Y]=0;
        
    }
    return ;
}

int main(){
    freopen("8601.in","r",stdin);
    freopen("8601.out","w",stdout);
    scanf("%d %d",&m,&n);
    //n为行数（高度），m为列数 
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
            sum+=a[i][j];
        }
    if(sum%2!=0){
        printf("0\n");
        return 0;
    }    
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            memset(f,0,sizeof(f));
            f[i][j]=1; 
            dfs(i,j,a[i][j],1);
        }
    printf("%d\n",ans);
    return 0;
}