【洛谷 5020】货币系统

题目描述

在网友的国度中共有 nn 种不同面额的货币，第 ii 种货币的面额为 a[i]a[i]，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 nn、面额数组为 a[1..n]a[1..n] 的货币系统记作 (n,a)(n,a)。

在一个完善的货币系统中，每一个非负整数的金额 xx 都应该可以被表示出，即对每一个非负整数 xx，都存在 nn 个非负整数 t[i]t[i] 满足 a[i] \times t[i]a[i]×t[i] 的和为 xx。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 xx 不能被该货币系统表示出。例如在货币系统 n=3n=3, a=[2,5,9]a=[2,5,9] 中，金额 1,31,3 就无法被表示出来。

两个货币系统 (n,a)(n,a) 和 (m,b)(m,b) 是等价的，当且仅当对于任意非负整数 xx，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)(m,b)，满足 (m,b)(m,b) 与原来的货币系统 (n,a)(n,a) 等价，且 mm 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 mm。

输入格式

输入文件的第一行包含一个整数 TT，表示数据的组数。

接下来按照如下格式分别给出 TT 组数据。 每组数据的第一行包含一个正整数 nn。接下来一行包含 nn 个由空格隔开的正整数 a[i]a[i]。

输出格式

输出文件共有 TT 行，对于每组数据，输出一行一个正整数，表示所有与 (n,a)(n,a) 等价的货币系统 (m,b)(m,b)中，最小的 mm。

输入输出样例

输入 #1复制

2 
4 
3 19 10 6 
5 
11 29 13 19 17 

输出 #1复制

2   
5  

说明/提示

在第一组数据中，货币系统 (2, [3,10])(2,[3,10]) 和给出的货币系统 (n, a)(n,a) 等价，并可以验证不存在 m < 2m<2 的等价的货币系统，因此答案为 22。 在第二组数据中，可以验证不存在 m < nm<n 的等价的货币系统，因此答案为 55。

【数据范围与约定】

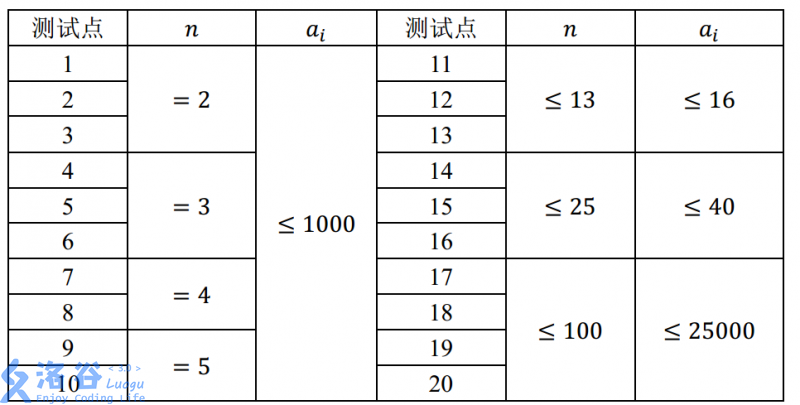
对于 100\%100% 的数据，满足 1 ≤ T ≤ 20, n,a[i] ≥ 11≤T≤20,n,a[i]≥1。

 

 

题解：原来去年题目这么水！！！蛮简单的呀QAQ。就是类似于筛法。

          把一些不必要的金钱都舍掉，比如有3，则6,9,12都是多余的，先排序

          从小到大枚举。则大的肯定会被小的筛掉，最后看有多少个“必要金钱”即可。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<queue>
using namespace std;
const int N=103;
int Yao_Chen,n,ans,mx;
int a[N],f[25005];
int main(){
    freopen("5020.in","r",stdin);
    freopen("5020.out","w",stdout);
    scanf("%d",&Yao_Chen);
    while(Yao_Chen--){
        scanf("%d",&n); ans=0; mx=0;
        memset(f,0,sizeof(f));
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            mx=max(mx,a[i]); f[a[i]]=2;
        }   
        sort(a+1,a+n+1);
        for(int i=1;i<=mx;i++){
            if(f[i]>0){
                for(int j=1;j<=n;j++){
                    if(i+a[j]<=mx) f[i+a[j]]=1;
                    else break;
                }
            }
        } 
        for(int i=1;i<=mx;i++)
            if(f[i]==2) ans++;
        printf("%d\n",ans);
    }
    return 0;
}