【洛谷 3953】宝藏

题目描述

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 nn 个深埋在地下的宝藏屋， 也给出了这 nn 个宝藏屋之间可供开发的mm 条道路和它们的长度。

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远， 也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路 则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。

新开发一条道路的代价是：

\mathrm{L} \times \mathrm{K}L×K

L代表这条道路的长度，K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋） 。

请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代 价最小，并输出这个最小值。

输入格式

第一行两个用空格分离的正整数 n,mn,m，代表宝藏屋的个数和道路数。

接下来 mm 行，每行三个用空格分离的正整数，分别是由一条道路连接的两个宝藏 屋的编号（编号为 1-n1−n），和这条道路的长度 vv。

输出格式

一个正整数，表示最小的总代价。

输入输出样例

输入 #1复制

4 5 
1 2 1 
1 3 3 
1 4 1 
2 3 4 
3 4 1 
 

输出 #1复制

4

输入 #2复制

4 5 
1 2 1 
1 3 3 
1 4 1 
2 3 4 
3 4 2  

输出 #2复制

5

说明/提示

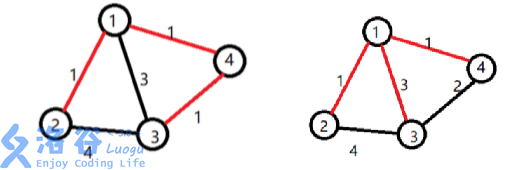
【样例解释1】

小明选定让赞助商打通了11 号宝藏屋。小明开发了道路 1 \to 21→2，挖掘了 22 号宝 藏。开发了道路 1 \to 41→4，挖掘了 44 号宝藏。还开发了道路 4 \to 34→3，挖掘了33号宝 藏。工程总代价为：1 \times 1 + 1 \times 1 + 1 \times 2 = 41×1+1×1+1×2=4

【样例解释2】

小明选定让赞助商打通了11 号宝藏屋。小明开发了道路 1 \to 21→2，挖掘了 22 号宝 藏。开发了道路 1 \to 31→3，挖掘了 33 号宝藏。还开发了道路 1 \to 41→4，挖掘了44号宝 藏。工程总代价为：1 \times 1 + 3 \times 1 + 1 \times 1 = 51×1+3×1+1×1=5

【数据规模与约定】

对于20\%20%的数据： 保证输入是一棵树，1 \le n \le 81≤n≤8，v \le 5000v≤5000 且所有的 vv都相等。

对于 40\%40%的数据： 1 \le n \le 81≤n≤8，0 \le m \le 10000≤m≤1000，v \le 5000v≤5000 且所有的vv都相等。

对于70\%70%的数据： 1 \le n \le 81≤n≤8，0 \le m \le 10000≤m≤1000，v \le 5000v≤5000

对于100\%100%的数据： 1 \le n \le 121≤n≤12，0 \le m \le 10000≤m≤1000，v \le 500000v≤500000

题解：我先写一个暴力 DFS拿了70分哦。

#include<iostream>
#include<algorithm>
#include<queue>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<cstdio>
using namespace std;
const int oo=0x3f3f3f3f;
int a[1001],f[1001];
int map[55][55];
int ans=oo,tmp,n,m,u,v,co;
void dfs(int e,int num){
    if(num==n){
        ans=min(tmp,ans);
        return;
    }//n个宝藏点都可以遍历到 
    if(tmp>=ans) return;//小小的剪枝，大大的优化 
    for(int i=1;i<=n;i++){//遍历到这个点 
        if(f[i]) continue;//被遍历到了,无需执行下去 
        for(int j=1;j<=n;j++){//i点是由j点推来的 
            if(map[j][i]==oo || !f[j] || i == j) continue;
            tmp+=f[j]*map[j][i]; f[i]=f[j]+1;
            dfs(i,num+1);
            tmp-=f[j]*map[j][i]; f[i]=0;//记忆化搜索里要清零！ 
        }
    }
}

int main() {
    freopen("treasure.in","r",stdin);
    freopen("treasure.out","w",stdout);
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            map[i][j]=oo;
    for(int i=1;i<=m;i++){
        scanf("%d %d %d",&u,&v,&co);
        map[u][v]=map[v][u]=min(map[u][v],co);
    }
    scanf("%d %d",&u,&v);
    for(int i=1;i<=n;i++){//这个点是"入口" 
        f[i]=1; dfs(i,1); f[i]=0;
    }
    printf("%d\n", ans);
    return 0;
}