HDU 4162 Shape Number

（先吐个槽：原文前面都是废话Orz）

题目的大概意思是给你一串数字编码，先两两相减（ b[1] = a[2] – a[1]，如果a[2] < a[1]，那么b[1] = (a[2] + 8) – a[1]  ）。得到一个处理过后的编码，然后把此编码视为循环编码，输出出字典序最小的编码。例如15011的编码有15011， 50111， 01115， 11150， 11501。其中，字典序最小的编码为：01115

第一步So easy，一个for循环就搞出来了。

第二步找字典序最小的排列，我一开始想到的是最朴素的算法，即枚举所有序列并对所有序列进行比较。这个我看到数据大小就跪了（Orz 身体前屈），原始编码最长为3 * 10 ^ 5 位，枚举直接TLE。之后还是用最小表示法写的。最小表示法相较于枚举，优化了每次移动的距离，可以节省大量时间（原理类似KMP）。

最小表示法利用 2 个指针 i, j 一开始分别指向第一个字符和第二个字符，然后引入一个变量 k ，初始值为0，用于存储相同位数。

接着比较 b[i + k] 和 b[j + k] 两者的大小：

较大的向后移动 k + 1 位。如果两者相等 k 自加 1

特别的，当i == j 的时候，j 自加 1。

当 i ，j，k 均小于总长度 len 的时候循环执行比较、移动。结束循环之后，取 i , j 中较小的一个为起始点，输出的编码为字符串最小的编码。

P.S：注意，我在处理循环编码的时候是用 % 取模，还可以通过扩展一倍的空间将编码存储2遍的方法来处理（例如: 123 存储为 123123）。

当使用后者时 i, k < len, j < 2 * len, 其中 len 为编码原长。

---

下面举个简单的例子来模拟最小表示法

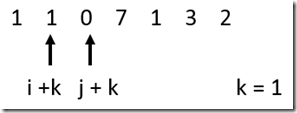
我已经把某段编码经过第一步处理得到了如下编码：

    

然后开始进行最小字典序的查找：

因为 b[i + k] = b[j + k]， 所以 k 自加 1。此时 i = 0，j = 1，k = 1

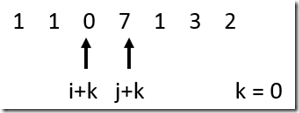
接着进行下一轮：

因为，b[i + k] > b[j + k]，所以 i 移动 k + 1位。此时 i = 2, j = 1, k = 0

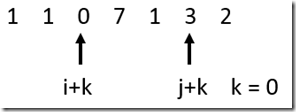
继续下一轮：

 

这次是b[i + k] < b[j + k]，所以 j 移动 k + 1位。此时 i = j = 2, k = 0。因为 i == j 所以 j 自加 1。变成3

继续下一轮：

同样b[i + k] < b[j + k]，所以 j 移动 k + 1位。此时 i = 2, j = 4, k = 0

同上，此时 i = 2, j = 5, k = 0

同上，此时 i = 2, j = 6, k = 0

同上，此时 i = 2, j = 7, k = 0。

因为 j == len，所以循环结束，以 i 和 j 中较小的为起点。此处为以 i 为起点。

所以，该编码的最小字典序排列为：

模拟完毕。附上AC代码：

#include <stdio.h>
#include <math.h>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <stdlib.h>
#include <string>
#include <list>
#include <vector>
#include <map>
#define Clean(x) memset(x, 0, sizeof(x))
#define LL long long
using namespace std;

int MinP(char *buf, int len)
{
    int i = 0, j = 1, k = 0, temp = 0;
    while (i < len && j < len && k < len)
    {
        temp = buf[(i + k) % len] - buf[(j + k) % len];
        if (temp == 0) k++;
        else
        {
            if (temp > 0)
                i += k + 1;
            else
                j += k + 1;
            if (i == j) j++;
            k = 0;
        }
    }
    return (i < j) ? i : j;
}
char buf[300009], buf2[300009];
int main()
{
    while (~scanf("%s", buf))
    {
        int len = strlen(buf);
        for (int i = 0; i < len; i++)
        {
            if (buf[i] > buf[(i + 1) % len])
                buf2[i] = buf[(i + 1) % len] - buf[i] + 8 + '0';
            else
                buf2[i] = buf[(i + 1) % len] - buf[i] + '0';
        }
        int s = MinP(buf2, len);
        for (int i = 0; i < len; i++, s = (s + 1) % len)
            putchar(buf2[s]);
        puts("");
    }
    return 0;
}