当折线的端点过于密集,以至于显示时堆积在一起时,有必要简化折线,以提高后续凸包或相交运算的处理效率与显示清晰度。关键问题是如何简化复杂折线,能够保持其特征,不至于失真。
第一步通过设置顶点之间的距离阈值来减少冗余顶点。
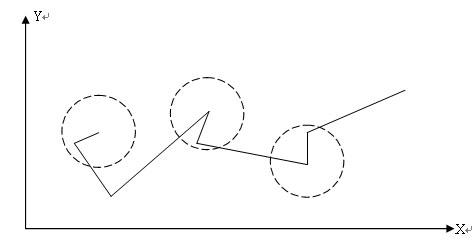
第二步,采用Douglas-Peucker (DP)算法简化折线,其在计算机图形学与地理信息系统领域被广泛应用。
其思想是顶点到某条边的距离过于接近的话,将被舍弃,保留距离大于阈值的顶点。初始化时,首先连接第一个和最后一个顶点构建第一条边,找到剩余顶点中距离这条线段最远的顶点,然后分别连接第一和最后一个顶点到此最远的顶点,构成两条线段,继续寻找剩余顶点中分别到这两条线段距离最远的顶点,依此类推,直到顶点到边的距离小于设置的阈值停止处理,那么找到的这些顶点构成了简化折线。

// 折线的简化程序,包含上述两步骤
// 输入: 阈值 tol,折线的顶点数组 V[],顶点的个数 n;
// 输出: 经过简化后的顶点数组 sV[];
// 返回: 简化后的顶点数组中的顶点数量 m;
int CDEMAlgorithm::poly_simplify( double tol, Point* V, int n, Point* sV )
{
int i, k, m, pv; //准备用做计数器
double tol2 = tol * tol; //阈值的平方
Point* vt = new Point[n]; // 输入的顶点数组
int* mk = new int[n]; //给标记数组初始化
for(i=0;i<n;i++)
{
mk[i] = 0; // 初始化
}
//第一步:通过顶点之间的距离判断,是否保留某些顶点
vt[0] = V[0];
for (i=k=1, pv=0; i<n; i++) { //对输入的每个顶点循环处理
if (d2(V[i], V[pv]) < tol2) //顶点之间的距离小于阈值,直接跳到下个顶点进行处理
continue;
vt[k++] = V[i]; //顶点之间的距离大于阈值,记录此顶点
pv = i; //记录此顶点的索引号
}
if (pv < n-1)
vt[k++] = V[n-1]; // 将最后一个顶点记录下来
//第二步:采用 Douglas-Peucker算法进行简化
mk[0] = mk[k-1] = 1; // 给第一个和最后一个顶点标记为1
simplifyDP( tol, vt, 0, k-1, mk );
// copy marked vertices to the output simplified polyline
for (i=m=0; i<k; i++) {
if (mk[i]) //如果标记为1的话
sV[m++] = vt[i]; //将顶点赋值给最后输出的结果数组
}
delete vt; //删除临时顶点数组
delete mk; //删除标记数组
return m; // m vertices in simplified polyline
}
// Douglas-Peucker (DP)算法
// 输入: 阈值tol,顶点数组v[],j,k分别指示顶点数组中的第一和尾部顶点,在第一次运行此程序片段时,表示连接最初和最后的顶点构成线段,在后面的递归调用中,表示连接到最远顶点的子线段;
// 输出: 简化后的顶点数组 mk[];
void CDEMAlgorithm::simplifyDP( double tol, Point* v, int j, int k, int* mk )
{
if (k <= j+1) // 两顶点挨在一起,没必要简化
return;
int maxi = j; // 准备记录距离线段的最远顶点的索引
double maxd2 = 0; // 准备记录最远距离的平方
double tol2 = tol * tol; // 设置的阈值的平方
Segment S = {v[j], v[k]}; // 构建 顶点v[j] 和 v[k]之间的线段
Vector u = S.P1 - S.P0; //矢量
double cu = Dot(u,u); // 线段长度的平方
// 采用前面讲解的顶点到线段的距离求法,计算每个顶点到线段S的距离
Vector w;
Point Pb;
double b, cw, dv2;
for (int i=j+1; i<k; i++)
{
w = v[i] - S.P0;
cw = Dot(w,u);
if ( cw <= 0 )
dv2 = d2(v[i], S.P0);
else if ( cu <= cw )
dv2 = d2(v[i], S.P1);
else {
b = cw / cu;
Pb = S.P0 + b * u;
dv2 = d2(v[i], Pb);
}
if (dv2 <= maxd2)
continue;
// v[i]是符合要求的最远顶点
maxi = i;
maxd2 = dv2;
}
if (maxd2 > tol2) // 如果最远顶点到线段S的距离大于阈值
{
mk[maxi] = 1; //记录maxi这个索引, 此顶点将被最后输出
//递归调用此程序
simplifyDP( tol, v, j, maxi, mk ); // 第一条子线段
simplifyDP( tol, v, maxi, k, mk ); // 第二条子线段
}
return;
}





