介绍求取平面上顶点集合凸包的Graham Scan和Andrew's Monotone Chain方法。基本原理是在顶点排序好后,初始化一栈,循环取出顶点集合中每个顶点元素,将其与栈顶两元素进行判别,看是否符合凸包条件,循环结束后,栈中剩余元素即为所求。具体过程如下。
求凸包Graham Scan方法。它的大致过程是:
找到最右下顶点P0后,以各顶点与P0X的夹角来排序所有的集合中顶点。实际工作中,可简化角度计算工作,而通过前面章节介绍的isLeft()函数,来判断顶点P2是否处于线段P0P1左边,从而判断夹角的大小。设这些经过排序的顶点为P0,P1,…Pn-1;
邻接关系判断图 
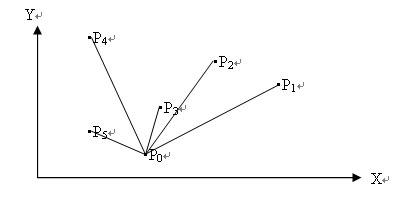
将顶点排好序
然后,建立一个栈,最开始时P0,P1进栈,对于剩下的顶点P2,P3,…Pn-1等依次取出,若栈顶的开头两个顶点与新取出的顶点不满足“左转”(即isLeft()函数返回数值大于0)条件,则将栈顶的第一个顶点出栈,继续测试,直到满足“左转”条件后将新取出的顶点进栈;所有剩下的顶点P2,P3,…Pn-1处理完之后栈中剩下的顶点构成凸包。
需说明的是,此方法很难推进到三维空间。
参考代码:
//主程序
Stack GrahamScan( )
{
Stack top;
int i;
Point p1, p2;
top = NULL;
top = Push ( &P[0], top );
top = Push ( &P[1], top ); //初始化栈
i = 2;
while ( i < n ) //对所有的排序后顶点循环
{
if( !top->next) printf("Error"n"); //栈中没有第二个元素,报出错信息
p1 = top->next->p;
p2 = top->p; //取出栈顶的两个元素
if ( isLeft( p1->v , p2->v, P[i].v ) )//判断是否左转
{
top = Push ( &P[i], top ); //压栈
i++; //顶点计数器增加
}
else
top = Pop( top ); //退栈
}
return top; //栈中剩下的元素即为构成凸包的顶点
}
//开始准备工作中寻找所有顶点中右下角顶点
int FindLowest( void )
{
int i;
int m = 0;
for ( i = 1; i < n; i++ ) //对所有顶点循环
if ( (P[i].v[Y] < P[m].v[Y]) ||
((P[i].v[Y] == P[m].v[Y]) && (P[i].v[X] > P[m].v[X])) )
m = i;
return m; //返回右下角最低点索引
}
求凸包Andrew's Monotone Chain方法。
首先,依X轴和Y轴数值顺序排列所有顶点。

以最左(当X轴数值相同的时候,以Y轴数值最下和最上取顶点)至最右边的顶点(当X轴数值相同的时候,以Y轴数值最下和最上取顶点)连线,构成Lup,Llow等线段,将顶点集合分成上下两部分,分别使用类似于上面介绍的Graham Scan方法寻求子凸包,最后合并形成一个凸包(注意连接处顶点的重复存储)。
参考代码:
// 输入经过排序的顶点数组 P[],n为数组中顶点个数
// 输出: 凸包的顶点集合 H[]
// 返回: H[]中的顶点个数
int CDEMAlgorithm::chainHull_2D( Point* P, int n, Point* H )
{
// 输出的数组H[]被用作一个栈
int bot=0, top=(-1); // 指示栈底和栈顶
int i;
int minmin = 0, minmax; // 得到X轴最小情况下Y轴分别最小和最大顶点的索引
double xmin = P[0].x;
for (i=1; i<n; i++)
if (P[i].x != xmin) break; //顶点已经排好序,搜索开始阶段的X轴最小值
minmax = i-1; //记录X轴最小情况下Y轴最大顶点的索引
if (minmax == n-1) { // 如果出现极端情况,即所有顶点X轴数值都最小
H[++top] = P[minmin];
if (P[minmax].y != P[minmin].y) // 如果两顶点的Y轴数值不等,则可构成线段
H[++top] = P[minmax];
H[++top] = P[minmin]; // 将这两个顶点增加到输出的数组中
return top+1; //返回输出的数组中的顶点个数
}
int maxmin, maxmax = n-1; // 得到X轴数值最大情况下 Y轴数值分别最小和最大的顶点索引
double xmax = P[n-1].x;
for (i=n-2; i>=0; i--) //从顶点的原始数组中反向循环,因为顶点已排好序
if (P[i].x != xmax) break;
maxmin = i+1; //记录X轴数值最大情况下Y轴数值最小的顶点索引
H[++top] = P[minmin]; // 开始计算下半部分凸包,首先将X轴和Y轴数值都最小的顶点压入栈
i = minmax; //从X轴数值最小情况下Y轴数值最大的顶点开始计数
while (++i <= maxmin)
{
// 以X轴和Y轴数值最小顶点连接X轴最大和Y轴数值最小顶点建立低线
if (isLeft( P[minmin], P[maxmin], P[i]) >= 0 && i < maxmin)
continue; // 由于此顶点位于这根低线之上,所以忽略,继续下次循环
while (top > 0) // top是从最开始的-1计数,所以大于0的话,表明栈中至少有2个元素
{
if (isLeft( H[top-1], H[top], P[i]) > 0)
break; //表明P[i]顶点是需要的凸包中新顶点,结束循环
else
top--; //将栈顶元素出栈,继续循环
}
H[++top] = P[i]; // 将顶点P[i]压入栈
}
// 下面,计算上半部分的凸包顶点集合
if (maxmax != maxmin) // 如果X轴数值最大情况下Y轴有不同顶点存在
H[++top] = P[maxmax]; // 将X轴数值与Y轴数值最大的顶点压入栈
bot = top; // 记住准备增加元素到栈前已经存在的元素个数
i = maxmin; //从X轴数值最大情况下Y轴数值最小的顶点开始计数
while (--i >= minmax)
{
// 以X轴和Y轴数值最大顶点连接X轴最小和Y轴数值最大顶点建立高线
if (isLeft( P[maxmax], P[minmax], P[i]) >= 0 && i > minmax)
continue; // 由于此顶点位于这根高线之下,所以忽略,继续下次循环
while (top > bot) // top还是比开始记住的bot大,表明栈中至少有2个元素
{
if (isLeft( H[top-1], H[top], P[i]) > 0)
break; //表明P[i]顶点是需要的凸包中新顶点,结束循环
else
top--; //将栈顶元素出栈,继续循环
}
H[++top] = P[i]; // 将顶点P[i]压入栈
}
if (minmax != minmin) //如果X轴数值最小情况下Y轴有不同顶点存在
H[++top] = P[minmin]; // 把这最后一个顶点压入栈
return top+1; //返回输出的凸包数组中的顶点个数
}





