3D空间下直线与平面的交点
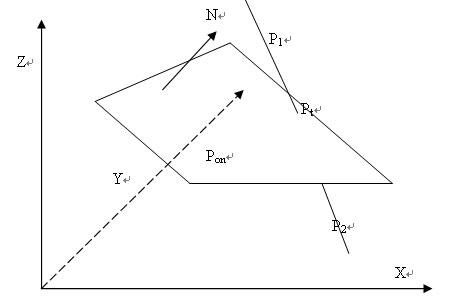
平面的已知条件为其法向量N(若法向量未知,可通过平面上任意两条直线矢量的叉乘求得),及其上任意一点Pon,直线的已知条件为其上两顶点P1,P2,现在要求此直线与平面的交点Pt,还是依照点乘与叉乘的定理这个思路来解决问题。
设 Pt = P1 + t(P2 ‐P1);现在求取参数t的大小;
因为Pt也是平面上的顶点,则矢量Pt Pon与法向量的点乘为0,可列方程:
(Pt ‐Pon) • N = 0;
(P1 ‐Pon)• N + t(P2 ‐P1)• N = 0;
则 t = ‐(P1 ‐Pon)• N /(P2 ‐P1)• N;
若分母(P2 ‐P1)• N = 0,则说明直线垂直于法向量,与平面是平行的,将无交点。若分子(P1 ‐Pon)• N = 0,则说明直线上的顶点与平面上顶点构成的向量垂直于法向量,即此顶点为交点或这个直线位于平面上。
参考代码
// 输入: 直线上的两个顶点p1, p2;平面的法向量和其上任意一顶点 pNormalofPlane
// 输出: 若存在的话,输出直线与平面的交点 *I0
// Return: 0 代表没有交点
// 1 代表存在唯一的交点 *I0
// 2 代表直线上顶点为交点或整个直线位于平面上
int CDEMAlgorithm::Intersect3D_LinePlane( XYZ p1,XYZ p2, XYZ pNormalofPlane, XYZ pOnPlane,XYZ* I )
{ Vector u = p2 - p1;
Vector w = p1 - pOnPlane;
double D = Dot(pNormalofPlane, u); //点乘
double N = -Dot(pNormalofPlane, w); //点乘
if (fabs(D) < EPS) { // 直线与平面平行
if (N == 0) // 顶点为交点或这个直线位于平面上
return 2;
else
return 0; // 交点不存在
}
double t = N / D;
*I = p1 + t*(p2 - p1); // compute segment intersect point
return 1;
}
点到平面的距离
点到平面的距离问题可转化为首先求垂心,再求两顶点之间的距离。
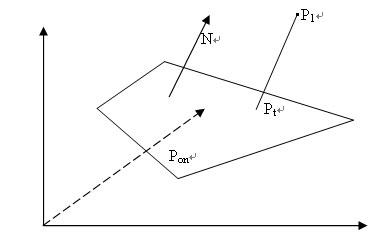
平面的已知条件为其法向量N,及其上任意一点Pon,已知一顶点P1,现在要求此顶点到平面的垂线交点Pt,
因为矢量PtP1垂直与平面,而垂直于平面的法向量为N,所以可将Pt设定为:
Pt = P1 + tN;现在求取参数t的大小;
因为Pt也是平面上的顶点,则矢量Pt Pon与法向量的点乘为0,可列方程:
(Pt ‐Pon) • N = 0;
(P1 ‐Pon)• N + tN• N = 0;
则 t = ‐(P1 ‐Pon)• N /N• N;
若分子(P1 ‐Pon)• N = 0,则说明顶点与平面上顶点构成的向量垂直于法向量,即此顶点位于平面上,Pt = P1。
参考代码与上面介绍的函数类似。
3D空间下直线到平面的距离
有前面介绍的内容后,求取3D空间下直线到平面的距离变得容易,在判断直线不完全落在平面上或与出现与平面相交的情况后,即此直线将与平面平行。取直线上任意一顶点,按照介绍的点到平面的距离方法,可求得直线到平面的距离。
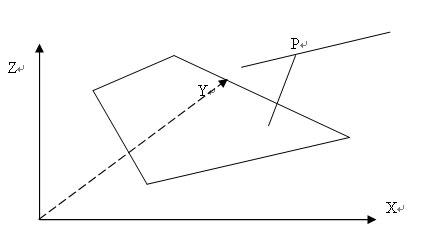
3D空间下两平面相交,一般形成交线。
交线既同时属于两个平面,则垂直于这两个平面的法向量,计算两个法向量的叉乘(前面已经证明,叉乘形成的矢量垂直于此两矢量),即为这条交线的方向。再找到这条交线上的一个顶点,可确定直线方程。

设两平面上的已知顶点为Ps,Pt,法向量为U,V,要寻找的交线上的顶点为Pw,由于平面上的顶点相减得到的矢量与法向量点乘为0,有方程组:
( Pw ‐ Ps)• U = 0
( Pw ‐ Pt)• V = 0
此方程组含有两个方程,但3个未知数(Pw的x,y,z轴数值),可令其中一个数值为0,从而求解方程组,得到另外两个未知数。
不妨设z = 0,可求得,
x = (V y Ps•U-Uy Pt•V) /(UxVy- VxUy);
y = (V x Ps•U-Ux Pt•V) /(UyVx- VyUx);
z = 0;
从几何上解释是,此顶点就是两平面和平面Z=0 交点。若两平面中有与平面Z=0情况出现,可以调整为与平面X = 0或Y = 0相交。
参考代码
// 输入: 两个平面,分别指定一个顶点和法向量
// 输出 : 若存在的话,将输出一条直线
// Return: 0 表示没有交线
// 1 表示两个平面共面
// 2 表示能得到一条唯一的交线
int CDEMAlgorithm::Intersect3D_2Planes( XYZ pNormalofPlane1, XYZ pOnPlane1, XYZ pNormalofPlane2, XYZ pOnPlane2, XYZ Linep1,XYZ Linep2 )
{
XYZ u;
u.x = pNormalofPlane2.y * pNormalofPlane1.z - pNormalofPlane2.z*pNormalofPlane1.y; u.y = pNormalofPlane2.x * pNormalofPlane1.z - pNormalofPlane2.z*pNormalofPlane1.x;
u.z = pNormalofPlane2.x * pNormalofPlane1.y - pNormalofPlane2.y*pNormalofPlane1.x; //以上三步,求得两个法向量的叉乘,即交线的方向矢量
double ax = (u.x >= 0 ? u.x : -u.x); //取正数
double ay = (u.y >= 0 ? u.y : -u.y);
double az = (u.z >= 0 ? u.z : -u.z);
//检测两平面是否能有交线
if ((ax+ay+az) < EPS) {
// 检测是共面还是平行
XYZ v = VectorSub(pOnPlane2,pOnPlane1);//将两平面上的已知顶点相减
if (Dot(pNormalofPlane1, v) == 0) //两平面上的顶点相减,形成的矢量与法向量垂直,说明共面
return 1; // 两平面是共面的
else
return 0; // 两平面是平行的,没有交线
}
int maxc;
if (ax > ay) {
if (ax > az)
maxc = 1;
else maxc = 3;
}
else {
if (ay > az)
maxc = 2;
else maxc = 3;
} //以上工作是:找到叉乘向量中的最大分量
// 找到两个平面形成的交线上的一点
// 让三个未知数中的一个为0,求另外两轴的未知数
XYZ iP; // 将要求得的顶点
double d1, d2;
d1 = -Dot(pNormalofPlane1, pOnPlane1); // 为前面分析工作中的 - Ps•U
d2 = -Dot(pNormalofPlane2, pOnPlane2); // 为前面分析工作中的 - Pt•V
switch (maxc) { // 根据最大的分量来确定哪根轴的数值为0
case 1: // 与x=0平面相交
iP.x = 0;
iP.y = (d2*pNormalofPlane1.z - d1*pNormalofPlane2.z) / u.x;
iP.z = (d1*pNormalofPlane2.y - d2*pNormalofPlane1.y) / u.x;
break;
case 2: // 与 y=0平面相交
iP.x = (d1*pNormalofPlane2.z - d2*pNormalofPlane1.z) / u.y;
iP.y = 0;
iP.z = (d2*pNormalofPlane1.x - d1*pNormalofPlane2.x) / u.y;
break;
case 3: // 与 z=0平面相交
iP.x = (d2*pNormalofPlane1.y - d1*pNormalofPlane2.y) / u.z;
iP.y = (d1*pNormalofPlane2.x - d2*pNormalofPlane1.x) / u.z;
iP.z = 0;
}
Linep1 = iP; //交线上的一个顶点
Linep2 = VectorAdd(iP , u); //交线上的另外一个顶点
return 2;
}





