图论简介

这里介绍图论（Graph Theory），图论是计算机科学中非常重要的一部分内容，甚至可以单独划分成为一个领域。很多人第一次接触到图论这个词，就觉得图论是研究和图画相关的内容。

   

     

不过当大家真的去学习图论时，可能大多数人都会失望一下子，因为图论实际上研究的是由顶点和边组成的一种数学模型，这种数学模型非常抽象，并且看起来也很枯燥。

   

 

虽然图论看起来很枯燥，但是如果大家真正的深入研究下去，就会发现图论是一个非常酷的学科。世界中很多的信息之间的联系，都可以使用图这种抽象的数学方式来进行表示，如下就是表示互联网之间关系的连接图。

   

   

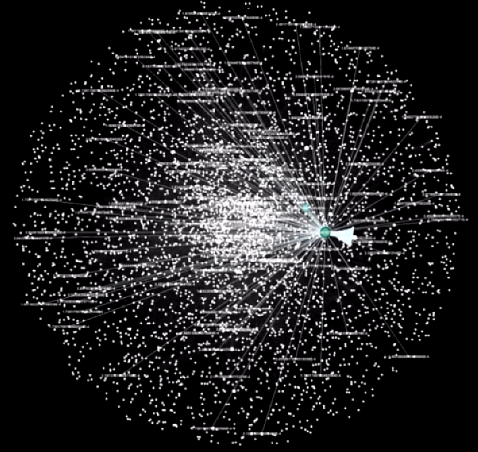
通过建造这样的模型，可以得出很多非常有意思的结论，进而实现更大的目标，创造出更酷的产品当然，要将一个图的模型，表示成如上图所示，其实很大程度上是数据可视化带来的收益从算法的角度来研究图，还是相对比较枯燥的。

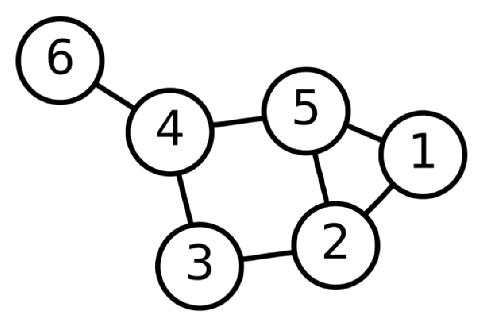
如下，就是一张图：

   

对于图这种数学模型来说，有两个非常重要的组成部分：（1）顶点（Vertex）　　（2）边（Edge）　　其中，顶点和顶点之间就是靠边连接起来的，顶点和边一起构成了一张图。

 

以图作为模型，来表示真实世界之间的关系，那么可以表示什么样的关系呢？从表面上看，这种形式好像很简单，也很枯燥，但是它的内涵却很丰富，如下：

（1）交通运输

最典型的莫过于交通运输，它可以使用图来表达，如：每个顶点可以是一个城市，每条边可以是城市之间的道路再扩展一下，每个顶点可以是一个航站楼，每条边可以是相应的航线，每个顶点可以是港口，每条边可以是相应的海运线甚至更宏观的，每个顶点可以是一个星球，每条边可以是星球之间宇宙飞船飞行的航线，亦或更微观的，每个顶点可以是城市中的一座楼，每条边可以是楼和楼之间的街道。如上，都是可以的，这是对于图来说，最直观的一种表示方式，但是，其实很多更抽象的数据关系，也可以用图来表示。

 

（2）社交网络

对于社交网络来说，每个顶点可以表示一个人，每条边可以表示

人与人之间的关系。这种关系可以是像 FaceBook 这种好友的关

系，也可以是像 Twitter 这种关注的关系。

 

（3）相似关系  

每个顶点可以表示一部电影，每条边可以表示两部电影之间的相似程度

   

（4）互联网

互联网，也可以用图来表示，每个顶点可以表示一个域名，每条边可以表示域名之间的跳转或 每个顶点可以表示一个页面，每条边可以表示页面之间的连接

 

（5）工作安排

在工作中的工作安排，也可以用图来表示，每个顶点可以是一个工作内容，每条边可以是两个工作内容之间的相关程度，或 先后执行的优先级顺序。

 

（6）脑区活动

像脑区活动的研究这样更复杂、更专业的领域，也经常用到图，每个顶点可以是一个脑区，每条边可以是脑区之间信息的传递。

 

（7）程序状态执行

在计算机程序中，程序状态的执行，也可以用图来表示，每个顶点可以表示一个程序状态，每条边可以表示从一种状态执行到另外一种状态。对于这种情况，最典型的一个应用就是自动机，包括制作专业的编译器，甚至是做一个游戏，都可能要设计一个自动机。在这种情况下，或多或少都会使用图论建模的方法。

 

图的分类

使用图可以表示这么多真实世界中不同事物之间的关系，那么在表示的过程中，图也会有一些区别，如下：（1）无向图（Undirected Graph）和有向图（Directed Graph）所谓无向图，即 边是没有方向的，如：在社交网络中，每个顶点表示一个人，人与人之间认识，就连接上一条边，而这个边是没有方向的。

   

所谓有向图，即 边是有方向的，如：在自动机中，每个顶点表示一个事件，每条边表示从一个事件转移到另一个事件，并且这个转移是具有方向性的。

   

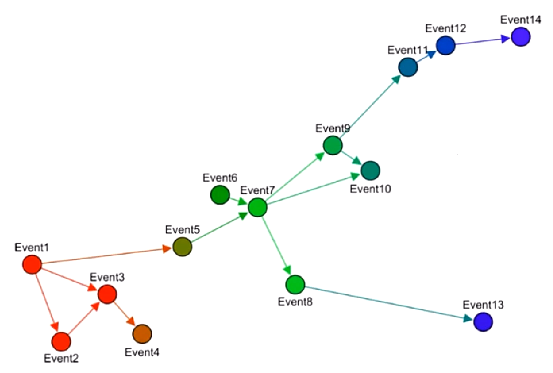
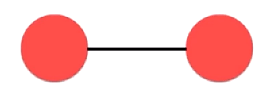
显然，有向图由于其不对称性，所以在很多时候，有向图会涉及到一些相对比较难的算法。其实，无向图可以看做是一种特殊的有向图，如下： 两个顶点之间用一条没有方向的边连接在了一起。

换个角度，可以将一条没有方向的边，换成是两条有方向的边

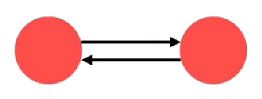
所以说：无向图是一种特殊的有向图

（2）无权图（Unweighted Graph）和有权图（Weighted Graph） 所谓权，可以理解成就是一个数值，而无权和有权，即 连接顶点和顶点之间的边，有没有一个数值和它对应。对于无权图来说，如：在社交网络中，每个顶点表示一个人，每条边表示两个人之间是否认识，即 这条边只表示认识 或不认识的状态存在与否，而不需要有一个值和它联系。

   

而对于有权图来说，如：在交通运输中，每个顶点表示一个地点，每条边表示地点之间的道路。在这种情况下，每条边可能有一个值来表示两个地点之间的距离，或运输费用。

   

 

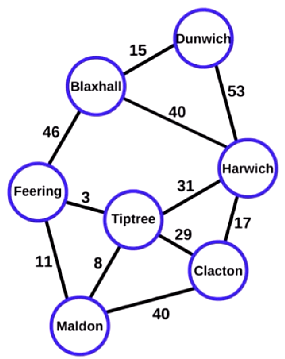
图的连通性

在之前举的例子里，图中的顶点和边全部都连接在了一起，但事实上，作为一个图来说，不一定图中的每一个顶点都要被边连接起来，这就涉及到了图的连通性。如下：

   

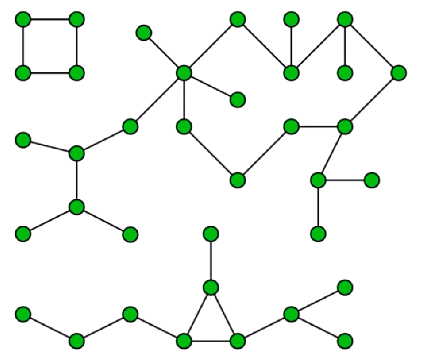
如上所示，它可以是三个图，即 有三个部分，但也可以是一个模型中的一个图，只不过它不是完全连通的，其中有三个连通分量。
 

简单图 

简单图（Simple Graph），即 不含自环边和平行边的图

 

  

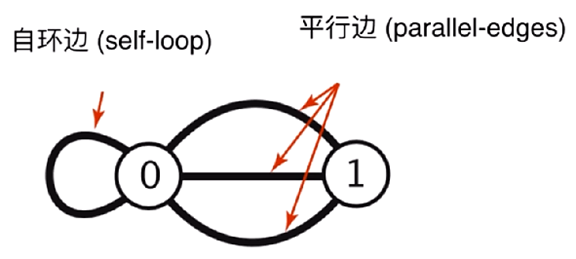
在图论中，存在两种相对比较特殊的边：（1）自环边（self-loop）：一个顶点到这个顶点自身的边　　（2）平行边（parallel-edges）：两个顶点之间存在多条边相连接。无论是自环边还是平行边，在很多时候也是有意义的。最典型的，如：对于交通运输来说，从 A 城市到 B 城市可能有不止一条路，可能有三条路，在这种情况下，平行边就非常有意义 但与此同时，自环边和平行边，会加大算法设计的难度，而且在很多情况下，我们真正关心的问题，其实是和自环边 或 平行边是无关的。最典型的，如：要考察一张图的连通性，那么自环边和平行边都不会改变这张图的连通性。

所以，大多数情况下，讨论的都是简单图