bzoj 1038[ZJOI2008]瞭望塔 - 半平面交

1038: [ZJOI2008]瞭望塔

Time Limit: 10 Sec  Memory Limit: 162 MB

Description

　　致力于建设全国示范和谐小村庄的H村村长dadzhi，决定在村中建立一个瞭望塔，以此加强村中的治安。我们
将H村抽象为一维的轮廓。如下图所示 我们可以用一条山的上方轮廓折线(x1, y1), (x2, y2), …. (xn, yn)来描
述H村的形状，这里x1 < x2 < …< xn。瞭望塔可以建造在[x1, xn]间的任意位置, 但必须满足从瞭望塔的顶端可
以看到H村的任意位置。可见在不同的位置建造瞭望塔，所需要建造的高度是不同的。为了节省开支，dadzhi村长
希望建造的塔高度尽可能小。请你写一个程序，帮助dadzhi村长计算塔的最小高度。

Input

　　第一行包含一个整数n，表示轮廓折线的节点数目。接下来第一行n个整数, 为x1 ~ xn. 第三行n个整数，为y1
 ~ yn。

Output

　　仅包含一个实数，为塔的最小高度，精确到小数点后三位。

Sample Input

【输入样例一】
6
1 2 4 5 6 7
1 2 2 4 2 1
【输入样例二】
4
10 20 49 59
0 10 10 0

Sample Output

【输出样例一】
1.000
【输出样例二】
14.500

HINT

 

 N ≤ 300，输入坐标绝对值不超过106，注意考虑实数误差带来的问题。

 

先把图画出来

 

我们把相邻两点连成直线，然后会发现只要在直线上方就能看到这条线上所有点

而想要满足条件，我们只需要找到这些在最上面的直线（下图所示）

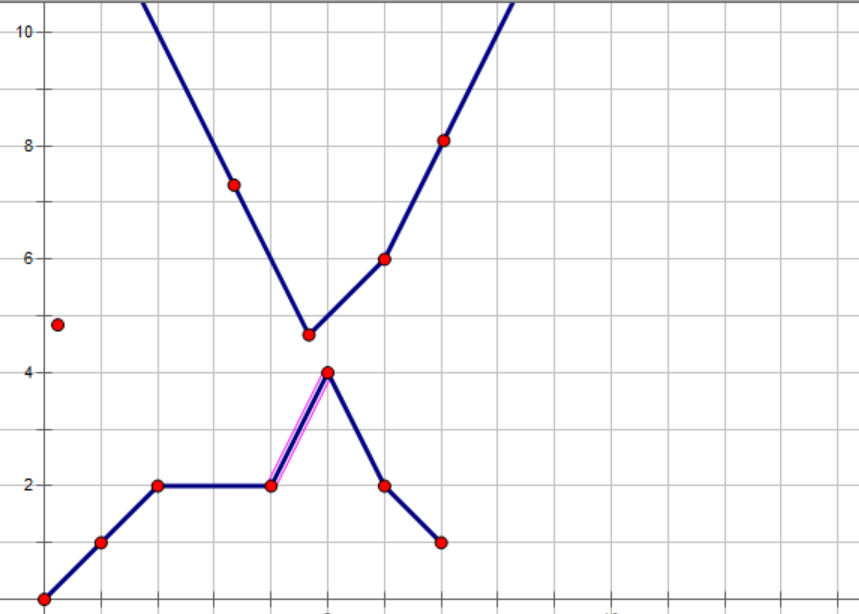
可以发现，这就是一个半凸包，具体求法可以参考——HNOI 2008 水平可见直线

因此我们找出了塔的范围

两条直线间的距离最值肯定在端点处取到， 所以我们从左到右扫一遍

 

HINT

注意上边凸包的交点可能比下面最右边的x要大，直接break掉就好了

 

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 #define LL long long
  6 
  7 using namespace std;
  8 
  9 int top = 0;
 10 double ans;
 11 int s[400];
 12 int N;
 13 struct node {
 14     double x, y;
 15 } n[400];
 16 inline LL read()
 17 {
 18     LL x = 0, w = 1; char ch = 0;
 19     while(ch < '0' || ch > '9') {
 20         if(ch == '-') {
 21             w = -1;
 22         }
 23         ch = getchar();
 24     }
 25     while(ch >= '0' && ch <= '9') {
 26         x = x * 10 + ch - '0';
 27         ch = getchar();
 28     }
 29     return x * w;
 30 }
 31 
 32 struct line {
 33     double k;
 34     double b;
 35 } l[400];
 36 
 37 bool cmp(line a, line b)
 38 {
 39     if(a.k == b.k) {
 40         return a.b > b.b;
 41     }
 42     return a.k < b.k;
 43 }
 44 
 45 double intersaction(int a, int b)
 46 {
 47     return (l[a].b - l[b].b) / (l[b].k - l[a].k);
 48 }
 49 int main()
 50 {
 51     N = read();
 52     for(int i = 1; i <= N; i++) {
 53         n[i].x = read();
 54     }
 55     for(int i = 1; i <= N; i++) {
 56         n[i].y = read();
 57     }
 58     for(int i = 2; i <= N; i++) {
 59         l[i - 1].k = (n[i].y - n[i - 1].y) / (n[i].x - n[i - 1].x);
 60         l[i - 1].b = n[i].y - n[i].x * l[i - 1].k;
 61     }
 62     sort(l + 1, l + N, cmp);
 63     s[0] = 1;
 64     top = 1;
 65     for(int i = 2; i < N; i++) {
 66         if(l[i].k == l[i - 1].k) {
 67             continue;
 68         }
 69         while(top > 1 && intersaction(i, s[top - 1]) <= intersaction(s[top - 1], s[top - 2])) {
 70             top--;
 71         }
 72         s[top++] = i;
 73     }
 74     ans = 1e17;
 75     int t = 1;
 76     for(int i = 0; i < top - 1; i++) {
 77         double x =    intersaction(s[i], s[i + 1]);
 78         while(n[t].x < x && t < N) {
 79             ans = min(ans, l[s[i]].k * n[t].x + l[s[i]].b - n[t].y);
 80             t++;
 81         }
 82         x = min(x, n[N].x);
 83         double kk = (n[t].y - n[t - 1].y) / (n[t].x - n[t - 1].x);
 84         ans = min(ans, l[s[i]].k * x + l[s[i]].b - kk * x - (n[t].y - kk * n[t].x));
 85         if(x == n[N].x) {
 86             break;
 87         }
 88     }
 89     printf("%.3lf\n", ans);
 90     return 0;
 91 }
 92 
 93 /*
 94 6
 95 
 96 1 2 4 5 6 7
 97 
 98 1 2 2 4 2 1
 99 
100 
101 4
102 
103 10 20 49 59
104 
105 0 10 10 0
106 */
View Code

 

posted @ 2018-02-27 16:01  大财主  阅读(150)  评论(0)  编辑  收藏  举报