红黑树操作详解

插入

每次插入后将节点置为红色，这样不会改变路径上黑结点的个数，但是可能存在父亲同为红色的情况。

首先讨论插入到爷爷左子树的情况。

Case1:

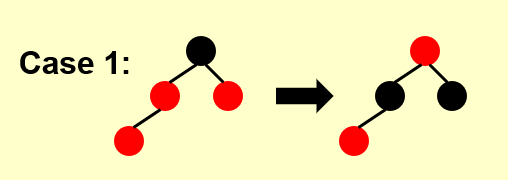
父亲和父亲的兄弟都为红，这时只需要把父亲和爷爷的颜色反转，不会破坏树的性质。

对爷爷进行递归操作。

Case2:

父亲和父亲兄弟的颜色不同稍为麻烦，首先对父亲左旋变为 Case3。

Case3:

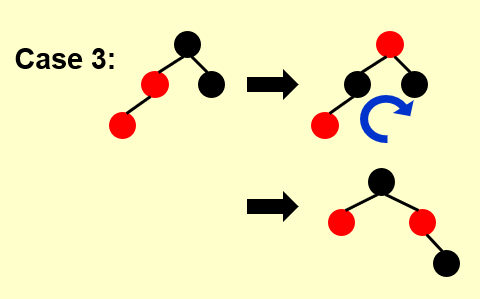
​ 首先将父亲和爷爷的颜色互换，此时颜色的性质满足了，但是路径数量的性质不满足。

​ 所以第二步对爷爷进行 Right Rotate，则满足红黑树的性质。

对称：

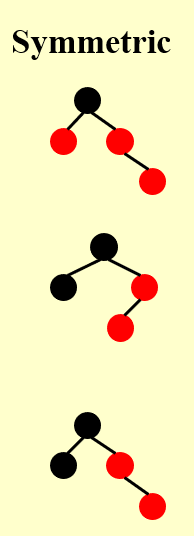
​ 插入到爷爷左子树与插入到爷爷右子树的情况时对称的，同样操作即可。

删除

先执行二叉树搜索树的删除操作，执行后再考虑颜色的修正。

红黑树的删除不同之处在于要记录 x 结点，因为 x 结点(有且仅有)会引起红黑性质的破坏。
同时还要记录 y 结点的颜色， 因为 y 结点被替换会引起黑色变少。

二叉搜索树删除时有三种情况

Case1:

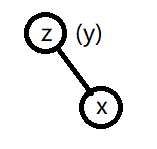
​ Z 只有一个子树， 此时删掉 z, 并把 x 移上去， 因此 z 就是 y。

​ 因为红黑树还连有 nil 结点， 因此叶子结点可以归于Case1。

Case2:

​

​ z 的右儿子就是右子树中最小的结点(选取左右子树都可，我就都对右子树进行操作了)

​ 此时的操作相当于直接把 y 提上去

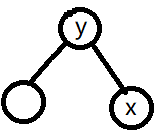
​ 因此我们可以让 y 的 颜色改为 z 的颜色，注意到此时真正颜色性质改变的颜色是原来的 y 结点， 而被 x 替换了。

Case3

​ 这是最后一种二叉搜索树的删除。

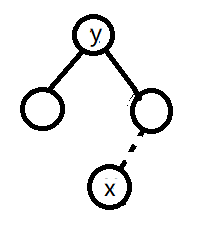
​ 用 y 替换 z, 并将 x 替换到 y 的位置上。

​ 与 Case2 相同，把 y 的颜色改为 z 的颜色，结点性质不变， 只有 y 结点被删掉倒是颜色性质改变。

FIXUP

​ 从上面的删除操作我们发现，只有 y 结点会因为被"删除"且为黑色时可能导致颜色性质被破坏。因此我们只需要对替换 y 的 x 结点进行递归的 FIX 即可。

​ 由于对称性， 下文只讨论 x 为左儿子的情况。

Case1

​ x 为红色或 x 为根， 直接把 x 替换为黑色即可。红变成黑可以满足 y 为黑的性质，且不会破坏原有的性质。

Case2

​ x 的兄弟结点 w 是红色的

​ 此时 x 的父亲一定是黑色的。因此先将 w 和父亲结点的颜色互换。

​ 再对 x 的父亲左旋， 因为 w 的儿子一定是黑色的(w之前是红色)， 所以 x 的兄弟就是黑色，变为 case3,4,5。

Case3

​ x 的兄弟结点 w 是黑色且两个儿子都为黑

​

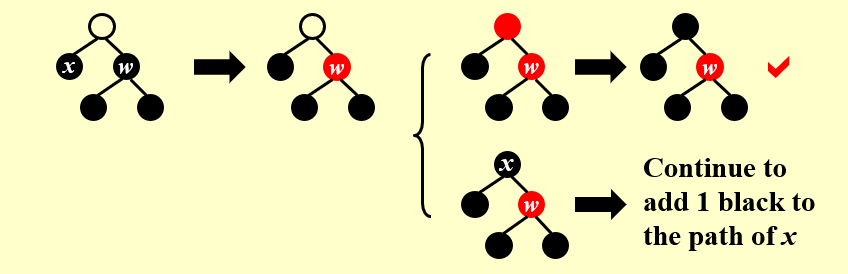
​ 此时直接将 w 变为红色， 再把 x 的父亲变为黑色，可视为新的 x， 递归讨论即可。
书上将 x 称为双重黑色，即原来 y 的黑色叠加到 x 上， 此时把 x 的黑色叠加到父亲上也可以这样理解。

Case4

​ x 的兄弟结点 w 是黑色， 左孩子是红色， 右孩子是黑色

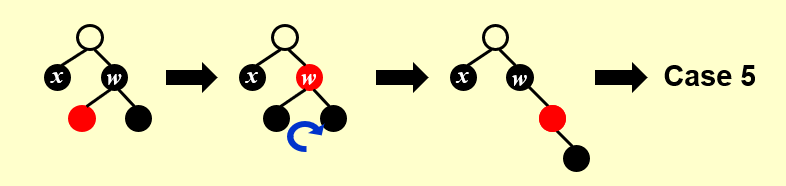
​ 先将 w 与左儿子颜色互换， 再对 w 右旋，即变为 Case5。

Case5

​ x 的兄弟结点 w 是黑色， 右孩子是红色

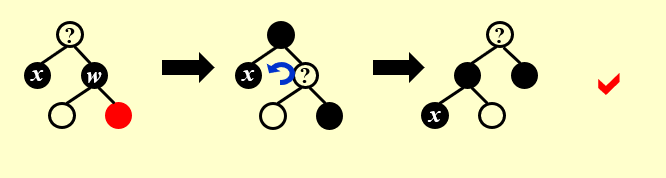
​ 这步操作相当于把 x 的其中一个黑色分给了 w 的右儿子， 再将 w 和 父亲颜色互换，最后对父亲进行左旋。

​ 这个过程不会破坏红黑树的性质(挖坑，证明略)，因此只需要将根设为 x 递归向上处理即可