郑捷《机器学习算法原理与编程实践》学习笔记（第五章 梯度寻优）5.2 Logistic梯度下降法

　　5.2.1 梯度下降（略）

　　5.2.2 线性分类器（略）

　　5.2.3 Logistic函数—世界不是非黑即白

　　5.2.4 算法流程

　　单神经元的Logistic分类器

　　（1）导入数据

　　

#coding:utf-8
import sys
import os
from numpy import *

#配置UTF-8的输出环境
reload(sys)
sys.setdefaultencoding('utf-8')

#数据文件转矩阵
#path：数据文件路径
#delimiter：行内字段分隔符
def file2matrix(path,delimiter):
    recordlist = []
    fp         = open(path,"rb")#读取文件内容
    content    = fp.read()
    fp.close()
    rowlist    = content.splitlines()#按行转化为一维表
    #逐行遍历，结果按分割符分割为行向量
    recordlist = [map(eval,row.split(delimiter)) for row in rowlist if row.strip()] #eval字符串str当成有效的表达式来求值并返回计算结果
    return  mat(recordlist)#返回转换后的矩阵形式

Input  = file2matrix("testSet.txt","\t") #导入数据并转换为矩阵
target = Input[:,-1]                       #获取分类的标签数据
(m,n)  = shape(Input)

　　（2）按分类绘制散点图

　　

def drawScatterbyLabel(plt,Input):
    (m,n)  = shape(Input)
    target = Input[:,-1]
    for i in xrange(m):
        if target[i] == 0:
            plt.scatter(Input[i,0],Input[i,1],c='blue',marker = 'o')
        else:
            plt.scatter(Input[i,0],Input[i,1],c = 'red',marker = 's')
    plt.show()

 

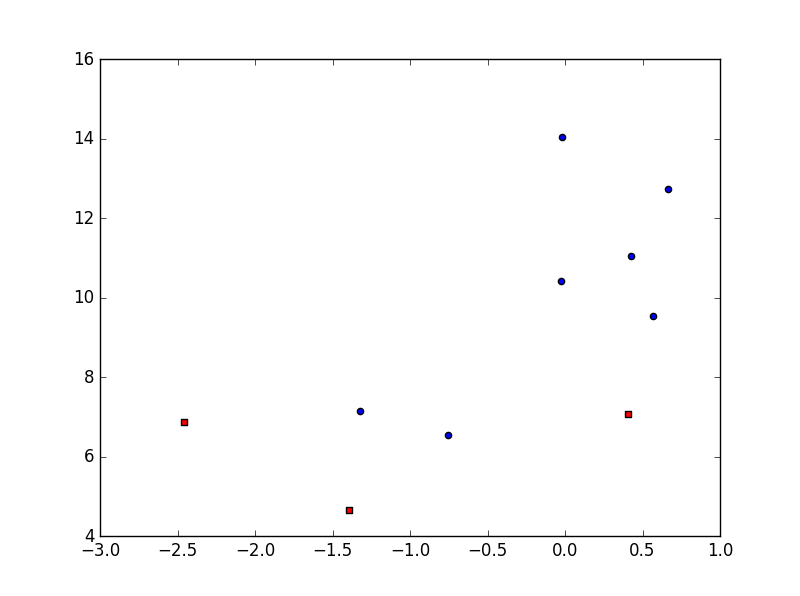
 　　（3）构建b+x系数矩阵：b这里默认为1

　

def buildMat(dataSet):
    m,n     = shape(dataSet)
    dataMat = zeros((m,n))
    dataMat[:,0]  = 1               #矩阵的第一列全部设置为1
    dataMat[:,1:] = dataSet[:,:-1]  #第一列和倒数第二列保持源数据不变，删除最后一列
    return dataMat

 　　结果为：

　　[[  1.        -0.017612  14.053064]
 　　[  1.        -1.395634   4.662541]
 　　[  1.        -0.752157   6.53862 ]
　　 [  1.        -1.322371   7.152853]
 　　[  1.         0.423363  11.054677]
 　　[  1.         0.406704   7.067335]
 　　[  1.         0.667394  12.741452]
 　　[  1.        -2.46015    6.866805]
 　　[  1.         0.569411   9.548755]
　　 [  1.        -0.026632  10.427743]]

　　（4）定义步长和迭代次数，并初始化权重向量

alpha = 0.001                       #步长
steps = 500                         #迭代次数
weight = ones((n,1))                #初始化权重向量

　　（5）主程序：迭代过程

def logistic(wTx):
    return 1.0/(1.0+exp(-wTx))

for k in xrange(steps):
    gradient = dataMat*mat(weight)  #计算梯度
    output   = logistic(gradient)   #Logistic函数
    errors   = target - output      #计算误差
    weights  = weights + alpha*dataMat.T*errors #修正误差，进行迭代

输出权重：

[[ 1.20770866]
 [-0.13220832]
 [-0.28097863]]

 　　（6）绘制分类超平面

　　

X = np.linspace(-5,5,100)
#y = w*x+b:b:weight[0]/weight[2];w:weights[1]/weight[2]
Y = -(double(weights[0])+X*(double(weights[1])))/double(weights[2])
plt.plot(X,X)
plt.show()

　　5.2.5 对测试集进行分类

　　（1）分类器函数

　　

def classifier(testData,weights):
    prob = logistic(sum(testData*weights))  #求取概率-判别算法
    if prob > 0.5:
        return 1.0
    else:
        return 0.0

　　（2）对测试数据执行分类

　　

def classifier(testData,weights):
    prob = logistic(sum(testData*weights))  #求取概率-判别算法
    if prob > 0.5:
        return 1.0
    else:
        return 0.0


weights = mat([[ 1.20770866],[-0.13220832],[-0.28097863]])  #载入之前生成的权重
testdata = mat([-0.147324,2.874846])                        #测试数据
m,n      = shape(testdata)                                  #构建测试数据矩阵
testmat  = zeros((m,n+1))
testmat[:,0] = 1
testmat[:,1:] = testdata
print classifier(testmat,weights)

输出结果：1

参考资料： 郑捷《机器学习算法原理与编程实践》  仅供学习研究