郑捷《机器学习算法原理与编程实践》学习笔记(第一章 机器学习基础)
第一章 机器学习的基础
1.1编程语言与开发环境
1.1.1 Python 安装(略)
1.2.2 Python安装包的安装:可以选选择安装集成包anaconda(略)
1.1.3 IDE配置及安装测试
IDE选择UltraEdit高级文本编辑器,配置步骤如下:
(1)选择“高级”-->“用户工具”命令,如图1.4所示。

图1.5 配置UltraEdit步骤1
(2)在如图1.5所示输入各项参数,然后单击“应用按钮”
图1.5 配置UltraEdit步骤2
(3)按照如图1.6所示进行设置,然后单击“确定”按钮
图1.6 配置UltraEdit步骤3
通过测试代码,检验安装效果:
#coding:utf-8 #Filename:mytest1.py import numpy as np #导入NumPy库 from numpy import * #导入NumPy库 import matplotlib.pyplot as plt #测试数据集————二维list dataSet = [[1,2],[3,4],[5,6],[7,8],[9,10]] dataMat = mat(dataSet).T #将数据集转换为NumPy矩阵,并转秩 plt.scatter(dataMat[0],dataMat[1],c = 'red',marker = 'o') #绘制数据散点图 #绘制直线图形 X = np.linspace(-2,2,100) #产生直线数据 #建立线性方程 Y = 2.8*X+9 plt.plot(X,Y) #绘制直线图 plt.show() #显示绘制效果
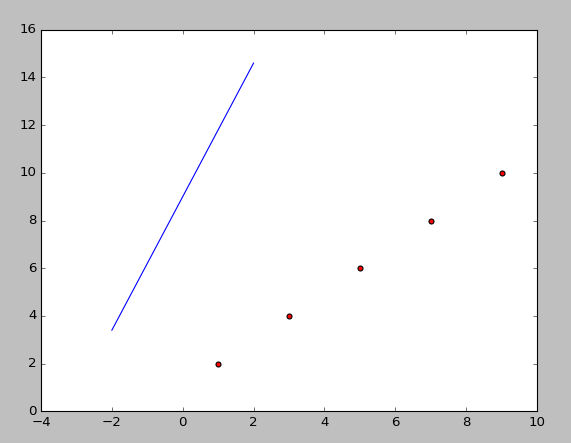
图1.7 显示执行效果
1.2 对象、矩阵与矢量化编程
1.2.1对象与维度(略)
1.2.2初识矩阵(略)
1.2.3矢量化编程与GPU运算(略)
1.2.4理解数学公式与NumPy矩阵运算
1.矩阵的初始化
#coding:utf-8
import numpy as np #导入NumPy包
#创建3*5的全0矩阵和全1的矩阵
myZero = np.zeros([3,5])#3*5的全0矩阵
print myZero
myZero = np.ones([3,5])##3*5的全1矩阵
print myZero
输出结果:
Connected to pydev debugger (build 141.1580)
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
[[ 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1.]]
#生成随机矩阵
myRand = np.random.rand(3,4)#3行4列的0~1之间的随机数矩阵
print myRand
输出结果如下:
[[ 0.14689327 0.15077077 0.88018968 0.75112348]
[ 0.30944489 0.77563281 0.82905038 0.25430367]
[ 0.53958541 0.89695376 0.90681161 0.25453046]]
#单位阵
myEye = np.eye(3)#3*3的矩阵
print myEye
输出结果如下:
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
2.矩阵的元素运算
矩阵的元素运算是指矩阵在元素级别的加减乘除运算。
#元素的加和减:条件是矩阵的行数和列数必须相同
from numpy import *#导入NumPy包
myOnes = ones([3,3])#3*3的全1矩阵
myEye = eye(3)
print myOnes+myEye
print myOnes-myEye
输出结果如下:
[[ 2. 1. 1.]
[ 1. 2. 1.]
[ 1. 1. 2.]]
[[ 0. 1. 1.]
[ 1. 0. 1.]
[ 1. 1. 0.]]
#矩阵乘法
mymatrix = mat([[1,2,3],[4,5,6],[7,8,9]])
a = 10
print a*mymatrix
输出结果:
[[10 20 30]
[40 50 60]
[70 80 90]]
#矩阵所有元素求和
mymatrix = mat([[1,2,3],[4,5,6],[7,8,9]])
print mymatrix.sum()
输出结果:
45
'''
矩阵各元素的积:矩阵的点乘同维对应元素的相乘。
当矩阵的维度不同时,会根据一定的广播将维数扩
充到一致的形式
'''
mymatrix1 = mat([[1,2,3],[4,5,6],[7,8,9]])
mymatrix2 = 1.5*ones([3,3])
print multiply(mymatrix1,mymatrix2)
输出结果:
[[ 1.5 3. 4.5]
[ 6. 7.5 9. ]
[ 10.5 12. 13.5]]
#矩阵各元素的n次幂:n=2
mymatrix1 = mat([[1,2,3],[4,5,6],[7,8,9]])
print power(mymatrix1,2)
输出结果:
[[ 1 4 9]
[16 25 36]
[49 64 81]]
#矩阵乘以矩阵
mymatrix1 = mat([[1,2,3],[4,5,6],[7,8,9]])
mymatrix2 = mat([[1],[2],[3]])
print mymatrix1*mymatrix2
输出结果:
[[14]
[32]
[50]]
#矩阵的转置
mymatrix1 = mat([[1,2,3],[4,5,6],[7,8,9]])
print mymatrix1.T #矩阵的转置
mymatrix1.transpose() #矩阵的转置
print mymatrix1
输出结果如下:
[[1 4 7]
[2 5 8]
[3 6 9]]
[[1 2 3]
[4 5 6]
[7 8 9]]
mymatrix = mymatrix1[0]#按行切片
print u"按行切片:",mymatrix
mymatrix = mymatrix1.T[0]#按列切片
print u"按列切片:",mymatrix
mymatrix = mymatrix1.copy()#矩阵的复制
print u"复制矩阵:",mymatrix
#比较
print u"矩阵元素的比较:\n",mymatrix<mymatrix1.T
输出结果:
矩阵的行数和列数: 3 3
按行切片: [[1 2 3]]
按列切片: [[1 4 7]]
复制矩阵: [[1 2 3]
[4 5 6]
[7 8 9]]
矩阵元素的比较:
[[False True True]
[False False True]
[False False False]]
1.2.5 Linalg线性代数库
在矩阵的基本运算基础之上,NumPy的Linalg库可以满足大多数的线性代数运算。
.矩阵的行列式
.矩阵的逆
.矩阵的对称
.矩阵的秩
.可逆矩阵求解线性方程
1.矩阵的行列式
In [4]: from numpy import *
In [5]: #n阶矩阵的行列式运算
In [6]: A = mat([[1,2,3],[4,5,6],[7,8,9]])
In [7]: print "det(A):",linalg.det(A)
det(A): 6.66133814775e-16
2.矩阵的逆
In [8]: from numpy import *
In [9]: A = mat([[1,2,3],[4,5,6],[7,8,9]])
In [10]: invA = linalg.inv(A)#矩阵的逆
In [11]: print "inv(A):",invA
inv(A): [[ -4.50359963e+15 9.00719925e+15 -4.50359963e+15]
[ 9.00719925e+15 -1.80143985e+16 9.00719925e+15]
[ -4.50359963e+15 9.00719925e+15 -4.50359963e+15]]
3.矩阵的对称
In [12]: from numpy import *
In [13]: A = mat([[1,2,3],[4,5,6],[7,8,9]])
In [14]: AT= A.T
In [15]: print A*AT
[[ 14 32 50]
[ 32 77 122]
[ 50 122 194]]
4.矩阵的秩
In [16]: from numpy import *
In [17]: A = mat([[1,2,3],[4,5,6],[7,8,9]])
In [18]: print linalg.matrix_rank(A)#矩阵的秩
2
5.可逆矩阵求解
1.3 机器学习的数学基础
1.3.1 相似度的度量
范数(来自百度百科):向量的范数可以简单、形象的理解为长度,或者向量到坐标系原点的距离,或者相应空间内两点之间的距离。
向量的范数定义:向量的范数是一个函数||x||,满足非负性||x||≥0,齐次性||cx|| = |c| ||x||,三角不等式||x+y||≤||x||+||y||。
L1范数:||x||为x向量各个元素绝对值之和
L2范数:||x||为x向量各个元素的平方和的开方。L2范数又称Euclidean范数或者Frobenius范数
Lp范数:||x||为x向量各个元素绝对值p次方和的1/p次方。
L∞范数:||x||为x向量各个元素绝对值最大的元素,如下:
向量范数的运算如下:
In [27]: A = [8,1,6]
In [28]: #手工计算
In [29]: modA = sqrt(sum(power(A,2)))
In [30]: #库函数
In [31]: normA = linalg.norm(A)
In [32]: print "modA:",modA,"norm(A):",normA
modA: 10.0498756211 norm(A): 10.0498756211
1.3.2 各类距离的意义与Python代码的实现 本小节所列的距离公式列表和代码如下:
•闵可夫斯基距离(Minkowski Distance)
•欧式距离(Euclidean Distance)
•曼哈顿距离(Manhattan Distance)
•切比雪夫距离(Chebyshev Distance)
•夹角余弦(Cosine)
•汉明距离(Hamming Distance)
•杰卡德相似系数(Jaccard Similiarity Coeffcient)
1. 闵可夫斯基距离(Minkowski Distance)
严格意义上讲,闵可夫斯基距离不是一种距离,而是一组距离的定义。
两个n维变量A(x11,x12,...,x1n)与B(x21,x22,...,x2n)间的闵可夫斯基距离定义为:
其中p是一个变参数
•当p=1时,就是曼哈顿距离
•当p=2时,就是欧式距离
•当p=∞时,就是切比雪夫距离
根据变参数的不同,闵可供夫斯基可以表示一类的距离
2.欧式距离(Euclidean Distance)
欧氏距离(L2范数)是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式,如图所示
(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧式距离
(2)三维空间两点A(x1,y1,z1)与B(x2,y2,z2)
(3) 两个n维向量A(x11,x12,...,x1n)与B(x21,x22,...,x2n)间的欧氏距离:
(4)Python实现欧式距离
In [33]: from numpy import *
In [34]: vector1 = mat([1,2,3])
In [35]: vector2 = mat([4,5,6])
In [36]: print sqrt((vector1-vector2)*((vector1-vector2).T))
[[ 5.19615242]]
3.曼哈顿距离(Manhattan Distance)
(1)二维平面两点A(x1,y1)与B(x2,y2)间的曼哈顿距离:
(2)两个n维向量A(x11,x12,...,x1n)与B(x21,x22,...,x2n)间的曼哈顿距离
(3)Python实现曼哈顿
In [1]: from numpy import *
In [2]: vector1 = mat([1,2,3])
In [3]: vector2 = mat([4,5,6])
In [4]: print sum(abs(vector1-vector2))
9
4、切比雪夫距离(Chebyshev Distance)

(1)二维平面两点A(x1,y1)与B(x2,y2)间的切比雪夫距离:
(2)两个n维平面两点A(x11,y12,..,x1n)与B(x21,y22,..,x2n)间的切比雪夫距离:
这个公式的另外一种等价形式是:
(3)Python实现切比雪夫距离。
In [1]: from numpy import *
In [2]: vector1 = mat([1,2,3])
In [3]: vector2 = mat([4,7,5])
In [4]: print abs(vector1-vector2).max()
5
5.夹角余弦(Consine)
几何中的夹角余弦可用来衡量两个向量方向的差异

(1)二维平面两点A(x1,y1)与B(x2,y2)间的夹角余弦公式:
(2)两个n维样本点A(x11,x12,x13,...,x1n)与B(x21,x22,...,x2n)的夹角余弦:
即:
夹角余弦取值范围为[-1,1]。夹角余弦越大,表示向量的夹角越小;夹角余弦越小,表示两个向量的夹角越大。当两个向量的方向重合时,夹角余弦取最大值1;当两个向量的方向完全相反时,夹角余弦取值最小值-1.
(3)Python实现夹角余弦
In [7]: from numpy import *
In [8]: vector1 = mat([1,2,3])
In [9]: vector2 = mat([4,7,5])
In [10]: cosV12 = dot(vector1,vector2.T)/(linalg.norm(vector1)*linalg.norm(vector2))
In [11]: print cosV12
[[ 0.92966968]]
6.汉明距离(Hamming Distance)
(1)汉明距离的定义:两个等长的字符串s1和s2之间的汉明距离定义为将其中一个变为另外一个所需要的最小替换次数。例如字符串“111“与“1001”之间的汉明距离为2.
应用:信息编码(为了增强容错性,应使编码间的最小汉明距离尽可能大)。
(2)使用Python实现汉明距离。
In [20]: from numpy import *
In [21]: matV = mat([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]])
In [22]: smstr = nonzero(matV[0]-matV[1])
In [23]: smstr
Out[23]:
(array([0, 0, 0, 0, 0, 0], dtype=int64),
array([0, 2, 3, 5, 6, 7], dtype=int64))
In [24]: print shape(smstr[0])
(6L,)
7.杰卡德相似系数(Jaccard Similarity Coefficient)
(1)杰卡德相似系数:两个集合A和B的交集元素在A、B的并集中所占的比例,成为两个集合的杰卡德相似系数,用符号J(A,B)表示。
杰卡德相似系数是衡量两个集合的相似度的一种指标。
(2)杰卡德距离:与杰卡德相似系数相反的概念是杰卡德距离(Jaccard Distance),杰卡德距离可用如下的公式表示:
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度
(3)杰卡德相似系数与杰卡德距离的应用。
可将杰卡德相似系数用在衡量样本的相似度上。
样本A与样本B是两个n维向量,而且所有维度上的取值都是0或者1.例如,A(0111)和B(1011)。我们将样本看成一个集合,1表示该集合包含该元素,0表示集合不包含该元素。
P:样本A与B都是1的维度的个数
q:样本A是1、样本B是0的维度的个数
r: 样本A是0、样本B是1的维度的个数
s:样本A与B都是0的维度的个数
那么样本A与B的杰卡德相似系数可以表示为:

这里p+q+r可以理解为A与B的并集的元素个数,而p是A与B的交集的元素个数。
(4)Python实现杰卡德距离。
In [25]: from numpy import *
In [26]: import scipy.spatial.distance as dist #导入Scipy距离公式
In [27]: matV = mat([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]])
In [28]: print "dist.jaccard:",dist.pdist(matV,'jaccard')
dist.jaccard: [ 0.75]
1.3.3理解随机性(略)
1.3.4回顾概率论(略)
1.3.5多元统计基础(略)
1.3.6特征相关性
1.相关系数
(1)相关系数定义:
(2)相关距离定义:

(3)Python实现相关系数
In [13]: from numpy import * In [14]: matV = mat([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]]) ...: In [15]: mv1 = mean(matV[0])#第一列的均值 In [16]: mv2 = mean(matV[1])#第二列的均值 In [17]: #计算两列的标准差 In [18]: dv1 = std(matV[0]) In [19]: dv2 = std(matV[1]) In [20]: corref = mean(multiply(matV[0]-mv1,matV[1]-mv2))/(dv1*dv2) In [21]: print corref
2马氏距离
(1)马氏距离的定义:有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到μ的距离为:
而其中xi与Xj之间的马氏距离为:
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式变成欧式距离公式:

若协方差是对角矩阵,则公式变成可标准化的欧式距离公式
(2)马氏距离的优点:量纲无关,排除变量之间的相关性的干扰。
(3)马氏距离的Python计算:
In [49]: from numpy import * In [50]: matV = mat([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]]) In [51]: covinv = linalg.inv(cov(matV)) In [52]: tp =matV.T[0]-matV.T[1] In [53]: distma = sqrt(dot(dot(tp,coninv),tp.T)) In [54]: distma = sqrt(dot(dot(tp,covinv),tp.T)) In [55]: distma Out[55]: matrix([[ 2.02547873]])
1.3.7 再谈矩阵-空间的变换(略)
5.特征值和特征向量
python求取矩阵的特征值和特征向量。
In [56]: A = [[8,1,6],[3,5,7],[4,9,2]] In [57]: evals,evecs = linalg.eig(A) In [58]: print '特征值:',evals,'\n特征向量:',evecs 特征值: [ 15. 4.89897949 -4.89897949] 特征向量: [[-0.57735027 -0.81305253 -0.34164801] [-0.57735027 0.47140452 -0.47140452] [-0.57735027 0.34164801 0.81305253]]
1.3.8 数据的归一化
2.欧式距离标准化:
X* = (X-M)/S
标准化的后的值 = (标准化前的值-分量的均值)/分量的标准差
两个n维向量的之间的标准化的欧式距离公式:

标准化欧式距离Python的实现
In [2]: from numpy import * In [3]: vectormat = mat([[1,2,3],[4,5,6]]) In [4]: v12 = vectormat[0]-vectormat[1] In [5]: print sqrt(v12*v12.T) [[ 5.19615242]] In [6]: #norm In [7]: varmat = std(vectormat.T,axis=0) In [16]: normvmat =(vectormat-mean(vectormat))/varmat.T In [17]: normv12 =normvmat[0]-normvmat[1] In [18]: sqrt( normv12* normv12.T) Out[18]: matrix([[ 8.5732141]])
1.4 数据处理和可视化
1.4.1 数据的导入和内存管理
1.数据表文件的读取
Python读取数据表例程:
#coding:utf-8 import sys import os from numpy import * #配置UTF-8的输出环境 reload(sys) sys.setdefaultencoding('utf-8') #数据文件转矩阵 #path:数据文件路径 #delimiter:行内字段分隔符 def file2matrix(path,delimiter): recordlist = [] fp = open(path,"rb")#读取文件内容 content = fp.read() fp.close() rowlist = content.splitlines()#按行转化为一维表 #逐行遍历,结果按分割符分割为行向量 recordlist = [map(eval,row.split(delimiter)) for row in rowlist if row.strip()] return mat(recordlist)#返回转换后的矩阵形式 root = "testdata" #数据文件所在路径 pathlist = os.listdir(root) for path in pathlist: recordmat = file2matrix(root + "/"+path," ")#文件到矩阵的转换 print shape(recordmat)
2.对象的持久化
有时候,我们希望数据以对象的方式保存。Pytho提供了cPickle模块支持对象的读写
#继续上面的代码 import cPickle as pickle #导入序列化库 file_obj = open(root +"/recordmat.dat","wb") pickle.dump(recordmat[0],file_obj)#强生成的矩阵对象保存到指定的位置 file_obj.close() #c此段代码可将刚才转换为矩阵的数据持久化为对象的文件 #读取序列化后的文件 read_obj = open(root+"/recordmat.dat","rb") readmat = pickle.load(read_obj) #从指定的位置读取对象 print shape(readmat)
3.高效的读取大文本的文件
#按行读取文件,读取指定的行数:nmax = 0 按行读取全部 def readfilelines(path,nmax = 0): fp = open(path,"rb") ncount = 0 #读取行 while True: content = fp.readline() if content == "" or (ncount>=nmax and nmax !=0):#判断文件尾或读完指定行数 break yield content#返回读取的行 if nmax != 0: ncount += 1 fp.close() root = "testdata/01.txt" #数据文件所在路径 for line in readfilelines(path,nmax=10):#读取10行 print line.strip()
1.4.2 表与线性结构的可视化
示例代码:
In [1]: import numpy as np In [2]: import matplotlib.pyplot as plt In [3]: #曲线数据加入噪声 In [4]: x = np.linspace(-5,5,200) In [5]: y = np.sin(x) #给出y与x的基本关系 In [6]: yn = y+np.random.rand(1,len(y))*1.5#加入噪声的点集 In [7]: #绘图 In [8]: fig = plt.figure() In [9]: ax = fig.add_subplot(1,1,1) In [10]: ax.scatter(x,yn,c='blue',marker='o') Out[10]: <matplotlib.collections.PathCollection at 0x6b7f780> In [11]: ax.plot(x,y+0.75,'r') Out[11]: [<matplotlib.lines.Line2D at 0x6d510f0>] In [12]: plt.show()
1.4.3 树与分类结构的可视化(略)
1.4.4 图与网格结构的可视化(略)
资料来源及版权所有:《机器学习算法原理与编程实践》郑捷



