排序算法
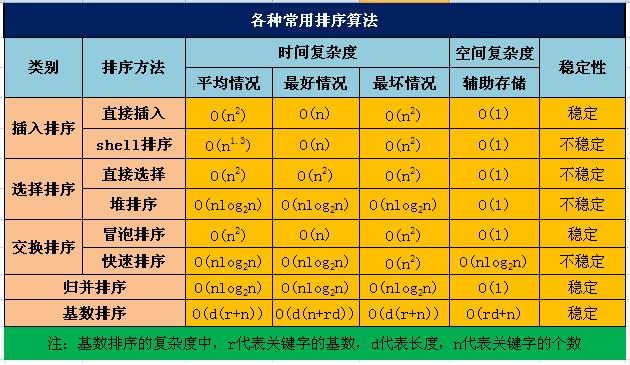
几种排序算法的比较
直接插入排序
算法
插入排序由N-1趟排序组成。对于p=1到N-1趟,插入排序保证从位置0到位置p上的元素为已排序状态。
时间复杂度
最差的情况下,第p次排序,需要的比较次数是p次,则总的比较次数为1+2+3+……+N-1=O(N^2)。
平均情况,O(N^2)
最好情况,O(N)
空间复杂度
每次比较都是两个元素的交换,所以空间复杂度为O(1)
代码示例
package sort;
import java.util.Random;
/**
* Created by wuchao on 17-3-28.
*/
public class Insert {
public static void main(String[] args){
int[] array = getData(100);
printArray(insertSort(array));
}
//插入排序
public static int[] insertSort(int[] array){
int N = array.length;
int j;
for(int i=1 ; i<N ; i++){
//array[0,(i-1)]是已经排序的,现在判断array[i]插在哪
int tmp = array[i];
for(j=i;j>0&&array[j-1]<tmp;j--){
array[j]=array[j-1];
}
array[j]=tmp;
}
return array;
}
//返回一个长度为N的随机数组,元素大小[0,N]
public static int[] getData(int N){
int[] array = new int[N];
if(N<=0) return array;
Random random = new Random();
for(int i=0;i<N;i++){
array[i]= random.nextInt(N);
}
return array;
}
//打印数组
public static void printArray(int[] array){
System.out.print("[");
for(int i=0;i<array.length;i++){
System.out.print(array[i]+",");
}
System.out.print("]");
System.out.println();
}
}
Shell排序
算法
基于插入排序,但它通过比较相邻一定间隔的元素来工作。各趟比较所用的距离随着算法进行而减少,直到只比较相邻元素(间隔为1)的最后一趟为止。
时间复杂度
最差情况,O(N^2)
平均情况,O(N^1.3)
最好情况,O(N)
空间复杂度
每次比较都是两个元素的交换,所以空间复杂度为O(1)
代码示例
package sort;
import java.util.Random;
/**
* Created by wuchao on 17-3-28.
*/
public class Shell {
public static void main(String[] args){
int[] array = getData(100);
printArray(array);
printArray(shellSort(array));
}
//shell排序
public static int[] shellSort(int[] array){
int N = array.length;
int j;
//比较间隔gap由N/2逐步递减为1
for(int gap = N/2;gap>0;gap/=2){
for(int i=gap;i<N;i++){
int tmp = array[i];
for(j=i;j>=gap&&array[j-gap]>tmp;j -=gap){
array[j]=array[j-gap];
}
array[j]=tmp;
}
}
return array;
}
//返回一个长度为N的随机数组,元素大小[0,N]
public static int[] getData(int N){
int[] array = new int[N];
if(N<=0) return array;
Random random = new Random();
for(int i=0;i<N;i++){
array[i]= random.nextInt(N);
}
return array;
}
//打印数组
public static void printArray(int[] array){
System.out.print("[");
for(int i=0;i<array.length;i++){
System.out.print(array[i]+",");
}
System.out.print("]");
System.out.println();
}
}
快速排序
算法
在数组中选取一个元素,比如选第一个元素,经过一定的方法,使得数组重排,结果为比该元素小的元素都在该元素的左侧,比该元素大的元素都在该元素的右侧。
重排方法如下:
数组为array=[5 2 7 3 9 4 0 1]
(1)选取第一个元素为基x=5,相当于在array[i=0]处挖了一个坑,元素被取走了。
(2)建立索引i=0,j=6(i指向数组头部,j指向数组尾部),此时i=0指向数组的那个坑
(3)从尾部开始查找第一个小于x的值(查找范围为(i,j] ),然后令j指向该元素,并将该元素赋值数组的那个坑并i++(i指向的那个坑),此时j指向数组的新的坑
(4)从头部开始查找第一个大于x的值(查找范围[i,j) ),然后令i指向该元素,并将该元素复制给数组的那个坑并j--(j指向的坑),此时i指向数组新的坑
(5)直到i<j不成立时有i=j,这时坑的位置是i或j,用基x填这个坑,array[i]=x;
数组[5 2 7 3 9 4 0 1]排序细节如下
[ _ 2 7 3 9 4 0 1 ] x=5 i=0,j=7
[ 1 2 7 3 9 4 0 _ ] x=5 i=0,j=7
[ 1 2 _ 3 9 4 0 7 ] x=5 i=2,j=7
[ 1 2 0 3 9 4 _ 7 ] x=5 i=2,j=6
[ 1 2 0 3 _ 4 9 7 ] x=5 i=4,j=6
[ 1 2 0 3 4 _ 9 7 ] x=5 i=4,j=5
[ 1 2 0 3 4 5 9 7 ] x=5 i=5,j=5
时间复杂度
最差情况:O(n^2)
平均情况:O(nlogn)
空间复杂度
O(nlogn)
代码
代码如下
/**
* Created by wuchao on 17-3-29.
*/
import java.util.*;
public class test {
public static int array[] = {5,2,7,1,2,9,3};
public static void main(String[] args) {
quickSort(array,0,6);
System.out.println(Arrays.toString(array));
}
public static void quickSort(int[] array,int l,int r){
if(l<r){
int i=l,j=r;
int value = array[l];
while(i<j){
while(i<j && array[j]>value){
j--;
}
if(i<j){
array[i]=array[j];
i++;
}
while(i<j&&array[i]<value){
i++;
}
if(i<j){
array[j]=array[i];
j--;
}
}
array[i]=value;
quickSort(array,l,i-1);
quickSort(array,i+1,r);
}
}
}
归并排序
算法
这个算法的基本操作是合并两个已排序的表。在这里合并函数的几个参数a,tmpArray,leftPos,rightPos,rightEnd分别表示待排序数组、临时数组、左边起点、右边起点、右边终点。
时间复杂度
最差和最好情况下都是O(nlogn)
空间复杂度
O(1)
代码
import java.util.Arrays;
/**
* 归并排序
*/
public class Merge {
public static void main(String[] args){
int[] array={2,7,3,77,3,56,3,74,2,5,12,74,34,75};
mergeSort(array);
System.out.println(Arrays.toString(array));
}
//排序算法入口
public static void mergeSort(int[] a){
int[] tmpArray = new int[a.length];
mergeSort(a,tmpArray,0,a.length-1);
}
//分治并合并
private static void mergeSort(int[] a,int[] tmpArray,int left,int right){
if(left<right){
int middle = (left+right)/2;
mergeSort(a,tmpArray,left,middle);
mergeSort(a,tmpArray,middle+1,right);
merge(a,tmpArray,left,middle+1,right);
}
}
//合并
//此时数组a的[leftPos]-[rightPos-1]和[rightPos]-[rightEnd]已经是两个排序的子数组
//下面函数负责将这两个部分合并,并放入放到tmpArray数组的[leftPos]-[rightEnd]位置
//最后将tmpArray对应部分拷贝回原来数组
private static void merge(int[] a,int[] tmpArray,int leftPos,int rightPos,int rightEnd){
int leftEnd = rightPos-1;
int tmpPos = leftPos;
int numElements = rightEnd-leftPos+1;
while(leftPos<=leftEnd && rightPos<=rightEnd){
if(a[leftPos]<=a[rightPos]){
tmpArray[tmpPos++]=a[leftPos++];
}else{
tmpArray[tmpPos++]=a[rightPos++];
}
}
while(leftPos<=leftEnd){
tmpArray[tmpPos++]=a[leftPos++];
}
while(rightPos<=rightEnd){
tmpArray[tmpPos++]=a[rightPos++];
}
for(int i=0;i<numElements;i++,rightEnd--){
a[rightEnd]=tmpArray[rightEnd];
}
}
}


