第五章支持向量机

边界：感知

在逻辑回归中，$p(y=1 \mid x;\theta)$的概率由$h_{\theta}(x)=g(\theta^{T}x)$建立模型。当$h_{\theta}(x)\geq 0.5$则预测x的输出为1。或者说当$\theta_{x} \geq 0$则预测x的输出为1。因此当$\theta_{x} \gg 0$时，我们认为准确预测输出为1。

如上图，点A可以准确预测为x，而C点距离判决边界太近，无法做出准确预测。因此，我们希望找到一个判决边界，使得基于训练样本可以做出准确预测。

标识符

为了更方便的讨论SVM，引入新的标记方法。对于二分类问题中的标签y和特征x，我们令$y \in {-1,1}$来表示类的标签，不像之前的线性分类器那样使用$\theta$向量，这里使用参数$w,b$，分类器如下：

$h_{w,b}(x)=g(w^{T}x+b)$

式中的$b$相当于之前的$\theta_{0}$，$w$相当于$[\theta_{1},...,\theta_{n}]^{T}$。并且当$z \geq 0$时有$g(z)=1$，$z < 0$时有$g(z)=0$

函数和几何间隔

定义$(w,b)$的函数间隔：

$\hat {\gamma }^{(i)}=y^{(i)}(w^{T}x+b) $

如果$y^{(i)}=1$，若要函数间隔较大，则需要$w^{T}x+b$是一个较大的正数。

对于以上给出的$g$，当我们将$w$变为$2w$，$b$变为$2b$时，$g(w^{T}x+b)$变为$g(2w^{T}x+2b)$，这并不会改变$h_{w,b}(x)$，因为其取决于$w^{T}x+b$的符号而不是幅度。因此我们可以任意的增大函数间隔。

直观来看，引入一些正则化条件可能是有意义的，比如$\left \| w \right \|_{2}=1$，则$(w,b)$变为$(w/\left \| w \right \|_{2},b/\left \| w \right \|_{2})$。

给定训练集$S={(x^{(i)},y^{(i)});i=1,...,m}$，对独立的样本定义关于$(w,b)$的在$S$中最小的间隔函数(个人理解是所有样本点到判决边界的最小距离)：

$\hat {\gamma } = \underset{i=1,...,m}{min}\hat {\gamma }^{(i)}$

接下来讨论几何间隔：

如上图，$(w,b)$对应的判决边界如图所示。$w$与分割超平面正交。A点代表标签为$y^{(i)}=1$的$x^{(i)}$的输入，该点到判决边界的距离为$\gamma^{(i)}$，以线段AB表示。

那么如何计算$\gamma^{(i)}$的值呢？$w/||w||$是与w同方向的一个单位向量。既然A点表示$x^{(i)}$，那么我们可以发现B点可以由$x^{(i)}-\gamma^{(i)} \cdot w/||w||$表示，示意图如下：

对于所有在判决边界上的点x都有$w^{T}x+b=0$，因此：

$W^{T}(x^{(i)}-\gamma^{(ii)}\frac{w}{||w||})+b=0$

解得：

$w^{T}(x^{(i)}-\gamma^{(i)} \frac{w}{||2||})+b=0$

$w^{T}x^{(i)}+b=w^{T}\gamma^{(i)} \frac{w}{||w||}$

因为$v^{(i)}$是一个数值，$w$是一个列向量，则：

$w^{T}x^{(i)}+b=\gamma^{(i)} w^{T}\frac{w}{||w||}$

$w^{T}x^{(i)}+b=\gamma^{(i)} ||w||$

这是A点在y=1的一侧时的计算结果，更通用的公式如下：

最优间隔分类器

给定训练样本集，从之前的讨论可以看出我们想要找到一个间隔最大的判决边界。

提出以下最优问题：

我们希望找到一个最大的 $\gamma$使其满足对于所有训练样本的函数间隔都不小于该$\gamma$值。$||w||=1$用于约束，保证函数间隔等于几何间隔，因此我们也可以保证几何间隔不小于$\gamma$。

但是以上公式由于$||w||=1$的约束，变成非凸函数，难以求解。因此作以下变换：

以上公式依然是非凸函数，没有现成的算法可以解决这个最优化问题。

之前我们说过$w,b$乘以一个常数不会改变计算结果，同时相当于函数间隔乘以一个常数。因此，我们可以改变$w,b$的尺度，使：

$\hat {\gamma}=1$。

因此最大化$\hat {\gamma}/||w||=1/||w||$等同于最小化$||w||^{2}$，最优化问题变成如下：

上面的公式是一个凸二次目标且仅有一个线性约束，它的结果就可以得到最优化间隔分类器。这个最优化问题可以使用商业二次规划代码求解。

拉格朗日对偶

接下来我们讨论解决受约束的最优化问题。

考虑一下问题：

构造拉格朗日函数：

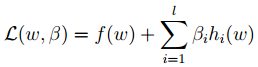
这里$\beta_{i}$为拉格朗日算子。令其偏导为0：

然后解出$w,\beta$。

接下来考虑优先优化问题：

后面的内容比较复杂，暂时省略。

最优间隔分类器

前面为了寻找最有间隔分类器I，我们提出以下优化问题：

约束条件写成如下：

从KKT条件（上节内容）的值，只有函数间隔为1的线性约束式前面的系数$a_{i}>0$，也就是这些约束式$g_{i}(w)=0$。

下图，实线表示最大间隔分割超平面：

虚线上的点都是函数间隔为1的点，那么他们前面的系数$a_{i}>0$，其他点都是$a_{i}=0$。这三个点称作支持向量。支持向量的数目应该远远小于训练样本数目。

使用拉格朗日重新构造最优化问题：

按照对偶问题进行求解：

首先求$\iota (w,\alpha,\beta)$的最小值，固定$a_{i}$，最小值只与$w,b$有关。对$w$求偏导，令其偏导为0：

以上求导使用到以下求导公式：

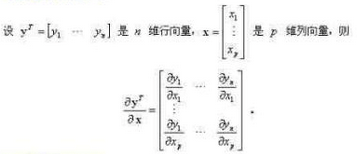
具体参考以下链接：

矩阵求导公式（1）矩阵求导公式（2）

得：

对b求偏导：

得到以下三个式子：

将第二个带入到第一个得：

结合第三个式子可得：

最小化含有参数$w,b$的$\iota $问题转化为下面的对偶最优问题：

前面得到以下公式：

因此当我们预测时会计算$w^{T}x+b$，在这里可以写成：

也就是说，以前新来的要分类的样本首先根据w和b做一次线性运算，然后看求的结果是大于0还是小于0,来判断正例还是负例。现在有了$a_{i}$，我们不需要求出w，只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说，与前面所有的样本都做运算是不是太耗时了？其实不然，我们从KKT条件中得到，只有支持向量的$a_{i}>0$，其他情况$a_{i}=0$。因此，我们只需求新来的样本和支持向量的内积，然后运算即可。