动态规划——活动选择问题

一个递归解

　　设c[i][j]为S_ij中最大兼容子集中的活动数目，当S_ij为空集时，c[i][j]=0；当S_ij非空时，若a_k在S_ij的最大兼容子集中被使用，则则问题S_ik和S_kj的最大兼容子集也被使用，故可得到c[i][j] = c[i][k]+c[k][j]+1。

当i≥j时，S_ij必定为空集，否则S_ij则需要根据上面提供的公式进行计算，如果找到一个a_k，则S_ij非空（此时满足f_i≤s_k且f_k≤s_j），找不到这样的a_k，则S_ij为空集。

c[i][j]的完整计算公式如下所示：

 

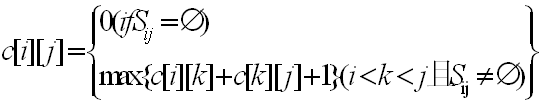
最优解计算过程

　　根据递归公式，采用自底向下的策略进行计算c[i][j]，程序实现如下所示：

#include <iostream>
using namespace std;

const int N = 11;
int s[N+2]= {-1,1,3,0,5,3,5,6,8,8,2,12,65535};
int f[N+2]= {-1,4,5,6,7,8,9,10,11,12,13,14,65535};

//trace[i][j]跟踪子问题S(i,j)每次最优时的划分
int trace[N+2][N+2];

//dp[i][j]表示子问题S(i,j)的最多兼容活动数
int dp[N+2][N+2];

/*S(i,j)={ak,fi<=sk<fk<=sj}表示在活动ai结束之后，在aj开始之前的活动集，则整个问题空间可表示为S(0,n+1),
*其中添加活动a0和an+1，s0=f0=0,sn+1=fn+1=2^32-1
*根据dp[i][j]的含义,假设S(i,j)中不包含任何的活动序列(即满足S(i,j)定义的活动不存在)，则dp[i][j]=0；
*否则，假设ak时S(i,j)中存在的一个兼容活动,那
*么这里存在问题S(i,j)的最优子结构:S(i,k)和S(k,j).
*根据上面叙述，可以定义问题的递归解结构:
*dp[i][j]=0,如果S(i,j) =NULL
*dp[i][j]=max{dp[i][k]+dp[k][j]+1},i<k<j
*/
void dp_solve()
{
    int i =0;
    int j = 0;
    int l = 0;
    int k = 0;
    for(i=1; i<=N+1; i++)
        for(j=1; j<=N+1; j++)
            if(i==j)
                dp[i][j]=1;
    dp[0][0] = dp[N+1][N+1] = 0;
    for(l=1; l<N+2; l++)
        for(i=0; i+l<N+2; i++)
        {
            j=i+l;
            if(j<N+2)
            {
                dp[i][j] = 0;
                trace[i][j] = 0;
                for(k=i+1; k<j; k++)
                {
                    if(f[i]<=s[k] && f[k]<=s[j])//寻找是dp[i][k]+dp[k][j]最大的值
                    {
                        if(dp[i][k] + dp[k][j]+1 > dp[i][j])
                        {
                            dp[i][j] = dp[i][k]+dp[k][j] +1;
                            trace[i][j] = k;
                        }
                    }
                }
            }
        }
}
void print(int i,int j)
{
    int k =0;
    if(trace[i][j]==0)
        return;
    k = trace[i][j];
    cout << k << "  ";
    print(i,k);
    print(k,j);
}

int main()
{
    dp_solve();
    print(0,N+1);
    cout<<endl;
    int i,j;
    cout<<"dp matrix:"<<endl;
    for(i=0; i<=N+1; i++)
    {
        for(j=0; j<=N+1; j++)
            cout<<dp[i][j]<<" ";
        cout<<endl;
    }
    cout<<"trace matrix:"<<endl;
    for(i=0; i<=N+1; i++)
    {
        for(j=0; j<=N+1; j++)
            cout<<trace[i][j]<<" ";
        cout<<endl;
    }
    return 0;
}

运行结果：