第十五章 动态规划——最优二叉搜索树

　1、前言：

　　接着学习动态规划方法，最优二叉查找树问题。二叉查找树参考http://www.cnblogs.com/Anker/archive/2013/01/28/2880581.html。如果在二叉树中查找元素不考虑概率及查找不成功的情况下，可以采用红黑树或者平衡二叉树来搜索，这样可以在O(lgn)时间内完成。而现实生活中，查找的关键字是有一定的概率的，就是说有的关键字可能经常被搜索，而有的很少被搜索，而且搜索的关键字可能不存在，为此需要根据关键字出现的概率构建一个二叉树。比如中文输入法字库中各词条（单字、词组等）的先验概率，针对用户习惯可以自动调整词频——所谓动态调频、高频先现原则，以减少用户翻查次数，使得经常用的词汇被放置在前面，这样就能有效地加快查找速度。这就是最优二叉树所要解决的问题。

2、问题描述

　   给定一个由n个互异的关键字组成的有序序列K={k₁<k₂<k₃<,……,<k_n}和它们被查询的概率P={p₁,p₂,p₃,……,p_n}，要求构造一棵二叉查找树T，使得查询所有元素的总的代价最小。对于一个搜索树，当搜索的元素在树内时，表示搜索成功。当不在树内时，表示搜索失败，用一个“虚叶子节点”来标示搜索失败的情况，因此需要n+1个虚叶子节点{d₀<d₁<……<d_n}，对于应d_i的概率序列是Q={q₀,q₁,……,q_n}。其中d₀表示搜索元素小于k₁的失败结果，d_n表示搜索元素大于k_n的失败情况。d_i（0<i<n）表示搜索节点在k_i和k_(i+1)之间时的失败情况。因此有如下公式：

　　由每个关键字和每个虚拟键被搜索的概率，可以确定在一棵给定的二叉查找树T内一次搜索的期望代价。设一次搜索的实际代价为检查的节点个数，即在T内搜索所发现的节点的深度加上1。所以在T内一次搜索的期望代价为：

需要注意的是：一棵最优二叉查找树不一定是一棵整体高度最小的树，也不一定总是把最大概率的关键字放在根部。

（3）动态规划求解过程

1）最优二叉查找树的结构

　　如果一棵最优二叉查找树T有一棵包含关键字k_i，……，k_j的子树T'，那么这棵子树T’对于对于关键字k_i，……k_j和虚拟键d_i-1，……，d_j的子问题也必定是最优的。

2）一个递归解

　　定义e[i,j]为搜索一棵包含关键字ki，……，kj的最优二叉查找树的期望代价，则分类讨论如下：

当j=i-1时，说明此时只有虚拟键d_i-1，故e[i,i-1] = q_i-1

当j≥i时，需要从k_i，……，k_j中选择一个跟k_r，然后用关键字k_i，……，k_r-1来构造一棵最优二叉查找树作为左子树，用关键字k_r+1，……，k_j来构造一棵最优二叉查找树作为右子树。定义一棵有关键字k_i，……，k_j的子树，定义概率的总和为：

因此如果k_r是一棵包含关键字k_i，……，k_j的最优子树的根，则有：

 

故e[i,j]重写为：

最终的递归式如下：

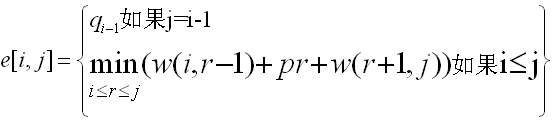
3）计算一棵最优二叉查找树的期望搜索代价

　　将e[i,j]的值保存到一个二维数组e[1..1+n,0..n]中，用root[i,j]来记录关键字ki，……，kj的子树的根，采用二维数组root[1..n,1..n]来表示。为了提高效率，防止重复计算，需要个二维数组w[1..n+1,0...n]来保存w(i,j)的值，其中w[i,j] = w[i,j-1]+p_j+q_j。数组给出了计算过程的伪代码：

OPTIMAL_BST(p,q,n)
    for i=1 to n+1    //初始化e和w的值
       do e[i,i-1] = qi-1;
          w[i,i-1] = qi-1;
     for l=1 to n
        do for i=1 to n-l+1
                  do j=i+l-1;
                       e[i,j] = MAX;
                       w[i,j] = w[i,j-1]+pj+qj;
                       for r=i to j
                               do t=e[i,r-1]+e[r+1,j]+w[i,j]
                                    if t<e[i,j]
                                         then e[i,j] = t;
                                              root[i,j] = r;
return e and root;

4）构造一棵最优二叉查找树

　　根据地第三步中得到的root表，可以递推出各个子树的根，从而可以构建出一棵最优二叉查找树。从root[1,n]开始向下递推，一次找出树根，及左子树和右子树。

4、编程实现

　　针对一个具体的实例编程实现，现在有5个关键字，其出现的概率P={0.15，0.10，0.05，0.10，0.20}，查找虚拟键的概率q={0.05，0.10，0.05，0.05，0.05，0.10}。采用C++语言是实现如下：

#include<iostream>
using namespace std;

const int N=5;
const int MAX=9999999;
float p[N+1]={0,0.15,0.10,0.05,0.1,0.20};
float q[N+1]={0.05,0.10,0.05,0.05,0.05,0.10};

float e[N+2][N+1];
int root[N+1][N+1];
float w[N+2][N+1];

void optimal_bst_search_tree(float p[],float q[],int n)
{
    int i;
    for(i=1;i<=n+1;i++)
    {
        e[i][i-1]=q[i-1];
        w[i][i-1]=q[i-1];
    }
    int l,j,r;
    for(l=1;l<=n;l++)
    {
        for(i=1;i<=n-l+1;i++)
        {
            j=i+l-1;
            e[i][j]=MAX;
            w[i][j]=w[i][j-1]+p[j]+q[j];
            for(r=i;r<=j;r++)
            {
                double t=e[i][r-1]+e[r+1][j]+w[i][j];
                if(t<e[i][j])
                {
                    e[i][j]=t;
                    root[i][j]=r;
                }
            }
        }
    }
}

void print_root()
{
    int i,j;
    cout<<"各子树的根："<<endl;
    for(i=1;i<=N;i++)
    {
        for(j=1;j<=N;j++)
            cout<<root[i][j]<<" ";
        cout<<endl;
    }
}

void construct_optimal_bst(int i,int j)
{
    if(i<=j)
    {
        int r=root[i][j];
        cout<<r<<" ";
        construct_optimal_bst(i,r-1);
        construct_optimal_bst(r+1,j);
    }
}
void print_bst(int i,int j)
{
    if(i==1&&j==N)
        cout<<"root is "<<root[i][j]<<endl;
    if(i<j)
    {
        int r=root[i][j];
        if(i!=r)
            cout<<"left child root "<<root[i][r-1]<<endl;
        print_bst(i,root[i][j]-1);
        if(j!=r)
            cout<<"right child root "<<root[r+1][j]<<endl;
        print_bst(root[i][j]+1,j);
    }
}
int main()
{
    optimal_bst_search_tree(p,q,N);
    print_root();
    cout<<"构造的最优二叉树："<<endl;
    construct_optimal_bst(1,5);
    cout<<endl;
    print_bst(1,5);
}

运行结果：